概率论 重要的随机变量

离散分布

two-point 0-1 分布

抛一个硬币，硬币向上的概率是 p，若向上为1，向下为0，这个变量就是0-1分布。

k	0	1
\(P(X=k)\)	\(1-p\)	\(p\)

\[E(X) = p \]

\[D(X) = p(1-p) \]

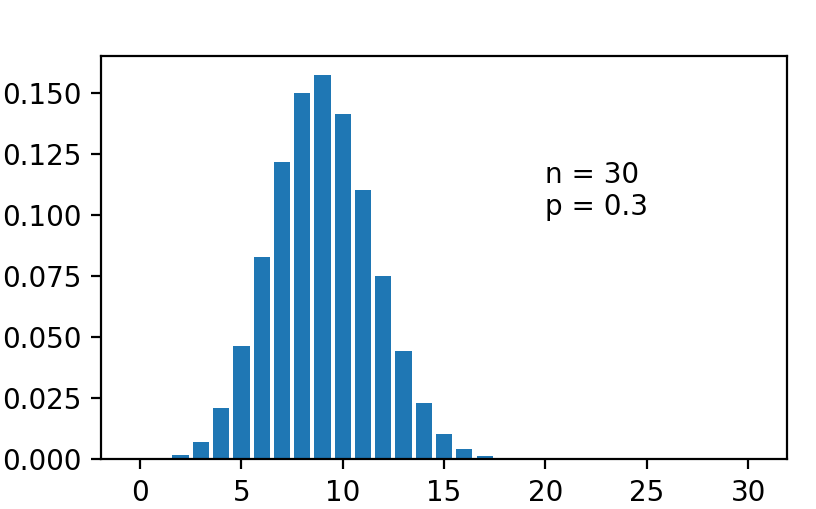
Bernoulli 二项分布

现有一个硬币，抛 n 次，如果每次硬币向上的概率是 p，那么记 n 次实验里硬币向上发生的次数 X 为二项分布，又叫伯努利分布，写作\(X \sim B(n, p)\)。

\[P(X=k) = \C_n^k\ p^k(1-p)^{n-k} \]

\[E(X) = np \]

\[D(X) = np(1-p) \]

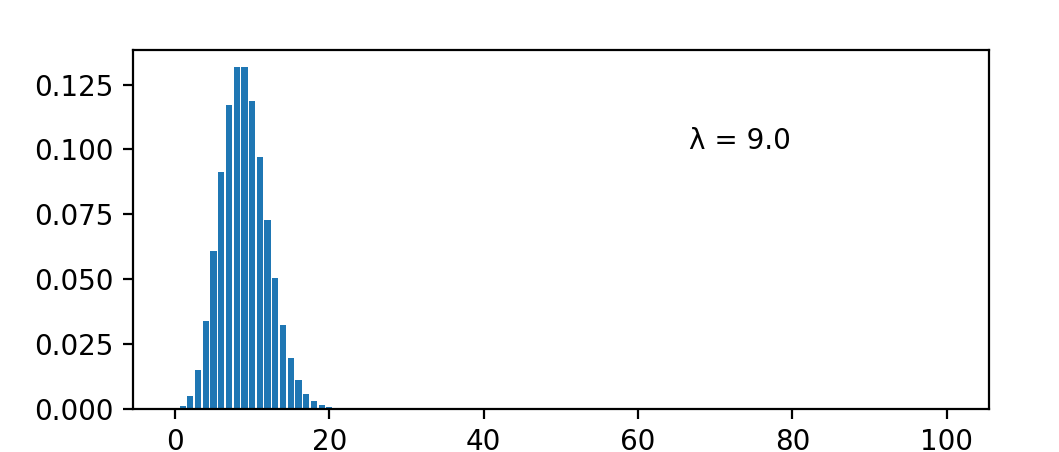
Poisson 泊(bó)松分布

在二项分布里，记 \(\lambda = np\)，那么

\[P(X=k) = \C_n^k\ p^k(1-p)^{n-k}=\frac{n(n-1)...(n-k+1)}{k!}(\frac λn)^k(1-\frac λn)^{n-k} \]

\[=((1-\frac 1n)...(1-\frac {k-1}n))(\frac {λ^k}{k!})(1-\frac λn)^{{\frac λn}(-λ)(1-\frac kn)} \]

那么\(n\to \infty\)时，\(P(X=k) = e^{-λ}\frac {λ^k}{k!}\)，这就是泊松分布，记作\(P(λ)\)。他是二项分布在 n 足够大时的近似。

\[E(X) = λ \]

\[D(X) = λ \]

比如说，一个商店开放一个小时，任何时候来人都是等可能的。如果已知每分钟出现一个人的概率是 p，没有人的概率就是 1-p，那么来的人数量这就是一个二项分布\(B(60, p)\)。

但是一分钟有可能出现多个人，为了更加精确分成30秒一算，30秒出现一个人的概率就是\(\frac p2\)，来的人数量变成了\(B(120, \frac p2)\)；分成1秒钟一算，那就是\(B(3600, \frac p{60})\)，随着 n 走向无穷细分，np 却是个定值，他可以用来表示概率的大小，最终的分布是\(P(60p)\)。

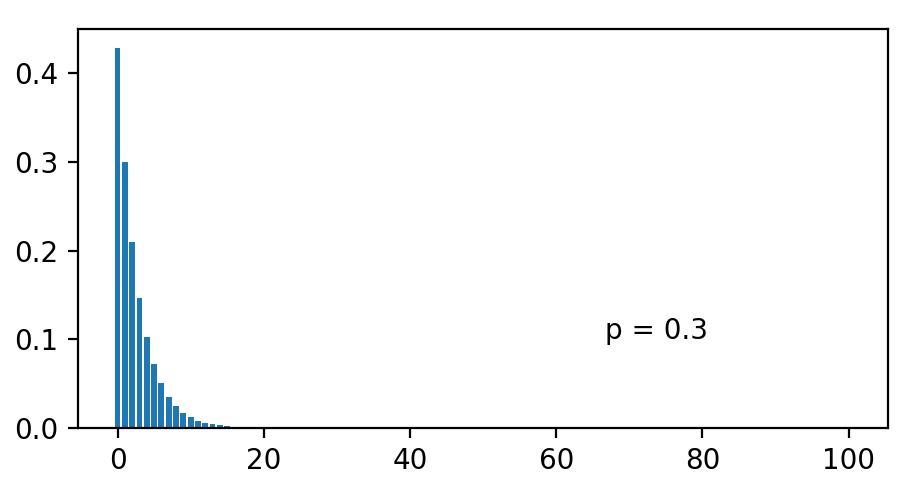
Geometric 几何分布

现有一个硬币，如果每次硬币向上的概率是 p，那么一直抛硬币直到硬币向上。记第一次出现硬币向上时所抛硬币的次数为几何分布，写作\(X \sim G(p)\)。

\[P(X=k) = p(1-p)^{k-1} \]

\[E(X) = \frac 1p \]

\[D(X) = \frac {1-p}{p^2} \]

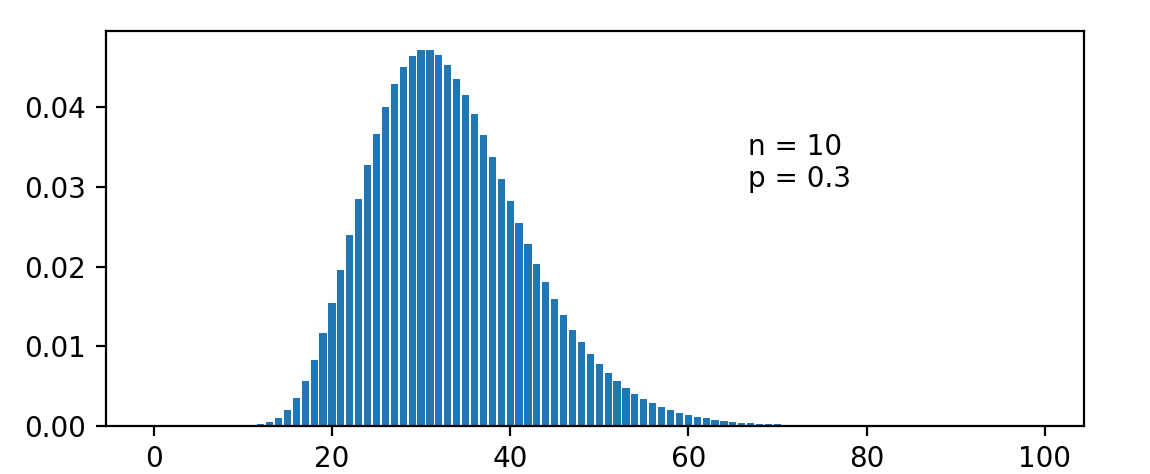
Pascal 负二项分布

现有一个硬币，如果每次硬币向上的概率是 p，那么一直抛硬币直到硬币向上出现了 n 次。记此时所抛硬币的次数为负二项分布，写作\(X \sim NB(n, p)\)。显然几何分布就是 n = 1 的情况。

\[P(X=k) = \C_{n-1}^{k-1}\ p^n(1-p)^{k-n}\ \ (k\ge n) \]

\[E(X) = \frac np \]

\[D(X) = \frac {n(1-p)}{p^2} \]

Hypergeometric 超几何分布

N 个产品中有 M 个不合格品，现在不放回抽取 n 个，那么次品的数量就是一个超几何分布，记作\(X \sim H(n, M, N)\)。

\[P(X=k) = \frac{\C_M^k\C_{N-M}^{n-k}}{\C_N^n}\ \ (\max(0,n-N+M)\le k\le \min(n,M)) \]

\[E(X) = n\frac MN \]

\[D(X) = n\frac MN(1-\frac MN)(\frac {N-n}{N-1}) \]

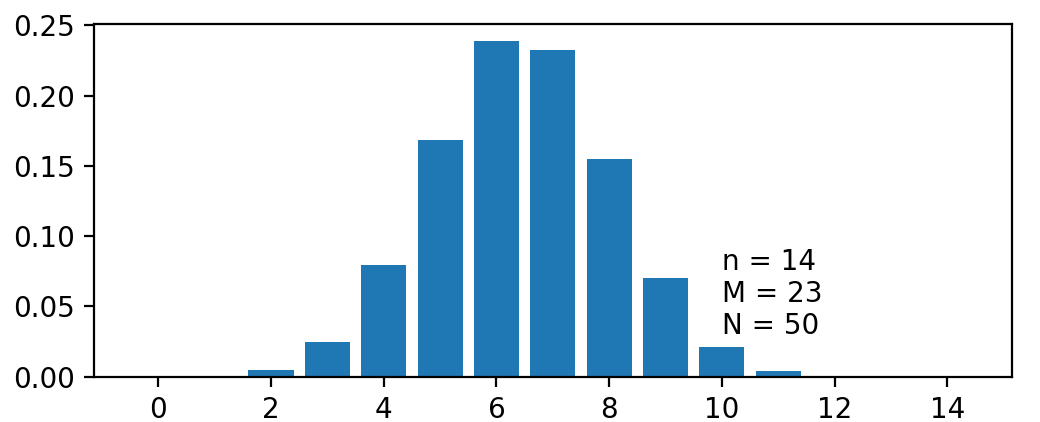
当 N 相比 n 非常大时，放回抽取和不放回抽取近似相等，此时可以近似为二项分布\(B(n, \frac MN)\)。

连续分布

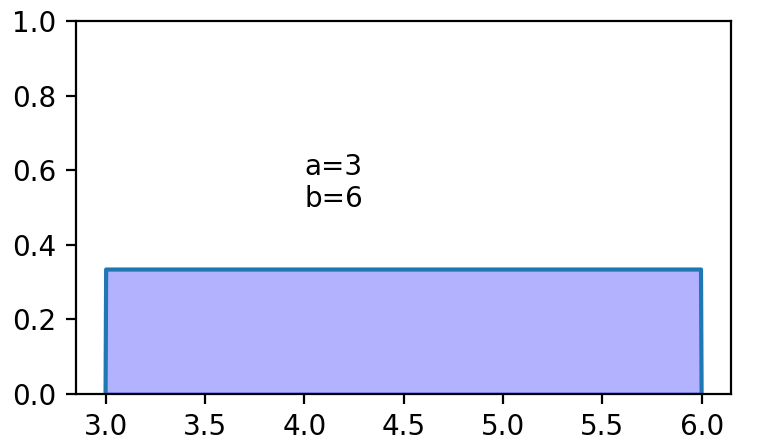
Uniform 均匀分布

均匀分布在区间\([a,b]\)的分布就是均匀分布，写作\(X \sim U(a, b)\)。

\[f(x)=\frac 1{b-a}\ \ (a<x<b) \]

\[E(X) = \frac{a+b}2 \]

\[D(X) = \frac {(b-a)^2}{12} \]

Exponential 指数分布

指数分布写作\(X \sim E(λ)\)。

\[f(x)=λe^{-λx}\ \ (x>0) \]

\[E(X) = \frac 1λ \]

\[D(X) = \frac 1{λ^2} \]

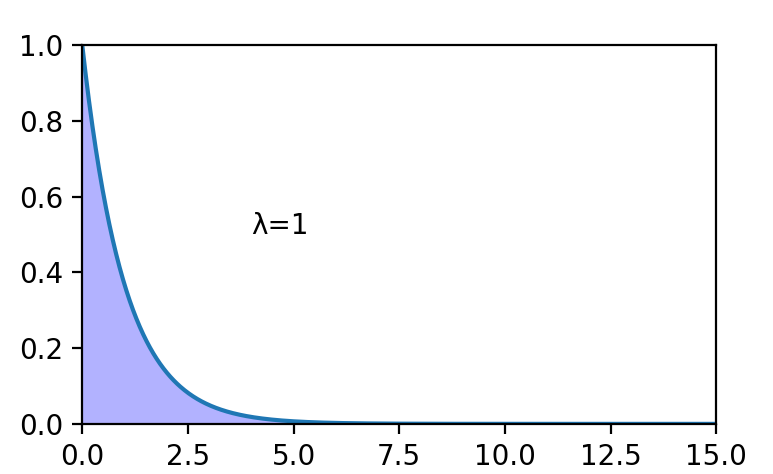
指数分布和泊松分布有密切关系。对于一个随时可能来人的商店，一小时内的来客数量是泊松分布，而来客和上一个来客出现的时间间隔就是一个指数分布。假设现在来了一个人，下一个人在 t 分钟后出现，中间 t 分钟没有出现人，概率就是\(P(P(tp) = 0)=e^{-tp}\)，由此可见，接下来一分钟出现人概率是\(e^{-p}\)，两分钟才出现就是\(e^{-2p}\)，这个数会迅速减小。

指数分布还有无记忆性：\(P(X>t+s|X>s)=P(X>t)\)，如果过了一分钟下一个人没有出现，他再过一分钟出现的概率还是 \(e^{-p}\)。

指数分布也是几何分布的一种渐进。他们的图像十分相近，一个是离散分布而另一个是连续分布。事实上指数分布正是几何分布的一种逼近。\(G(p)\)代表每次发生概率为 p 的事件第一次发生的次数，假设上一个那个均匀来人的商店里每分钟来人的概率是 p ，把一小时分成 60 段，那么第一次出现人的时间段就是\(G(p)\)，如果把半分钟作为单位时间分为120段，答案就变成了\(\frac {G(p)}2\)；要继续细分，我们要令单位时间内发生事件的概率为“λ”（在这个例子里\(λ = p\)），当分段n 足够大的时候：

\[P(X\le k)=\Sigma_1^k P(X=i)=\Sigma_1^k (1-\frac λn)^{i-1}\frac λn \]

那么\(n\to \infty\)时，由等比数列求和公式，最终可以求得\(P(X\le k) = 1 - e^{-λk}\)，再求导就得到的指数分布。

Normal 正态分布

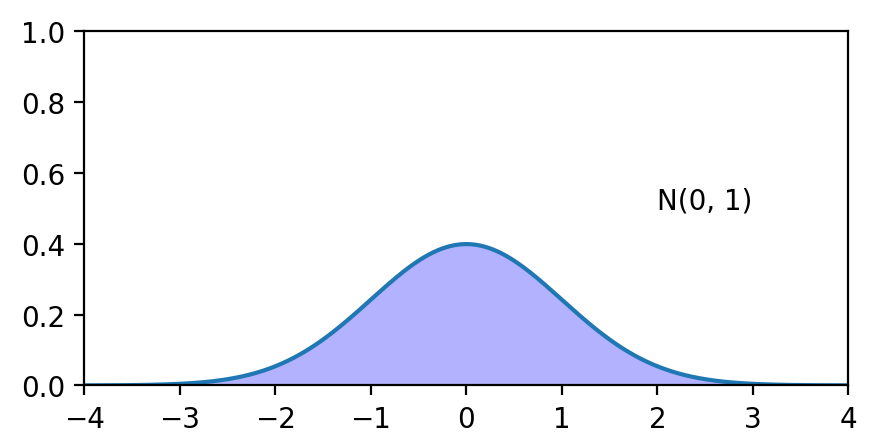
正态分布是“分布之王”，非常重要的分布，是我们构造“中间高两边低”这样的分布的基本模型。他最早来源于二项分布的一种渐进，正态分布记作\(N(μ, σ^2)\)，两个参数直接代表期望和方差。

\[f(x)=\frac 1{\sqrt{2π}σ}e^{-\frac{(x-μ)^2}{2σ^2}} \]

\[φ(x)=\frac 1{\sqrt{2π}}e^{-\frac{x^2}{2}} \]

\(φ(x)\)即标准正态分布\(N(0,1)\)，他的积分（分布函数）记作大 phi（\(Φ(x)\)）。由密度表达式所有正态分布都可以线性转化为标准正态分布，所以标准正态分布就显得尤为重要。

\[Y\sim N(μ, σ^2),\ X\sim N(0,1)\to Y=\frac {X-\mu}{\sigma} \]