一维的孤立森林算法

孤立森林（Isolation Forest）算法，是一种用于排查异常数据的算法。它的名字听上去十分高端，感觉不可能在OI里用到，事实上也的确没有听说过这方面的题，而我接触这个算法是因为数学建模大赛时小组中发现这个算法可用，然后就去学了一下。本身要感性理解它并不困难，不过打起来还是有点繁琐。当时只用到了弱化再弱化的一维的情况，所以总结一下一维数据的做法，感性理解即可。

---

有一个数列保存的一些计算数据，大部分正常，少部分是错误的，现在要排除出过于离谱的数据。

我们把数据放到数轴上，容易发现大部分数据都是堆在一起的，只有少部分数据里中心点较远。

那么我们在数列的最大值和最小值之间随机选取一个数作为中点，把数列一分为二。

接下来递归进入左右两边继续同样的操作，将值域不断分割。显然每个区间包含的点数是越来越少的，最终会变成1，这个时候就不再分割，记录下这个点递归了多少层，然后return。

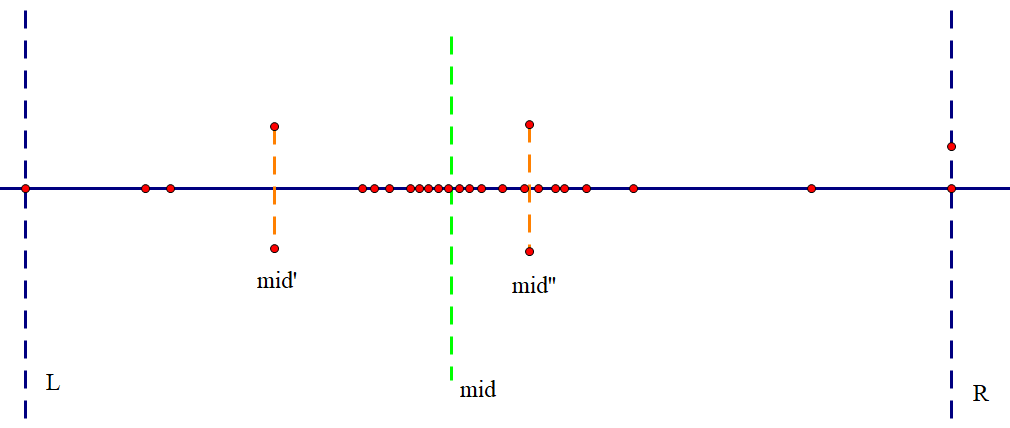
那么这些区间就会形成一个搜索树，而越是离中心地区远的点就越容易提早被孤立出来，它们的深度就越浅，因此以深度就可以大致判断那些数据是错误的。当然跑一次的偶然概率太大，我们可以多跑几次（一般100次），给每一个点的深度求一个平均值以减小误差。

但是这还远远没有完，如果出现“异常数据也抱团”和“正常异常数据太接近”的情况，孤立森林的误差就会大大增加， 所以我们应该减小数据的规模来避免它，每次取\(\psi\)个数跑IForest即可，而这个\(\psi\)一般取常数256。

同时，当分割已经分割出很多异常数据时，仍然“抱团的数据”基本上可以视为正常，我们规定一个最大深度\(Hmax = ceil(log_2 \psi) = 8\)（根节点深度是0），达到最大深度时，即使开没有分割完毕也不再继续下分。

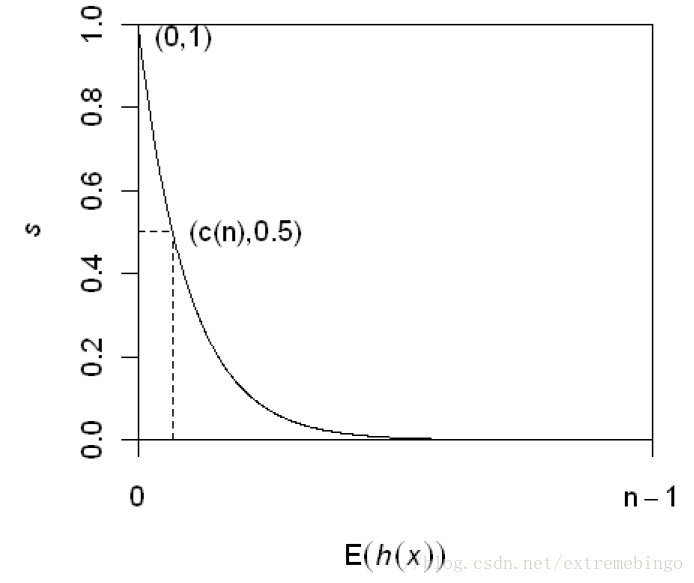
最后我们得到每一个点相对准确的平均深度\(h_x\)，可以用这个来计算“异常分数值”\(s(x, \psi)\)，当\(\psi\)固定时可以按照下式计算:

\[s(x, \psi) = 2 ^ {\frac {h_x} {c(\psi)}} \]

其中\(c(i) = 2H(i-1)-\frac {2(i-1)} i,\ H(i) = ln(i)+0.577215665\)，这个c值因为\(\psi\)是常数可以直接计算出。

现在我们得到了所有s值，s值越接近1的就可以认为越异常。这里放上CSDN的一张图：

// 注意生成随机数不要写错 
inline d64 rand(d64 l, d64 r) {
	return rand() / 32768.0 * (r - l + 1) + l;
}
inline int rand(int l, int r) {
	return rand() * rand() % (r - l + 1) + l;
}

unordered_map <double, int> HASH;

int sc[MAX], uc[MAX];
double b[MAX], c[MAX];

void DFS(d64 l, d64 r, int dep)
{
	int xl = lower_bound(b, b+256, l) - b;
	int xr = upper_bound(b, b+256, r) - b;
	//找到本区间最靠左， 最靠右的点编号 
	
	if (xr - xl <= 1 || dep == 8) // 如果只剩一个或者到达深度上限 
	{ 
		for (int i = xl; i < xr; i++)
		{
			// 统计这个数被抽到的次数和深度总和，计算平均数 
			sc[HASH[b[i]]] += dep;
			uc[HASH[b[i]]] ++;
		}return;
	}

	double mid = rand(b[xl], b[xr-1]);// 随机断开，递归分治 
	DFS(l, mid, dep+1);
	DFS(mid, r, dep+1);
}

void Iforest(int l, int r)
{
	for (int i = 1; i <= N; i++)
		HASH[b[i]] = i, ord[i] = i;
	for (int T = 1; T <= 900; T++) // 算法运行次数 
	{
		for (int i = 1; i <= N; i++)
			swap(b[rand(1, N)], b[rand(1, N)]);
		// 随机打乱序列 
		
		sort(b + 1, b + 257); // 选取前256个数跑算法 
		DFS(b[1], b[256], 0);
	}
	for (int i = 1; i <= N; i++) 
	{
		d64 avee = (d64)sc[i] / uc[i];
		c[i] = pow(2, -avee / 12.5237); // 这里的c就是刚才的s值
	}
	sort(ord + 1, ord + N + 1, [](int x, int y) {return c[x] > c[y];});
	for (int i = 1; i <= N; i++)
		rank[ord[i]] = i;
	// 记录每个点的排名，这里选取了c值最大的2%作为异常数据 
	for (int i = l; i <= r; i++)
		puts(rank[i] * 50 <= N ? "Abnormal" : "Normal");
}