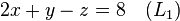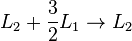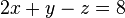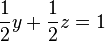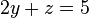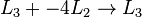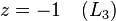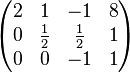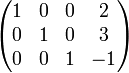原文出自:http://zh.wikipedia.org/wiki/%E9%AB%98%E6%96%AF%E6%B6%88%E5%8E%BB%E6%B3%95
例子
高斯消元法可用来找出下列方程组的解或其解的限制:
这个算法的原理是:
首先,要将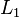 以下的等式中的
以下的等式中的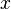 消除,然后再将
消除,然后再将 以下的等式中的
以下的等式中的 消除。这样可使整个方程组变成一个三角形似的格式。之后再将已得出的答案一个个地代入已被简化的等式中的未知数中,就可求出其余的答案了。
消除。这样可使整个方程组变成一个三角形似的格式。之后再将已得出的答案一个个地代入已被简化的等式中的未知数中,就可求出其余的答案了。
在刚才的例子中,我们将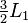 和
和 相加,就可以将
相加,就可以将 中的
中的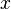 消除了。然后再将
消除了。然后再将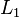 和
和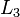 相加,就可以将
相加,就可以将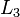 中的
中的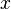 消除。
消除。
我们可以这样写:
结果就是:
现在将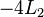 和
和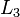 相加,就可将
相加,就可将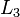 中的
中的 消除:
消除:
其结果是:
这样就完成了整个算法的初步,一个三角形的格式(指:变量的格式而言,上例中的变量各为3,2,1个)出现了。
第二步,就是由尾至头地将已知的答案代入其他等式中的未知数。第一个答案就是:
然后就可以将 代入
代入 中,立即就可得出第二个答案:
中,立即就可得出第二个答案:
之后,将 和
和 代入
代入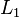 之中,最后一个答案就出来了:
之中,最后一个答案就出来了:
就是这样,这个方程组就被高斯消元法解决了。
这种算法可以用来解决所有线性方程组。即使一个方程组不能被化为一个三角形的格式,高斯消元法仍可找出它的解。例如在第一步化简后, 及
及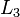 中没有出现任何
中没有出现任何 ,没有三角形的格式,照着高斯消元法而产生的格式仍是一个行梯阵式。这情况之下,这个方程组会有超过一个解,当中会有至少一个变量作为答案。每当变量被锁定,就会出现一个解。
,没有三角形的格式,照着高斯消元法而产生的格式仍是一个行梯阵式。这情况之下,这个方程组会有超过一个解,当中会有至少一个变量作为答案。每当变量被锁定,就会出现一个解。
通常人或电脑在应用高斯消元法的时候,不会直接写出方程组的等式来消去未知数,反而会使用矩阵来计算。以下就是使用矩阵来计算的例子:
跟着以上的方法来运算,这个矩阵可以转变为以下的样子:
这矩阵叫做“行梯阵式”。
最后,可以利用同样的算法产生以下的矩阵,便可把所得出的解或其限制简明地表示出来:
最后这矩阵叫做“简化行梯阵式”,亦是高斯-约当消元法指定的步骤。
[编辑] 其他应用
[编辑] 找出逆矩阵
高斯消元法可以用来找出一个可逆矩阵的逆矩阵。设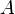 为一个
为一个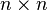 的矩阵,其逆矩阵可被两个分块矩阵表示出来。将一个
的矩阵,其逆矩阵可被两个分块矩阵表示出来。将一个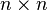 单位矩阵 放在
单位矩阵 放在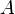 的右手边,形成一个
的右手边,形成一个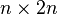 的分块矩阵
的分块矩阵![B = [A, I]](http://upload.wikimedia.org/wikipedia/zh/math/c/1/5/c158995cd304061dd28b5a1257f75618.png) 。经过高斯消元法的计算程序后,矩阵
。经过高斯消元法的计算程序后,矩阵 的左手边会变成一个单位矩阵
的左手边会变成一个单位矩阵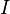 ,而逆矩阵
,而逆矩阵 会出现在
会出现在 的右手边。
的右手边。
假如高斯消元法不能将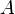 化为三角形的格式,那就代表
化为三角形的格式,那就代表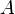 是一个不可逆的矩阵。
是一个不可逆的矩阵。
应用上,高斯消元法极少被用来求出逆矩阵。高斯消元法通常只为线性方程组求解。[2]
[编辑] 计出秩的基本算法
高斯消元法可应用在任何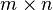 的矩阵
的矩阵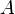 。在不可减去某数的情况下,我们都只有跳到下一行。以一个
。在不可减去某数的情况下,我们都只有跳到下一行。以一个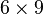 的矩阵作例,它可以变化为一个行梯阵式:
的矩阵作例,它可以变化为一个行梯阵式:
而矩阵中的 *' 是一些数字。这个梯阵式的矩阵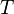 会有一些关于
会有一些关于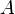 的资讯:
的资讯:
[编辑] 分析
高斯消元法的算法复杂度是O(n3);这就是说,如果系数矩阵的是n × n,那么高斯消元法所需要的计算量大约与n3成比例。
高斯消元法可以用在电脑中来解决数千条等式及未知数。不过,如果有过百万条等式时,这个算法会十分费时。一些极大的方程组通常会用迭代法来解决。亦有一些方法特地用来解决一些有特别排列的系数的方程组。
高斯消元法可用在任何域中。
高斯消元法对于一些矩阵来说是稳定的。对于普遍的矩阵来说,高斯消元法在应用上通常也是稳定的,不过亦有例外。[3]
[编辑] 虚拟码
高斯消元法的其中一种虚拟码:
i := 1
j := 1
while (i ≤ m and j ≤ n) do
Find pivot in column j, starting in row i:
maxi := i
for k := i+1 to m do
if abs(A[k,j]) > abs(A[maxi,j]) then
maxi := k
end if
end for
if A[maxi,j] ≠ 0 then
swap rows i and maxi, but do not change the value of i
Now A[i,j] will contain the old value of A[maxi,j].
divide each entry in row i by A[i,j]
Now A[i,j] will have the value 1.
for u := i+1 to m do
subtract A[u,j] * row i from row u
Now A[u,j] will be 0, since A[u,j] - A[i,j] * A[u,j] = A[u,j] - 1 * A[u,j] = 0.
end for
i := i + 1
end if
j := j + 1
end while
这个算法和之前谈及的有点儿不同,它由绝对值最大的部分开始做起,这样可以改善算法上的稳定性。将经过调换后的第一列作为起点,这算法由左至右地计算。每作出以下两个步骤,才跳到下一列:
- 定出每列的最后一个非0的数,将每行的数字除以该数,使到每行的第一个数成为1;
- 将每行的数字减去第一行的第一个数的某个倍数。
所有步骤完成后,这个矩阵会变成一个行梯阵式,再用代入法就可解决这个方程组。