对比python学julia（第二章）--（第三节）玫瑰曲线—数学之美

3.1.问题描述

　　在数学世界中有一些美丽的曲线图形，有螺旋线、摆线、双纽线、蔓叶线且、心脏线、渐开线、玫瑰曲线、蝴蝶曲线…… 这些形状各异、简有繁别的数学曲线图形为看似枯燥的数学公式披上精彩纷呈的美丽衣裳。

　　在数学曲线的百花园中，玫瑰曲线算得上个中翘楚，它的数学方程简单，曲线变化众多，根据参数的变化能展现出姿态万千的优美形状。玫瑰曲线可用极坐标方程表示为

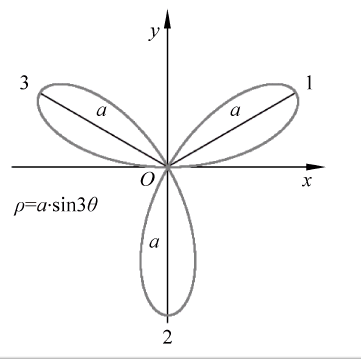
图一、三叶玫瑰曲线

ρ=a∗sinθ

　　也可以用参数方方程表示为

$$\{\begin{array}{c}x=a\ast \text{sin}n\theta \ast \text{cos}\theta \\ y=a\ast \text{sin}n\theta \ast \text{sin}\theta \end{array}$$

　　其中，参数a控制叶子的长度；参数n控制叶子的数量，并影响曲线闭合周期。 当n为奇数时，玫瑰曲线的叶子数为n，闭合周期为 π，即参数 的取值范围为0~π ，才能使玫瑰曲线闭合为完整形图。当n为偶数时，玫瑰曲线的叶子数为2n，，闭合周期为 2π ，即参数 的取值范围为0~2π，如图所示，这是方程 ρ=a∗sinθ对应的三叶玫瑰曲线图形。

　　请编写程序，在海龟绘图窗口 中绘制一幅三叶玫瑰曲线的图形。

　　

 

 

 3.2.问题描述

　　在数学世界中，像玫瑰曲线这样美丽的曲线图形实际上是由简单的函数关系生成的。通过利用曲线函数的参数方程，可以在平面直角坐标系中方便地绘制出它们的图形。

　　假如要利用玫瑰曲线的参数方程绘制三叶玫瑰曲线，则参数n的值可以设定为3，参数a的值可以设定叶子的长度（如 100)。因为参数 n=3 是奇数，所以三叶玫瑰曲线的闭合周期为π。 只要将参数 θ从0变化到 π，就能利用玫瑰曲线的参数方程求出平面内的一系列连续的点的坐标（x，y)，由此可构成三叶玫瑰曲线的图形。

 

　　绘制玫瑰曲线的编程思路： 在一个循环结构中让参数 θ从 0 变化到π，再利用玫瑰曲线的参数方程求出点坐标x和y的值，并通过海龟绘图库绘制一系列连续的点，最终绘制出一个完整的玫瑰曲线图。

3.3.编程解题

　　根据上述算法分析中给出的编程思路，编程绘制玫瑰曲线的图形。这个案例需要用到海龟绘图的知识.，请回顾上一节介绍的海龟绘图方法。

　　首先我们来看Python的代码：

'''
程序：绘制玫瑰曲线
作者：苏秦@小海豚科学馆公众号
来源：图书《Python趣味编程：从入门到人工智能》
'''
from turtle import *
from math import *

def draw(a, n, end):
    '''绘制玫瑰曲线'''
    t = 0
    while t <= end:
        x = a * sin(n * t) * cos(t)
        y = a * sin(n * t) * sin(t)
        goto(x, y)
        t = t + 0.01

if __name__ == '__main__':
    '''三叶玫瑰'''
    draw(100, 3, 3.14)
    '''六叶玫瑰'''
    #draw(100, 1.5, 12.56)

　　在上面的代码中可以看出，Python除了要导入海龟绘图库外，还要导入数学库，因为玫瑰曲线函数中涉及三角函数，需要用到 Python 内置的数学库。

　　用于绘制玫瑰曲线的 draw()函数有3个参数，其中参数变量 a 表示叶子的长度，参数变量 n 表示叶子的数量，参数变量 end 表示曲线闭合周期。

　　在函数体中，通过 while 循环结构画出一系列连续的点，循环变量为t，循环控制条件为 t <= end，即在从 0 到 end 的范围内绘制一个闭合的玫瑰曲线。

　　在循环体中，使用玫瑰曲线的参数方程求出点坐标 x 和 y 的值，再利用海龟绘图库提供的 goto（x，y)函数定位画笔就能绘制出相应的图形。 为了绘制出平滑的曲线，循环变量t每次以0.01 的幅度增加。

　　上面代码中的main函数中“三页玫瑰”的代码调用 draw()绘制出一个叶子长度为 100 的三叶玫瑰曲线。由于叶子数3是奇数，所以闭合周期为π ，这里选取 3.14 即可。它绘出的图形如下：

 

　　然而“六叶玫瑰”的参数n=1.5，end=12.56，这又是怎么得来的呢？下面我们来讨论玫瑰线参数的特性。

　　当在整数范围内讨论参数n时，玫瑰曲线的参数特性:若n为奇数，则玫瑰曲线n个叶子数，闭合周期为π，即θ取值为0~ π；若n为偶数，玫瑰曲线2n个叶子数，闭合周期为2π ，即θ取值为 0~2π。

　　当在有理数范围内讨论参数n时，可利用公式  确定玫瑰曲线的叶子数和闭合周期。n为非整数的有理数，L/W为简约分数，参数L控制叶子数，参数W控制闭合周期。玫瑰曲线的参数特性：当参数L和W仅有一个是偶数时，则闭合周期为2Wπ，叶子数为2L；当参数L和W都是奇数时，则闭合周期为Wπ ，叶子数为L。

在下图中展示的是玫瑰曲线 7 代图谱,位于顶端的数字表示参数 L 的值，位于左端的数字表示参数W 的值，通过选择 L 和W 的值，就能确定玫瑰曲线的图形。

 

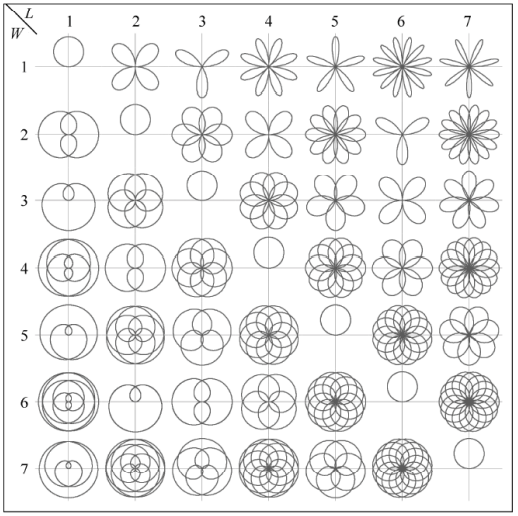
　　所以，当 L=3、W=2 时，则n=1.5，闭合周期为 2Wπ  =12.56。 根据这两个参数就可以绘制出六叶玫瑰曲线图形。如下图：

　　好了，我们已经知道了绘制玫瑰曲线的原理，转换为Julia语言来实现相比也不困难。

　　当然还是要请出Julia的海龟绘图库Luxor，在上一节中已有介绍。不过，笔者在Luxor中没有找到类似Python海龟绘图库turtle中的goto（）函数，所以只能自主实现了自定义函数Goto（）。

　　完整代码如下：

"""
程序：Julia绘制玫瑰曲线
Python原作者：苏秦@小海豚科学馆公众号
来源：图书《Python趣味编程：从入门到人工智能》
"""

using Luxor

#实现海龟画线，从原坐标点到目标坐标点
function Goto(t::Turtle,p::Point)
    oldx, oldy = t.xpos, t.ypos
    t.xpos=p.x
    t.ypos=p.y
    if t.pendown
        gsave()
        sethue(t.pencolor...)
        line(Point(oldx, oldy), Point(t.xpos, t.ypos), :stroke)
        grestore()
    end
end

#绘制玫瑰曲线'''
function draw(t::Turtle,a, n, stop)
    s = 0
    while s <= stop
        x = a * sin(n * s) * cos(s)
        y = a * sin(n * s) * sin(s)
        Goto(t,Point(x,y))
        s = s + 0.01 
    end
end
function main()
    Drawing(300, 300, "mgqx.svg")
    origin()
    turtle=Turtle()
        #三叶玫瑰曲线
        draw(turtle,100, 3, 3.14)
    finish()
end
main()

绘制的三叶玫瑰图如下：

　　可以发现，上图与Python绘制的三叶玫瑰曲线上下颠倒了，当然这关系不大，只能说明Luxor的海龟与Python的turtle移动方向是相反的。

• 扩展阅读

在用海龟绘图库实现绘制玫瑰曲线之后，我们并不打算就此停步。因为原书作者是用参数方方程作为编程的数学模型：

$$\{\begin{array}{c}x=a\ast \text{sin}n\theta \ast \text{cos}\theta \\ y=a\ast \text{sin}n\theta \ast \text{sin}\theta \end{array}$$

而我们打算回归玫瑰曲线的极坐标方程：

ρ=a∗sinθ

　　而且，无论是Python还是Julia都有丰富的科学计算和数据可视化绘图库，相比于海龟绘图库更加高效。因此我们用极坐标方程作为数学模型，并采用其它可视化库来看看如何绘制玫瑰曲线。

　　经过这么些年的发展，Julia的绘图库也日渐丰富，比较常用的有Gadfly, Plots, PyPlot库等，大家可以在下面的网址查看这些库的说明：https://juliapackages.com/c/graphics。

　　本文选用PyPlot.jl库来实现绘制玫瑰曲线。PyPlot库实际上是一个经典的Python绘图库Matplotlib的一个模块，PyPlot.jl提供了一个接口用于调用Matplotlib.PyPlot模块，所以在使用它之前需要先安装matplotlib：

　　方法一，使用pip安装matplotlib

　　pip install matplotlib

　　方法二，使用pip安装光速安装matplotlib如果安装太慢，可替换国内的下载源

　　pip install matplotlib -i https://pypi.tuna.tsinghua.edu.cn/simple

　　然后我们用之前介绍的Julia的库安装方法来安装PyPlot.jl库，或者直接在Julia终端环境输入using PyPlot,然后根据提示操作即可。

所谓玫瑰曲线就是在平面内,围绕某一中心点平均分布整数个正弦花瓣的曲线，在极坐标下可表示为ρ=a*sin(nθ),a为定长,n为整数,来看完整代码：

using PyPlot
function draw()
    theta=0:0.01:2*pi
    #上面返回一个array对象，其元素从0-2*pi，步长0.01
    subplot(111,polar=true) #设置为极坐标模式
    #6瓣花瓣
    plot(theta,sin.(6*theta),linewidth=2.0, linestyle="-")
    #5瓣花瓣
    plot(theta,sin.(5*theta),linewidth=2.0, linestyle="--")
    #4瓣花瓣
    plot(theta,2*sin.(4*theta),linewidth=2)
    rgrids((0.5:0.5:2),angle=45) #网格线
    thetagrids([0,45,90])#角度值
    show()
end
draw()

运行后，会打开一个图形窗口，显示所画的图形：

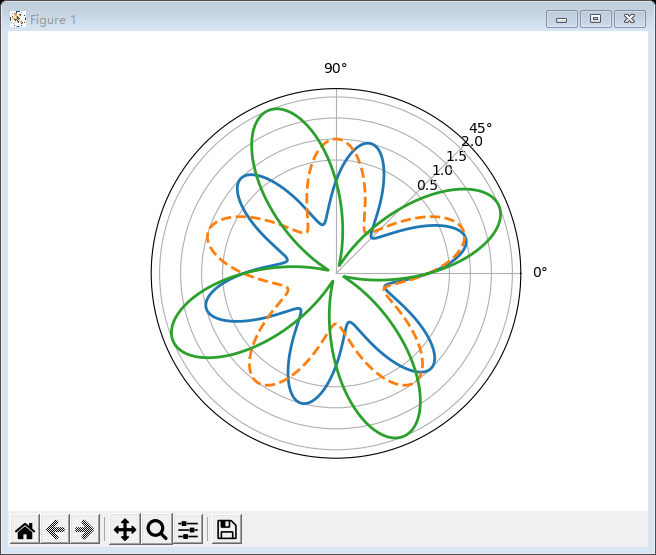
怎么样，是不是很漂亮！