本栏目(Machine learning)包括单参数的线性回归、多参数的线性回归、Octave Tutorial、Logistic Regression、Regularization、神经网络、机器学习系统设计、SVM(Support Vector Machines 支持向量机)、聚类、降维、异常检测、大规模机器学习等章节。内容大多来自Standford公开课machine learning中Andrew老师的讲解和其他书籍的借鉴。
第十二讲. 推荐系统——Recommender Systems
===============================
(一)、Problem Formulation
(二)、基于内容的推荐算法
(三)、协同滤波推荐算法
(四)、算法的矩阵实现
=====================================
(一)、Problem Formulation
什么情况下需要设计一个所谓的推荐系统?
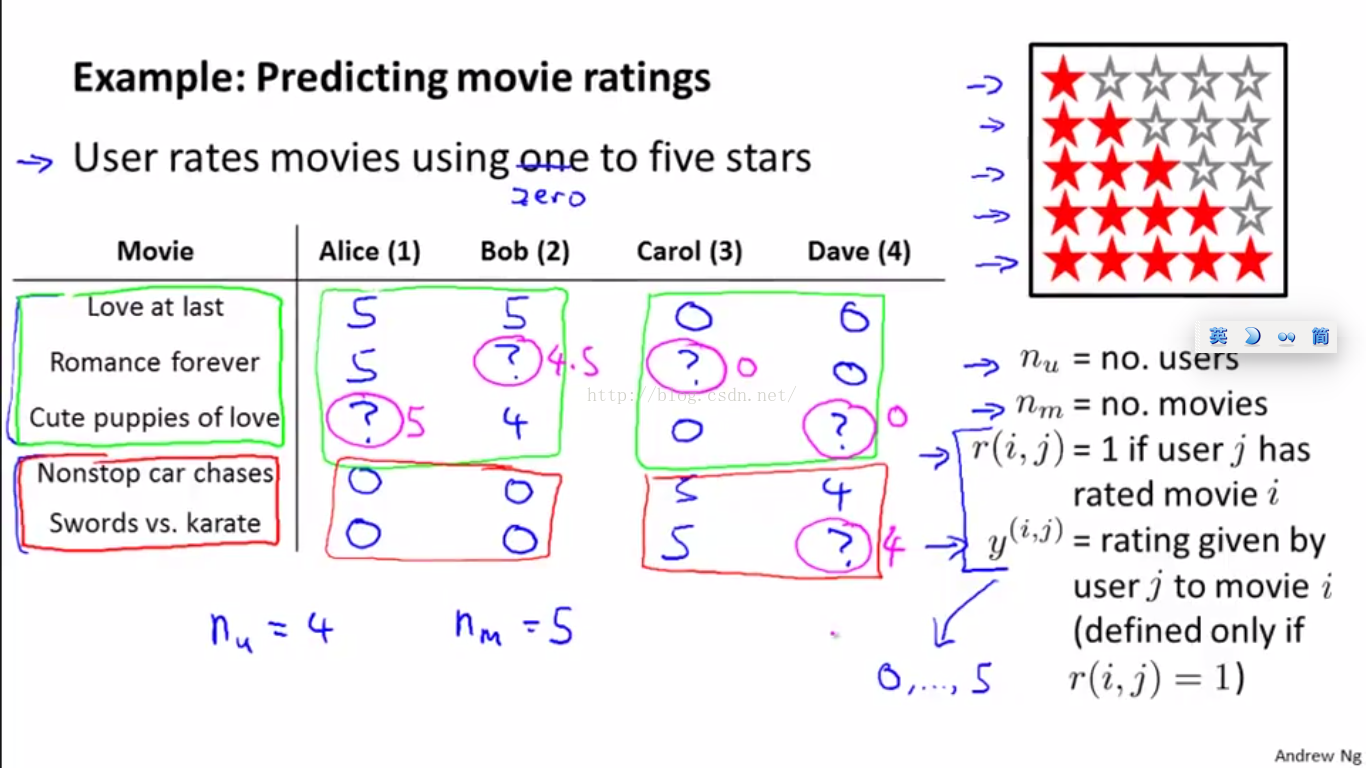
举例说明,如下图,用户给电影打分的例子。
假如我们有4个用户,5部电影。分数等级划分为5个,1~5颗星,分别对应打分1~5,分数越高表明用户越喜欢,问号表示当前用户没有给当前电影打分。
r(i, j)=1 表示用户j已经给电影i打过分了,否则表示未打分;
y(i, j) 表示用户j给电影i打的分数,当然是当r(i, j)=1时才有效。
按照下图的例子,我们来简单说明下推荐系统是用来干嘛的。通过图中表格中的数据我们可以得到以下判断:
1、Alice和Bob给前三部影片打分较高,后两部较低;Carol和Dave则相反
2、前三部影片或许属浪漫爱情片,后三部属动作冒险片。(当然主要是通过影片名称猜测的)
3、根据表格中的数据,我们不难推断,Alice和Bob更喜欢浪漫爱情片,而Carol和Dave则更喜欢动作冒险片
4、由此,我们可以大胆猜测,Alice给第三部影片的打分可能是5,Bob给第二部影片的打分可能是4.5,Carol给第二部影片的打分可能是0,Dave对第三部影片的打分也可能是0,而给第五部影片的打分则接近4.
以上是人根据数据进行的推断,那么我们希望计算机也可以做这件事情,也就是通过分析表格中的数据给用户推荐他可能会喜欢的电影、猜测用户的喜好等等。可以让计算机完成这个任务的系统,就起名叫做推荐系统。
(二)、基于内容的推荐算法
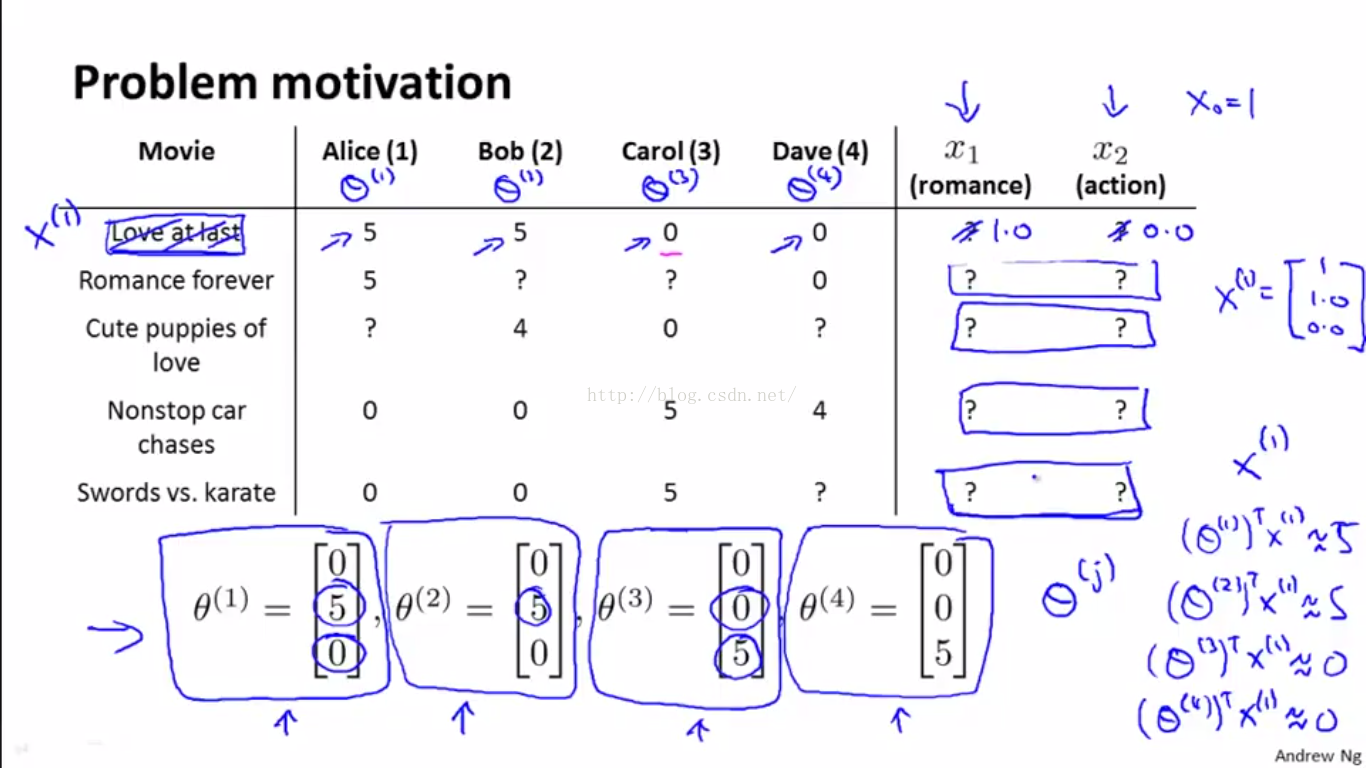
所谓基于内容,是指我们假设已知每部电影的特征描述。比如,第i部电影 的特征有两维,分别描述其浪漫爱情的成份和动作冒险的成份。如果加上偏置项1,令
=1,则如下图所示,描述第一部电影《Love at last》的特征向量应写作
,同理描述第四部电影《Nonstop car chases》的特征为
。已知电影内容的描述向量,我们便可以设计一个基于内容的推荐算法了。
算法的目标是:学习每个用户的喜好,即为每位用户学习一个特征向量,来描述该用户对不同内容电影的喜欢程度,当然用户的特征向量维度是和电影的一致的。正如下图中的 formulation,我们可以用 来描述用户j的喜好,那么自然对应
的第2项应接近为5,而第3项接近为0(此处暂不考虑尺度问题,并忽略第1项偏置项),因为从表格数据中看用户Alice更喜欢浪漫爱情片而非动作冒险片。

有了以上分析以后,我们就可以对上述问题建模了。我们希望 接近用户j对电影i的真实打分 y(i, j) ,就有了下面的目标函数:

当有多个用户时,就是对每个用户分别学习 向量了。可以看到,基于内容的推荐算法的目标函数长得有点像线性回归的目标函数,其实当只考虑一个用户时,我们确实是在尝试学习一个线性回归模型,为每个用户拟合一条“评分-电影特征“的曲线。
目标函数的解法:
一般采用梯度下降法。迭代公式也类似线性回归目标函数的求解,如下:

(三)、协同滤波推荐算法
上一节中的基于内容的推荐算法,我们假设电影的特征描述是已知的,但是往往我们得到这个已知量是比较难的,或者是不准确的。而我们这节要介绍的协同滤波推荐算法,可以自动获取电影的特征描述,而不需人工标注。
一、未知电影的特征描述,但已知用户的喜好特征
下图描述了已知 未知 x 的情况:
这种情况下,我们可以像上一节的基于内容的模型一样,目标函数是一样的,只是求解的变量变了,如下:
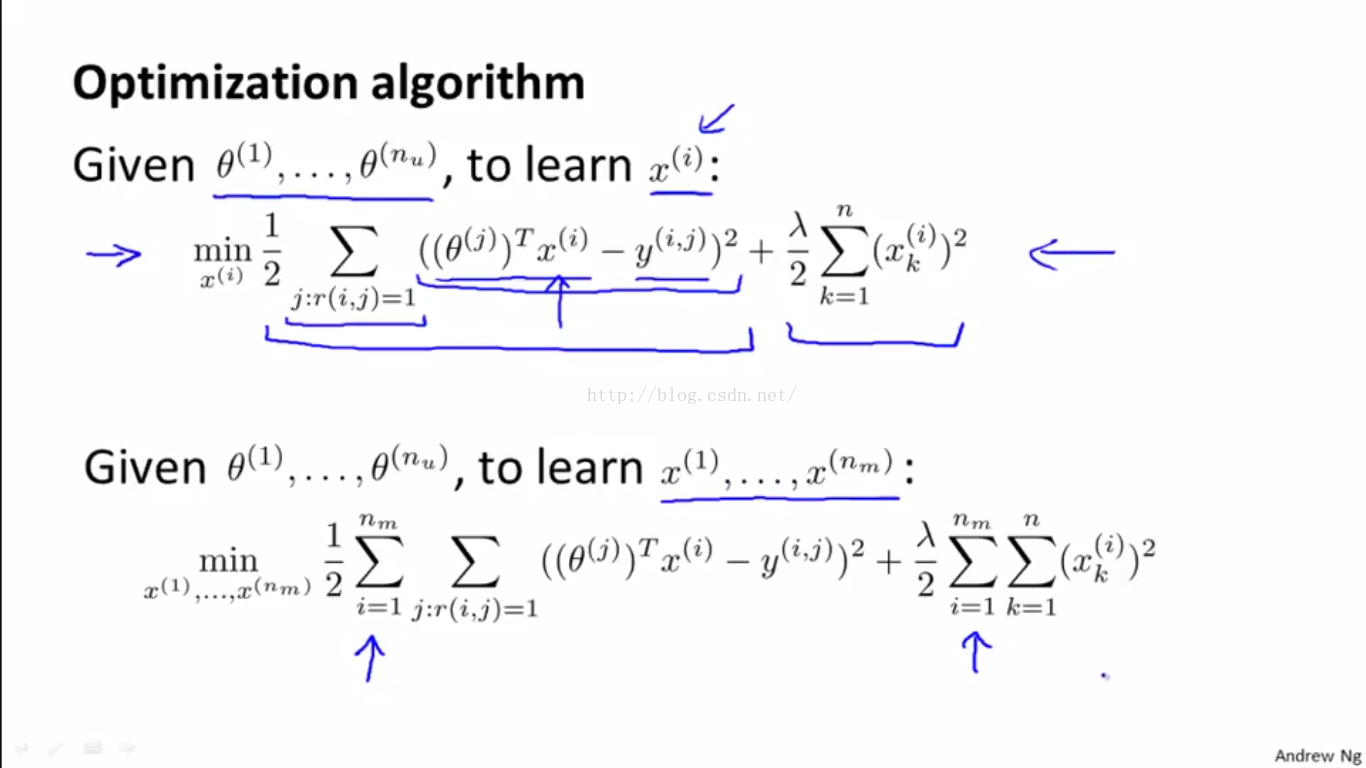
二、当二者都未知时,便采用协同滤波算法
如果电影的特征描述和用户的喜好描述都没有,我们便可采用协同滤波的推荐算法。该算法的思想如下:
既然 x 和 ,已知其中一个都可以估计出另一个,那么当两个都未知时,我们只需给二者中的任意变量赋一个初值,然后求解另一个,然后再更新这个变量,再求解另一个变量,这样循环往复(如下图所示),直到目标函数收敛。

三、协同滤波算法
了解了协同滤波推荐算法的原理以后,我们就可以有简单的算法设计思路了。
1、目标函数

2、算法流程

(四)、算法的矩阵实现
本节简单介绍一下上述算法的矩阵表示方法,知道这个可以帮助我们理解该算法线性代数层面上的矩阵或向量表达,从而在实际应用中快速编程实现算法。
一、算法的矩阵表示
如下图,我们可以把用户的评分,即训练数据的ground truth,放在一个大的Y矩阵里保存下来
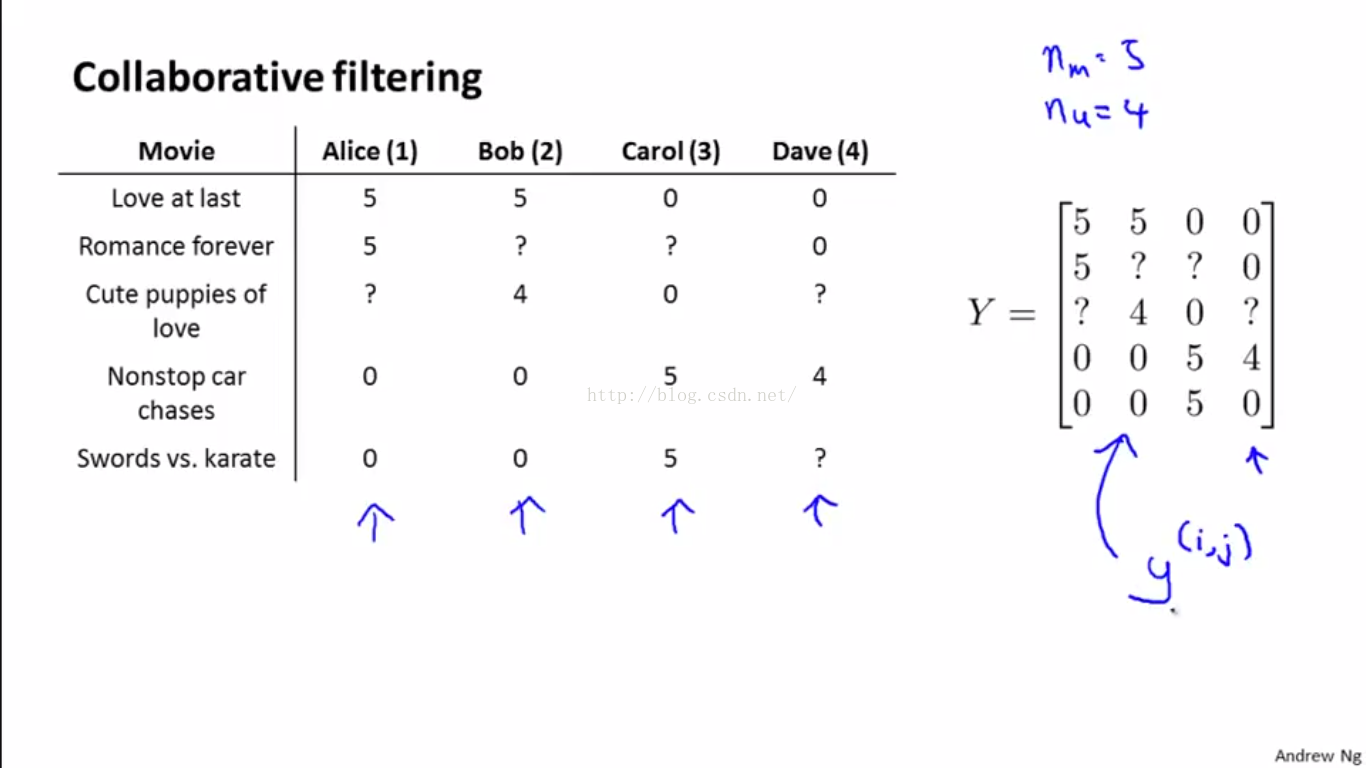
而预测结果用矩阵表示则如下:
将右侧矩阵转化成矩阵乘积的形式,如下:
写成这种矩阵乘积的形式以后,就便于用程序语言实现算法了
二、电影相关性
对模型以及数据矩阵化或者向量化表达以后,我们再探讨计算电影相关性的问题,就方便多了。
思想很简单:
我们上面已经介绍过用向量 x 来描述电影的内容、属性等,那么 x 就可以作为电影的特征向量。两个向量差的模值、范数等,都可以用来描述两部电影的相似度、相关性。so easy~
三、均值向量规范化
这是一个实现算法的小的技术细节问题,下面我们来简单阐述一下。
1、Problem Motivation
先来说说提出“均值向量规范化”这个技术细节的动机。如下图所示:
当第5个用户 Eve 对所有电影都没有评价时,r(i, 5) 全部是0。所以当j=5时目标函数的第一项不存在,即为0。优化问题就变成了使上图公式的最后一项最小,得到的解便是 的所有项均为0,则与任意 x 向量相乘的结果也均为0。这不是我们想要的,这样的学习和预测结果都是毫无意义的。
2、用均值向量规范化来解决上述问题
具体如下图:
(1)计算均值向量:计算每部电影的平均得分(没打分的问号处不计算在内),得到五部电影的平均得分向量。
(2)均值向量规范化:然后用分数矩阵Y减去该向量,得到上图右侧的新矩阵Y。
(3)训练:将新的Y矩阵作为训练数据,学习 x 和 theta。
(4)预测:与之前不同的是,这时预测需要重新加上均值向量:
例如,学习得到的用户 Eve 的特征向量,元素仍然全部为0,但是因为要加上均值向量计算评分,所以预测结果自然不会是0了。
分析说明:这样做的实际结果是,预测出来的用户Eve对电影的评分,就等于其他用户对电影的平均打分。可想而知,这是合乎常理的,因为当你什么都不知道的时候,假设数据是呈均匀分布的,或许是个不错的先验。



