异常检测:
判断测试集是否异常。如下例中对飞机引擎的判断:

我们建立评估模型概率模型p(x)来判断,如果p(x)<ε异常,反之正常

用处举例:购物网站用户异常检测,计算机集群异常检测
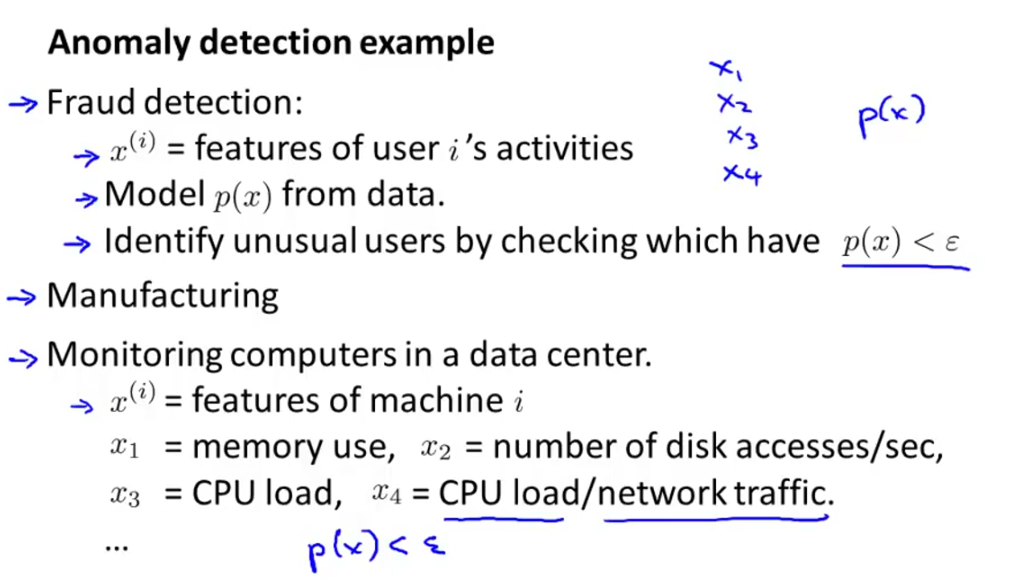
算法实现:
建立评估模型:

1.选择相应的变量。
2.变量拟合高斯分布。
3.计算概率。

两个参数时的概率模型图:

模型实例:

数据的分配:(推荐使用前一种方式)

模型建立:

模型评估:

可以尝试不同的阈值来调整模型。
监督学习和异常检测的区别

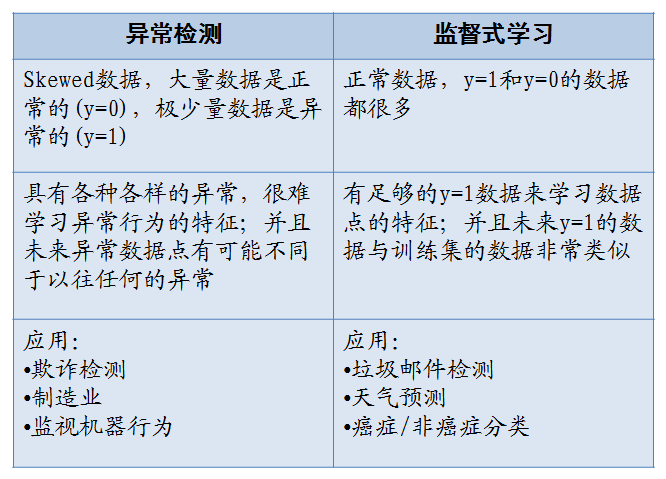
总结:误差检测模型(正例数量大,负例数量很小)
(五)、如何选取或设计feature
下面我们说说异常检测问题中的feature应如何选取或设计。
这部分将介绍两个方面:一是数据变换,二是增加更具辨别力的feature
一、数据变换
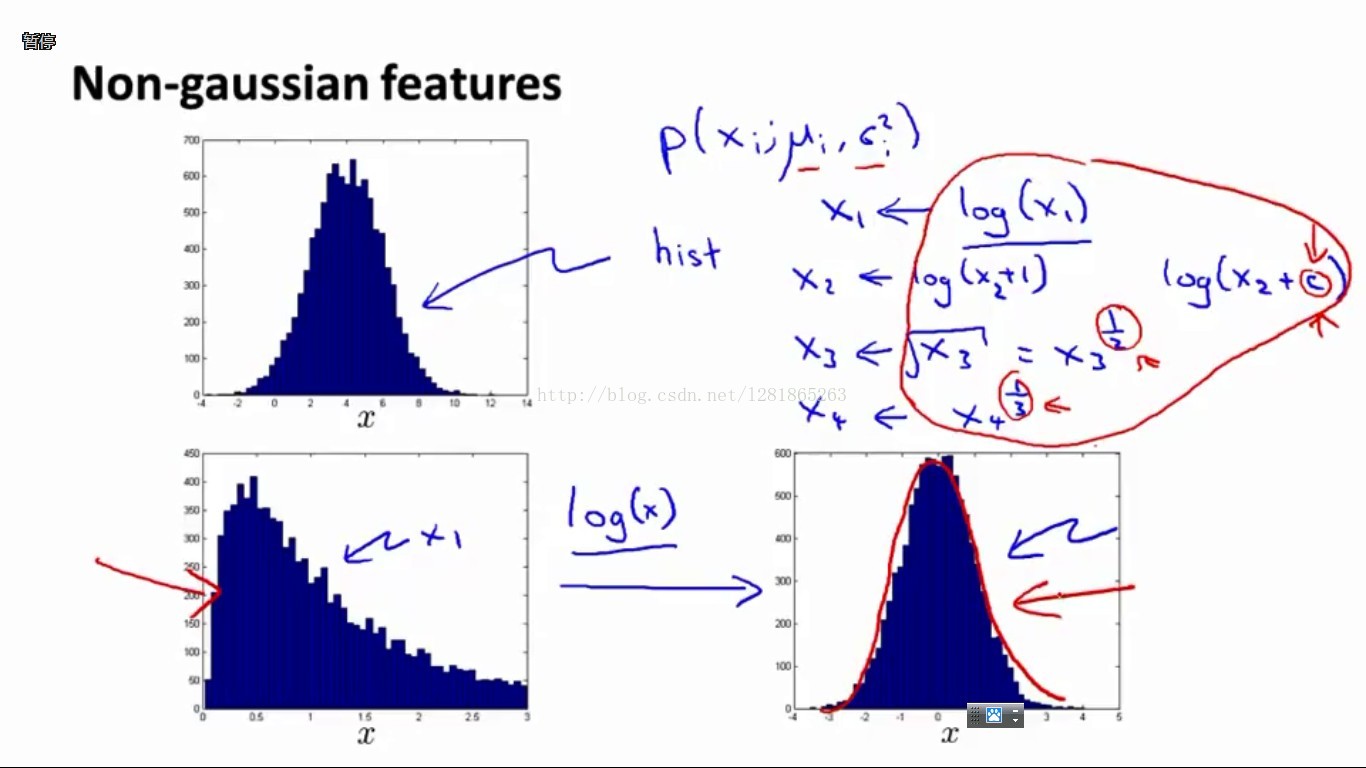
我们知道,上述异常检测系统是建立在每一维数据都服从高斯分布的假设基础上的。那么如果原始数据并不服从高斯分布呢?办法就是,先对原始数据进行某种变换,其实也相当于是设计新的feature。举例说明如下图:
左上图:统计数据x的直方图,发现基本符合高斯分布
左下图:发现数据的直方图并不符合高斯分布
右下图:对x进行log(x)变换以后,统计直方图基本符合高斯分布了
类似log(x)的变换有很多,如右上显示的几种函数都可以在实验时尝试。
下面举个实验中的例子,具体阐述一下如何做数据变换。如接下来的几幅图所示,代码是Octave的:
初始数据是这个样子的:
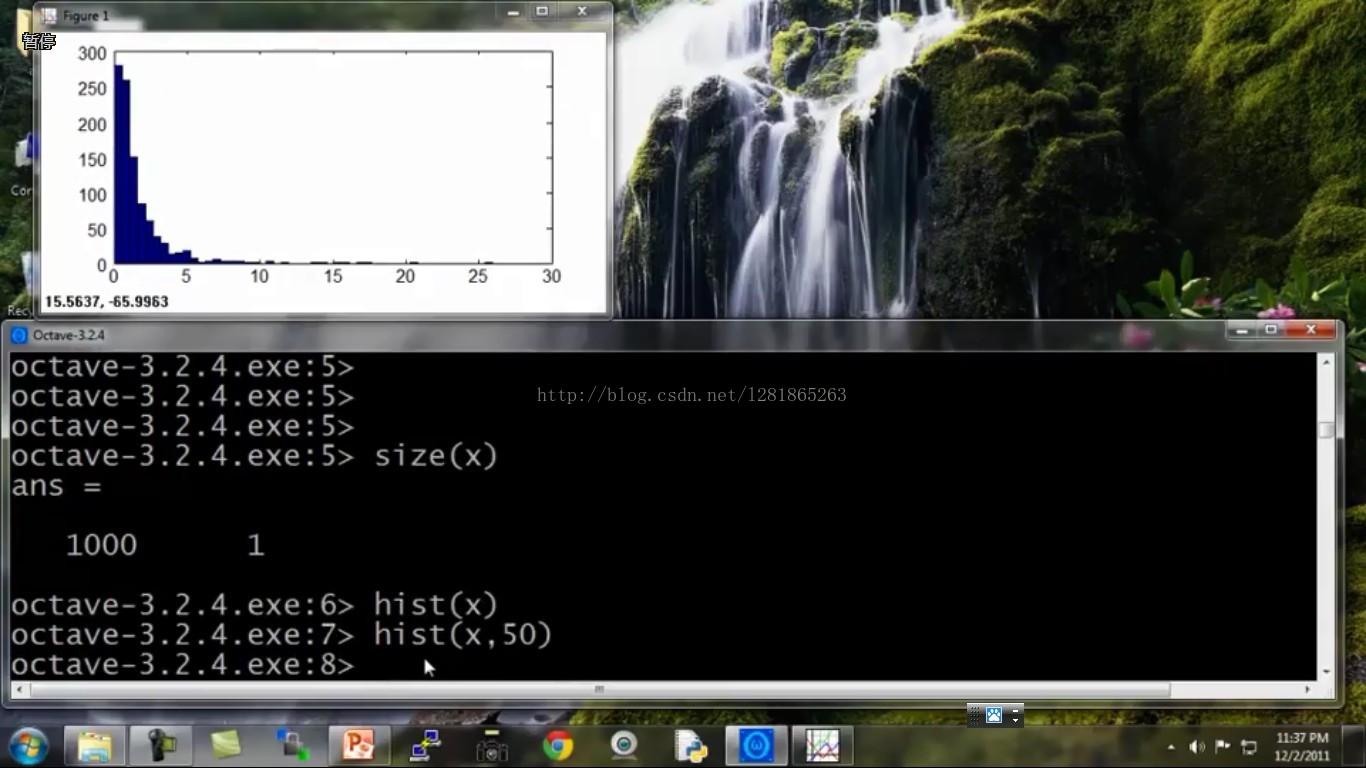
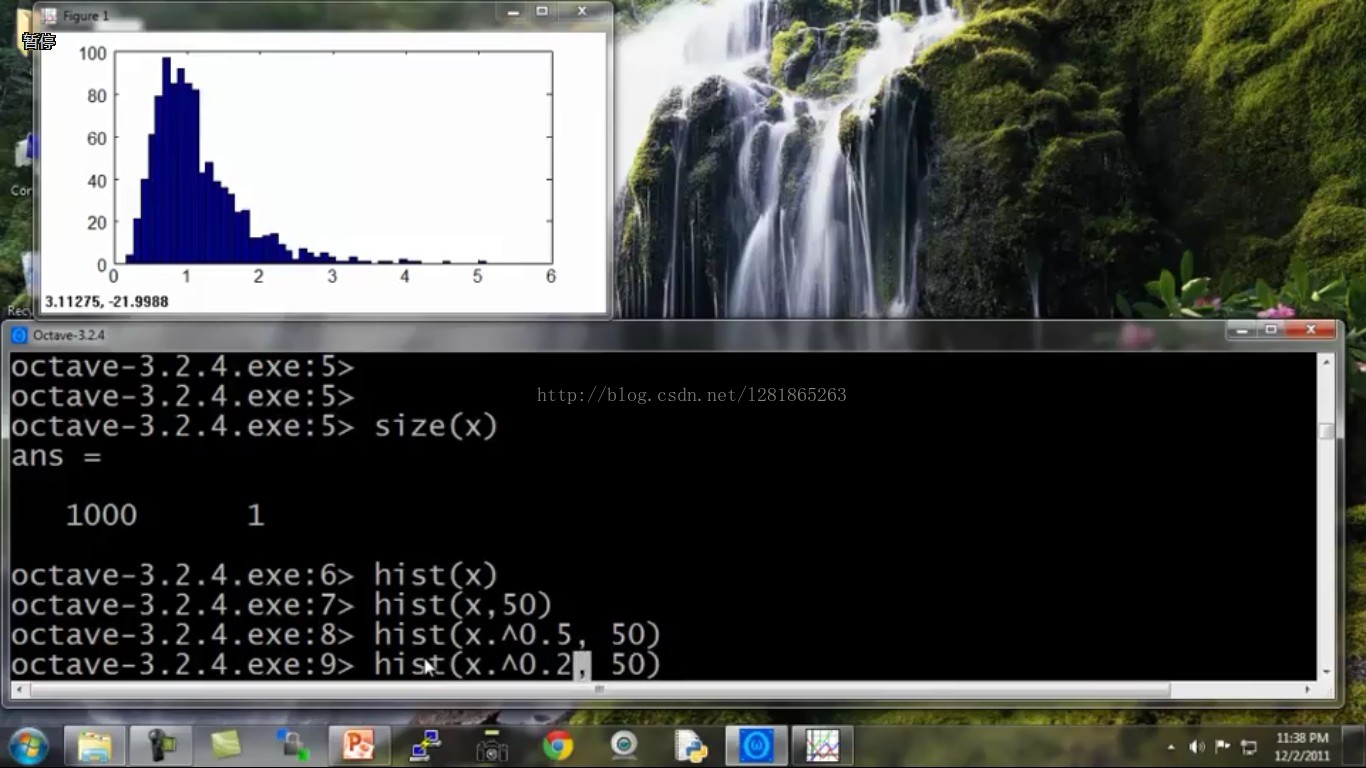
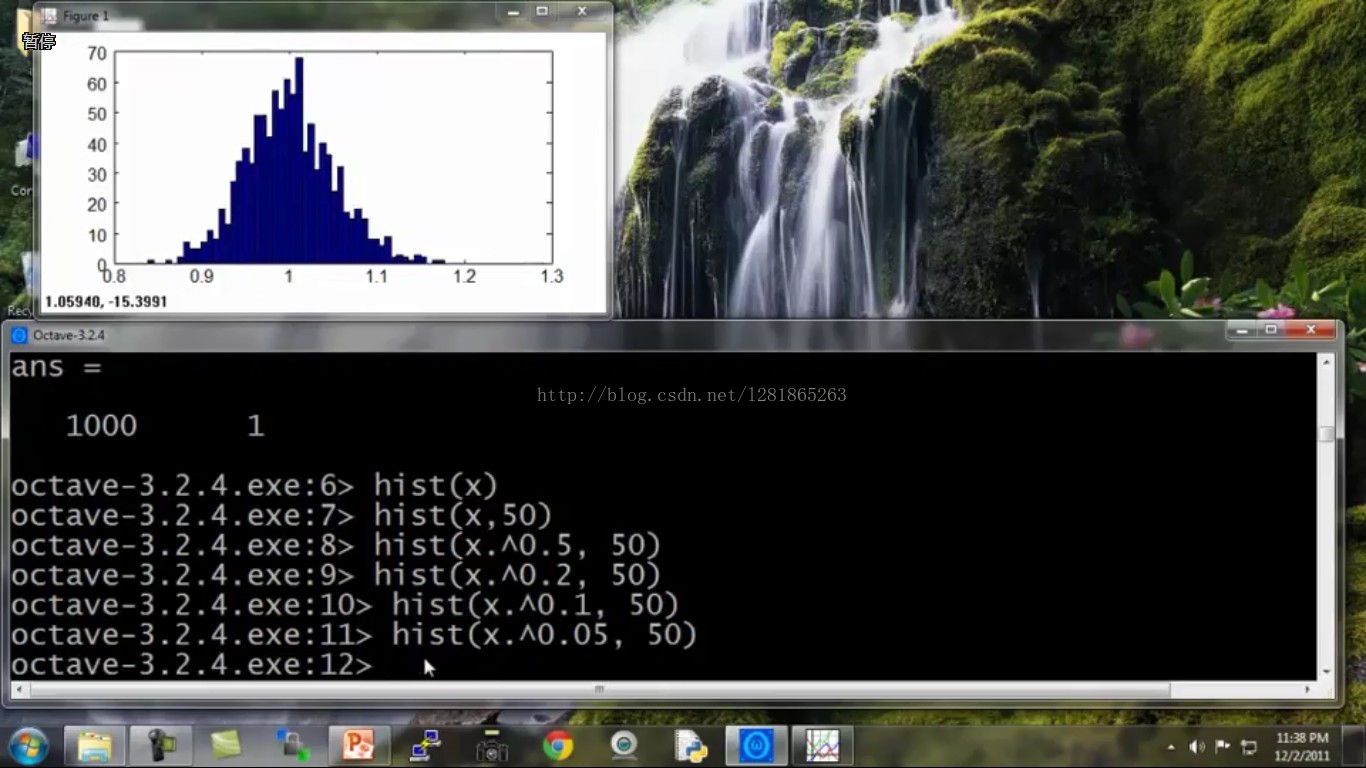
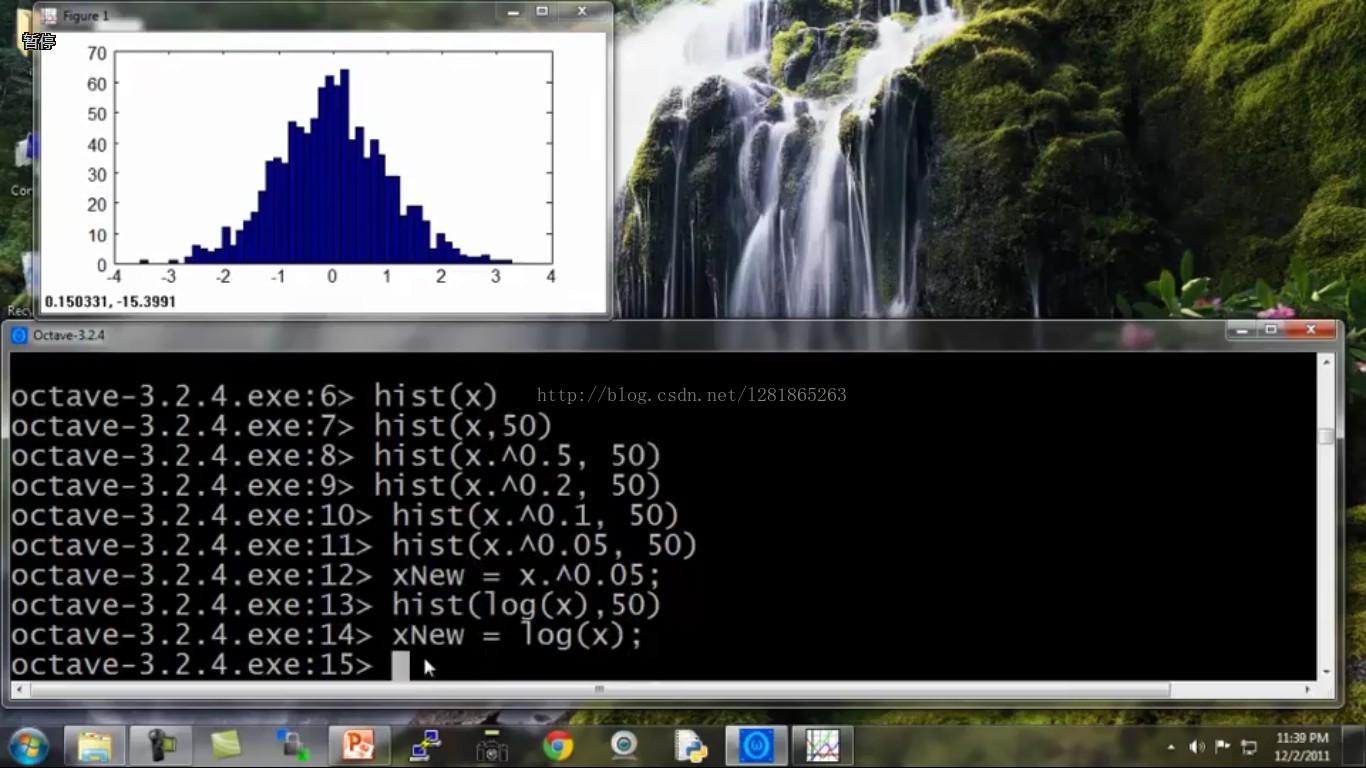
将变换后的符合高斯分布的数据赋值给新的xNew,拿xNew去估计高斯分布的两个参数即可。大功告成!
二、增加更具辨别力的feature
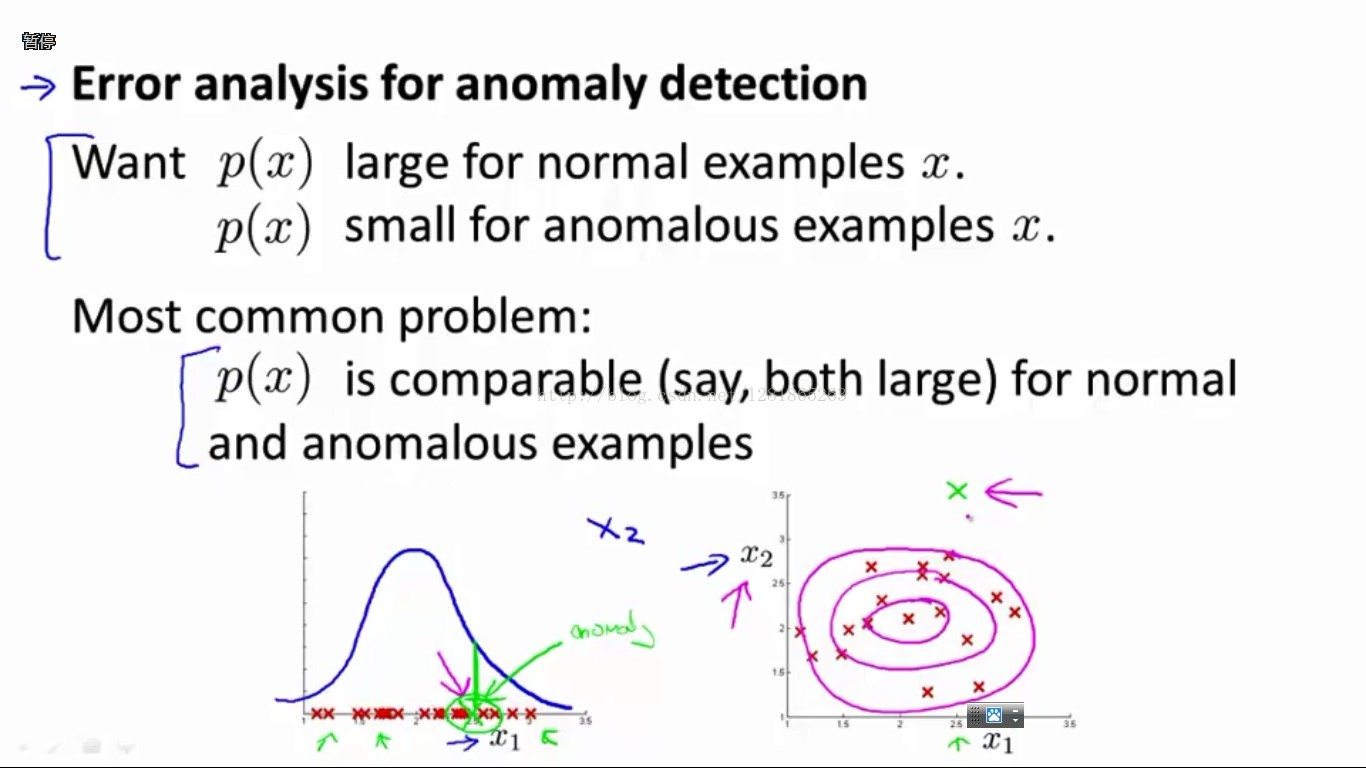
此外,由于我们是靠概率阈值来区分正常和异常样本的,我们当然是希望异常样本的概率值小且正常样本的概率值大。这时容易碰到的问题便是,如果一个测试样本的预测概率值不大不小恰好在阈值附近的话,预测结果出错的可能性就比较大了。如下图所示:
在绿色X样本的位置,预测概率值对于正常和异常样本来说都挺大的,很难给出一个正确的判断。

这时,如果我们有另外一个维度的特征,在绿色X的位置附近对于正常和异常样本更有区分度,那么我们可能就可以对绿色X做出正确的判断了。如下图所示,我们增加x2特征以后,发现绿色X样本在x2这个特征维度上的概率p(x2)很小,与p(x1)的乘积自然也较小。从而,当特征x1无法区分时,特征x2帮助模型成功辨别了该样本。
综上,选取特征时注意两点:
1、当特征数据不符合高斯分布时,通过统计数据的直方图分布,尝试用多种函数变换数据,使直方图分布特性符合高斯模型。
2、当前特征区分度不够时,可设计增加更有区分度的特征,以帮助模型更具辨别力。
(七)、多元高斯分布及其在异常检测问题上的应用
一、Motivation
为什么又有了多元高斯分布的概念呢?下面为了引入motivation,我们举个用多元高斯分布比用上述高斯分布模型更靠谱的栗子
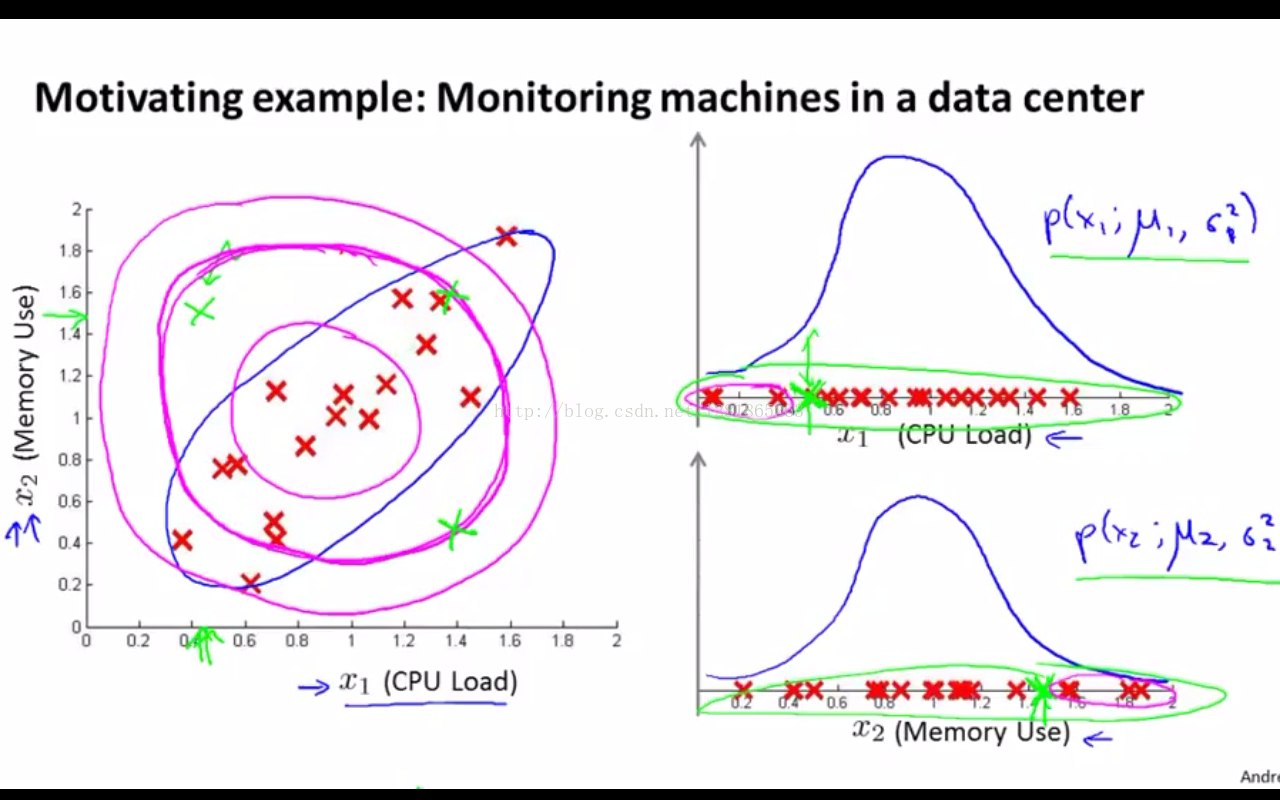
如下图所示,当x1和x2存在左图中的线性关系时(这里可以先不用在意二者的线性关系,后续会详细讲解),绿色X样本的p(x1)和p(x2)都在阈值范围内,也就是都没有小到判为异常样本的程度(如右图),那么它们的乘积自然很有可能也不满足异常样本的判定条件。具体地,如左图,紫色的圆圈越往外,属于正常样本的概率就越小,圆心点的概率最大。这时我们看到绿色X测试样本和几个红色X训练样本距离圆心的距离是相近的,也就是拥有相似的概率值,那么绿色点就会被判为和红色一样是正常样本了。
二、多元高斯模型公式
与上面介绍的假设每一维数据都是相互独立的高斯分布模型不同的是,多元高斯分布整体考虑所有维度的数据。
同样有两个参数,均值和协方差矩阵,公式如下图所示,其中 |Sigma| 表示的是协方差矩阵Sigma的行列式。

注意,我们上面所说的x1和x2存在的线性关系,实际上就蕴含在协方差矩阵中,所以也就是说多元高斯分布与相互独立的一元高斯分布之间的差异就在于,前者考虑了不同数据分布之间的关系,而后者则认为它们是无关的、独立的。
接下来举例说明多元高斯分布模型与数据关系之间的联系:
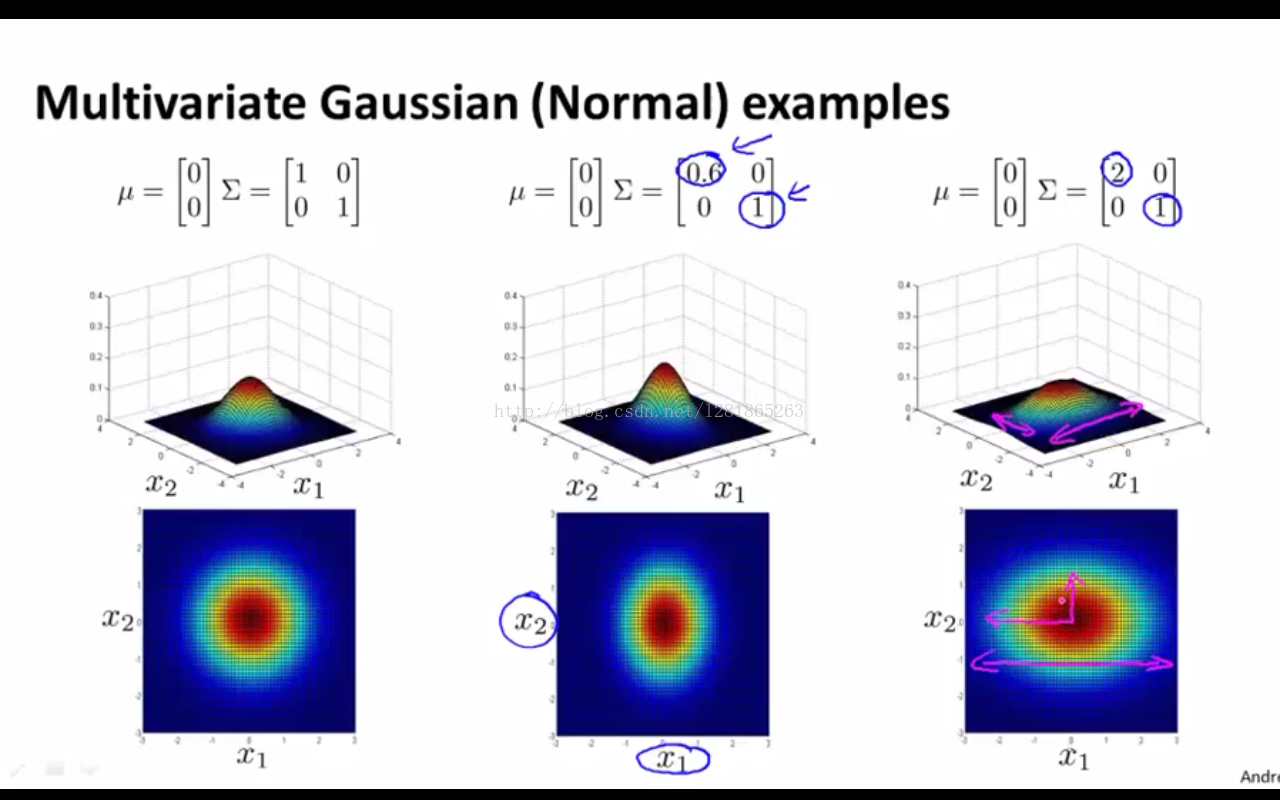
(1)如下图,当协方差矩阵的对角线元素相等时,三维空间中的模型曲面在两个维度上展开范围也是相等的

(2)如下图,当对角线元素不等时,曲面在两个维度上的展开范围大小有了区分。如右一的图,概率值沿x2方向比沿x1方向下降得快。
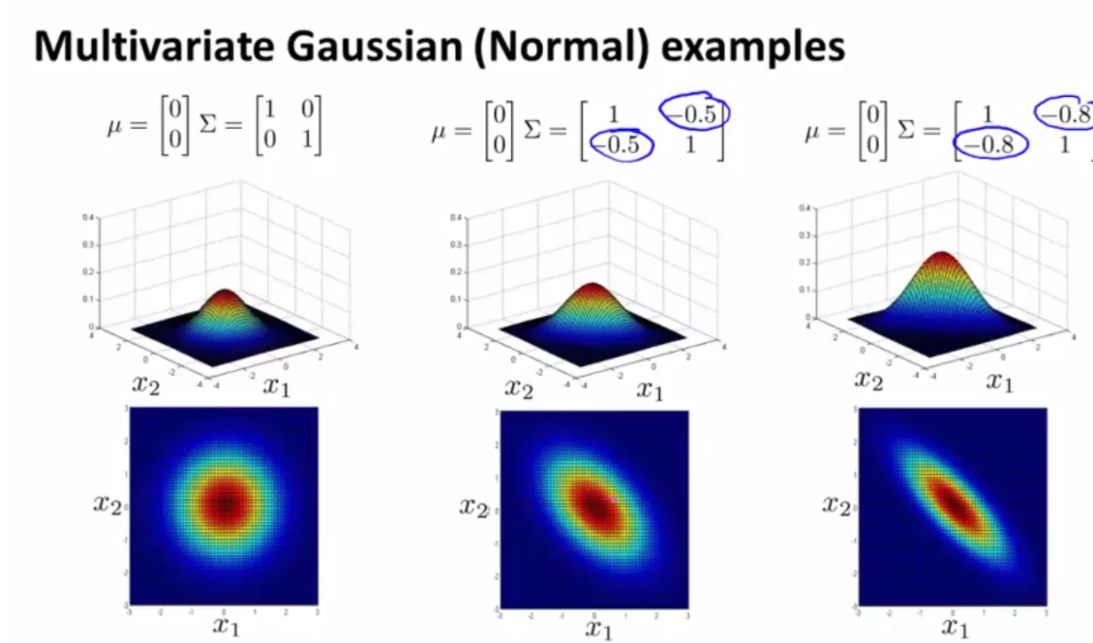
(3)下面几张图的变换也很重要,只是这里不做详细解释了。大家可通过观察协方差矩阵和均值向量的值,结合看相应的图形,来体会多元高斯模型与数据关系之间的联系。


三、用多元高斯模型建模的异常检测算法
算法如下图所示:

观察上图的右图可见,当用多元高斯模型时,如果两个维度的数据存在某种线性关系,这种关系会很容易被捕捉到,并正确指导测试样本的判别。
四、多元高斯模型与多个独立的一元高斯模型之间的联系
不难发现,其实,后者是前者的特殊形式,其关系如下:
当且仅当协方差矩阵是一个对角阵时,且对角元素等于各个维度的方差,则此时的多元高斯模型就等价于多个独立的一元高斯模型。如下图:

也就是说,这种特殊情况下,各个维度的feature之间相互独立,不存在任何线性或非线性关系,从而三维曲面只在不同维度上有不同的展开宽度,而不会像上面的几个例子那样产生45°的倾斜。
知道了两者的联系以后,我们就要想了,那什么时候用多元高斯模型什么时候假设相互独立的一元高斯模型呢?总结二者的区别如下(前者指多元高斯模型,后者指一元高斯模型):
1、特征选择:
对于同样的一组已知数据,假设{x1,x2},x1和x2都不能很好地区分的话,如果选用后者的模型,正如我们在特征选取一节中介绍的那样,可能需要我们人工设计一个更具辨别力的feature(比如x1/x2);但如果选用前者模型的话,多元高斯模型会自动学习x1和x2的关系,就无需人工设计feature了
2、计算效率:
后者的计算效率更快一些,因为它不涉及到协方差矩阵求逆等一些复杂的矩阵运算。所以当样本维度n很大时,一般n=100,000或10,000时认为很大了,更多采用后者的模型。否则协方差矩阵将是n*n大小的,求逆运算会很慢很慢。
3、关于样本数量m和样本维度n:
综上,当m比较小时,更适合用后者模型,因为少量的样本不容易学到数据间的复杂关系;当m>>n(比如m=10n)且协方差矩阵可逆时,就采用前者多元高斯分布模型。



