如果我们对我们的预测中的错误进行了一些解决:
1.更多的训练样本
2.减少变量
3.尝试额外的参数
4.在多项式的参数
5.增加或减少λ
我们可以评估我们的新假设
假设可能有一个低误差的训练例子但仍然是不准确的(因为过度拟合)。因此,为了评估一个假设,给定训练样本的数据集,我们可以将数据分成两组:一组训练集和一组测试集。通常,训练集由70%的数据组成,测试集是剩下的30%。
使用这两套新程序然后:
1.通过训练样本得到θ,使Jtrain(θ)最小
2.计算测试组的错误率
测试组的错误率
1.对于线性回归:![]()
2.对于分类回归(又名0/1分类错误):
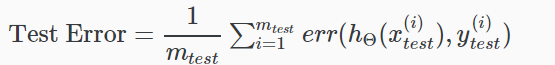
这给了我们一个基于错误分类的二进制0或1错误结果。为测试集的平均测试误差:
![]()
这给我们的测试数据被错误分类的比例。
模型的选择和培训/验证/测试集
就因为一个学习算法很好适应了训练集不意味这这是一个好的算法。这可能使过拟合
因此你在预测集上的结果会很糟糕。您在训练参数的数据集上的错误将低于任何其他数据集上的错误。
考虑到许多具有不同多项式度的模型,我们可以用一种系统的方法来识别“最佳”函数。为了选择你假设的模型,你可以测试每一个多项式的程度,并查看错误结果。
将数据集分解为三组的一种方法是:
1.训练集:60%
2.交叉验证集:20%
3.测试集:20%
现在我们可以使用下面的方法计算三个不同集合的三个独立的错误值:
1.使用训练集最优化得到θ。
2.用交叉验证集求最小误差的多项式度d。
3.用测试集计算误差
这样,多项式d的程度没有被训练使用测试集。



