Note: [At 6:15 "h(x) = -900 - 0.1x" should be "h(x) = 900 - 0.1x"]
当具体应用于线性回归的情况下,可以推导出一种新的梯度下降方程。我们可以用我们实际的成本函数和我们实际的假设函数来代替,并将公式修改为:
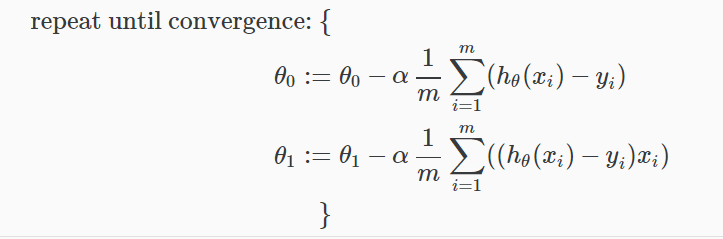
其中M是训练集的规模,θ0常数,将与θ1和xi同时变化的,yi是给定的训练集值(数据)。
注意,我们一句把θj分成独立的θ0和θ1,θ1我们乘xi最后求导
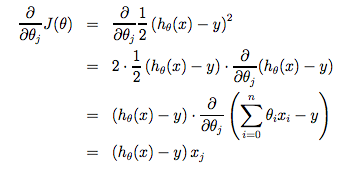
这一切的关键是,如果我们从猜测我们的假设开始,然后反复应用这些梯度下降方程,我们的假设将变得越来越精确。
因此,这只是原始成本函数J的梯度下降。这个方法是在每个步骤的每个训练集中的每一个例子,被称为批量梯度下降。需要注意的是,在梯度下降易总的局部极小值,优化问题,我们在这里提出的线性回归只有一个全球性的,并没有其他的地方,因此总是收敛的最优解;梯度下降(假设学习率α不太大)的全球最低。实际上,j是凸二次函数。这里是一个梯度下降的例子,它是为了最小化二次函数而运行的。
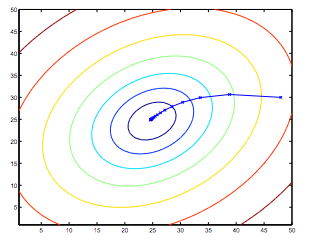
上面所示的椭圆是二次函数的轮廓。也表明是通过梯度下降的轨迹,它被初始化为(48,30)。X在图(连接的直线)的标志,θ梯度穿过它收敛到最小的连续值



