所以我们有了我们的假设函数,我们有一种方法来测量它与数据的吻合程度。现在我们需要估计假设函数中的参数。这就是梯度下降的来源。
想象我们图基于其领域θ0和θ1我们假设函数(实际上我们是图形的成本函数作为参数估计的函数)。我们不是绘制x和y本身,而是我们假设函数的参数范围和选择一组特定参数所产生的代价
我们把θ0在X轴和Y轴θ1,与成本函数在垂直的Z轴。我们的图上的点将是使用我们的假设和特定θ参数的代价函数的结果。下图描述了这样的设置。
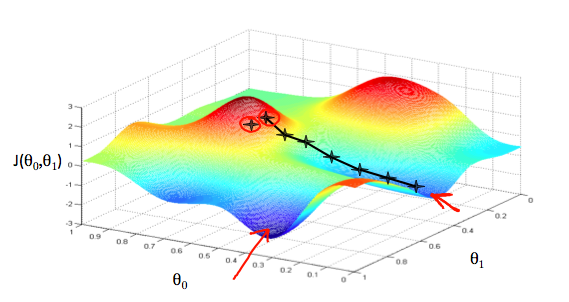
当我们的成本函数位于图的最底部,即当它的值是最小值时,我们就知道我们已经成功了。红色箭头显示图中的最小点。
我们这样做的方法是取我们的成本函数的导数(函数的切线)。切线的斜率是这个点上的导数,它将给我们一个方向。我们把成本函数降到最陡下降的方向。每一步的大小由参数α决定,称为学习率。
例如,上图中每个“星”之间的距离代表由我们的参数α决定的步骤。较小的α会导致较小的步长和较大的α结果。这一步是采取的方向是由J的偏导数确定(θ0,θ1)。取决于图表上的起点,可能会出现不同的点。上面的图片给我们展示了两个不同的起点,终点在两个不同的地
梯度下降算法是:
重复直至收敛:
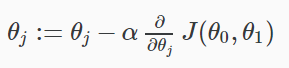
哪里
J = 0,1代表特征指数。
在每一次迭代,同时应更新参数θθ1,2,…,nθ更新特定的参数来计算一个j(th)迭代之前,将产生一个错误的执行




