Let's assume that
- v(n) is the largest prime number, that does not exceed n;
- u(n) is the smallest prime number strictly greater than n.
Find 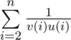 .
.
Input
The first line contains integer t (1 ≤ t ≤ 500) — the number of testscases.
Each of the following t lines of the input contains integer n (2 ≤ n ≤ 109).
Output
Print t lines: the i-th of them must contain the answer to the i-th test as an irreducible fraction "p/q", where p, q are integers, q > 0.
Examples
Input
2
2
3
Output
1/6
7/30
写写1/v(i)u(i)的前几项就能发现规律
i 2 3 4 5
v 2 3 3 5
u 3 5 5 7
如果用个f(i)表示1/v(i)u(i),那么对于一个质数x,有f(2)+f(3)+...+f(x-1)=1/2-1/x
然后在对于一个夹在两质数a,b之间的x,显然从a到x的f值都是a/b,所以就是找到n前后最近的质数,把两分式通分一下就好了
这里我是直接n往前往后Miller-Robin找第一个质数,不过sqrt(n)的暴力应该也能卡过去?

1 #include<cstdio> 2 #include<iostream> 3 #include<cstring> 4 #include<cstdlib> 5 #include<algorithm> 6 #include<cmath> 7 #include<queue> 8 #include<deque> 9 #include<set> 10 #include<map> 11 #include<ctime> 12 #define LL long long 13 #define inf 0x7ffffff 14 #define pa pair<int,int> 15 #define mkp(a,b) make_pair(a,b) 16 #define pi 3.1415926535897932384626433832795028841971 17 using namespace std; 18 inline LL read() 19 { 20 LL x=0,f=1;char ch=getchar(); 21 while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} 22 while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} 23 return x*f; 24 } 25 LL mul(LL x,LL n,LL MOD) 26 { 27 LL res=x*n-(LL)((long double) x*n/MOD+0.5)*MOD; 28 while (res<0)res+=MOD; 29 while (res>=MOD)res-=MOD; 30 return res; 31 } 32 LL qpow(LL x,LL n,LL MOD) 33 { 34 x=(x%MOD+MOD)%MOD; 35 LL p=x,con=1; 36 while (n) 37 { 38 if (n&1)con=mul(con,p,MOD); 39 p=mul(p,p,MOD); 40 n>>=1; 41 } 42 return con; 43 } 44 bool witness(LL a,LL b) 45 { 46 if (a==b)return true; 47 LL s=b-1; 48 int t=0; 49 while (!(s&1))s>>=1,t++; 50 LL x=qpow(a,s,b); 51 if (x==1)return 1; 52 while (t--) 53 { 54 if (x==b-1)return true; 55 x=mul(x,x,b); 56 if (x==1)return false; 57 } 58 return false; 59 } 60 bool isprime(LL x) 61 { 62 if (x==0||x==1)return false; 63 static int p[]={2,3,5,7,11,13,17,19,23,29,31}; 64 for (int i=0;i<=10;i++) 65 if (!witness(p[i],x))return false; 66 return true; 67 } 68 inline LL gcd(LL a,LL b) 69 { 70 if (a<b)swap(a,b); 71 return b==0?a:gcd(b,a%b); 72 } 73 int main() 74 { 75 int T=read(); 76 while (T--) 77 { 78 LL x=read(),y,z,t,ans1,ans2; 79 for (y=x;y>=2;y--)if (isprime(y))break; 80 for (z=x+1;z<=1e9+7;z++)if (isprime(z))break; 81 //ans=1/2-1/y+(x-y+1)*y/z 82 ans1=y*z-2*z+2*x-2*y+2;ans2=2*y*z; 83 t=gcd(ans1,ans2);ans1/=t;ans2/=t; 84 printf("%lld/%lld\n",ans1,ans2); 85 } 86 }
——by zhber,转载请注明来源


 浙公网安备 33010602011771号
浙公网安备 33010602011771号