DZY loves Physics, and he enjoys calculating density.
Almost everything has density, even a graph. We define the density of a non-directed graph (nodes and edges of the graph have some values) as follows:
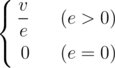
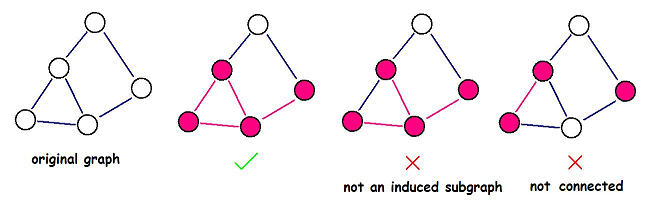
Once DZY got a graph G, now he wants to find a connected induced subgraph G' of the graph, such that the density of G' is as large as possible.
An induced subgraph G'(V', E') of a graph G(V, E) is a graph that satisfies:
-
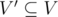 ;
; -
edge
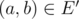 if
and only if
if
and only if  ,
and edge
,
and edge  ;
; - the value of an edge in G' is the same as the value of the corresponding edge in G, so as the value of a node.
Help DZY to find the induced subgraph with maximum density. Note that the induced subgraph you choose must be connected.
The first line contains two space-separated integers n (1 ≤ n ≤ 500), 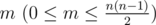 .
Integer n represents the number of nodes of the graph G, m represents
the number of edges.
.
Integer n represents the number of nodes of the graph G, m represents
the number of edges.
The second line contains n space-separated integers xi (1 ≤ xi ≤ 106), where xi represents the value of the i-th node. Consider the graph nodes are numbered from 1 to n.
Each of the next m lines contains three space-separated integers ai, bi, ci (1 ≤ ai < bi ≤ n; 1 ≤ ci ≤ 103), denoting an edge between node ai and bi with value ci. The graph won't contain multiple edges.
Output a real number denoting the answer, with an absolute or relative error of at most 10 - 9.
1 0 1
0.000000000000000
2 1 1 2 1 2 1
3.000000000000000
5 6 13 56 73 98 17 1 2 56 1 3 29 1 4 42 2 3 95 2 4 88 3 4 63
2.965517241379311
In the first sample, you can only choose an empty subgraph, or the subgraph containing only node 1.
In the second sample, choosing the whole graph is optimal.
lwh大神说,这不是01分数规划吗,二分+网络流!
我吓坏了
结果事实证明ccr代码竟然真A了
贪心证明略(废话我当然不知道怎么证)
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
using namespace std;
int x[1000001];
int main()
{
int n, m;
cin >> n >> m;
double ans = 0;
int p, q, c;
for (int i = 1; i<= n; i++)
cin >> x[i];
for (int i = 0; i< m; i++)
{
cin >> p >> q >> c;
ans = max(ans, (double) (x[p] + x[q]) / c);
}
printf("%.10f", ans);
}


