20172311《程序设计与数据结构》第六周学习总结
教材学习内容总结
第十章 树
- 树是一种非线性结构,其中的元素被组织成一个层次结构
- 含有m个元素的平衡n元树具有的高度为lognm
- 树的数组实现之计算策略:
如果我们存储的树不是完全的或者只是相对完全的,则该数组会为不包含数据的树位置分配空间
- 树的数组实现之模拟链接策略:
这种方式使得元素能够连续存储在数组中,因此不会浪费空间,但是该方式增加了删除树中元素的成本。
- 树的遍历
1.先序遍历
即根节点在左右子树之前遍历:
先访问根节点
再先序遍历左子树
再先序遍历右子树
退出
2.中序遍历
先中序遍历左子树
再访问根节点
再中序遍历右子树
退出
3.后序遍历
即根节点在左右子树之后遍历:
先后序遍历左子树
再后序遍历右子树
最后访问根节点
退出
4.层序遍历
即从根节点开始,访问每一层的所有结点,一次一层

以上图为例,三种遍历结果:
先序遍历:
1 2 4 5 7 3 6
中序遍历:
4 2 7 5 1 3 6
后序遍历:
4 7 5 2 6 3 1
层序遍历:
1 2 3 4 5 6 7
-
二叉树的ADT

-
二叉树
二叉树是有限个节点的集合,这个集合可以是空集,也可以是一个根节点和至多两个子二叉树组成的集合,其中一颗树叫做根的左子树,另一棵叫做根的右子树。简单地说,二叉树是每个节点至多有两个子树的树
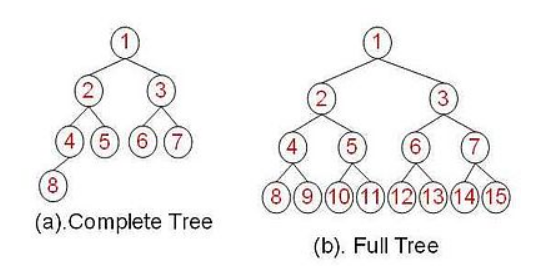
- 完全二叉树
完全二叉树是一种特殊的二叉树,满足以下要求:
1.所有叶子节点都出现在 k 或者 k-1 层,而且从 1 到 k-1 层必须达到最大节点数;
2.第 k 层可是不是慢的,但是第 k 层的所有节点必须集中在最左边。
简单地说, 就是叶子节点都必须在最后一层或者倒数第二层,而且必须在左边。任何一个节点都不能没有左子树却有右子树。
- 满二叉树
如果一棵树的高度为 k,且拥有 2^k-1 个节点,则称之为 满二叉树。
就是说,每个节点要么必须有两棵子树,要么没有子树。
- 满二叉树 和 完全二叉树 的对比图
教材学习中的问题和解决过程
- 问题:链式二叉树中的
find方法只能用在contain方法里,能不能返回一个BinaryTreeNode对象 ,便于往树中添加新的元素 - 问题解决方案:
1.find方法源代码
public T find(T targetElement) {
BinaryTreeNode<T> current = findNode(targetElement, root);
if (current == null)
throw new ElementNotFoundException("LinkedBinaryTree");
return (current.getElement());
}
返回BinaryTreeNode对象的find方法代码
public BinaryTreeNode<T> findNode(T targetElement) {
BinaryTreeNode<T> current = findNode(targetElement, root);
if (current == null)
throw new ElementNotFoundException("LinkedBinaryTree");
return current;
}
2.经过对代码的深入理解发现这种方法并不可行,因为这样新加入的元素并不能是一个单独的LinkedBinaryTree(链式二叉树)对象,只是一个BinaryTreeNode(二叉树结点)对象,这样会导致新插入的元素不能使用链式二叉树类里的方法。
代码调试中的问题和解决过程
-
问题:背部诊断器类运行时一直报错
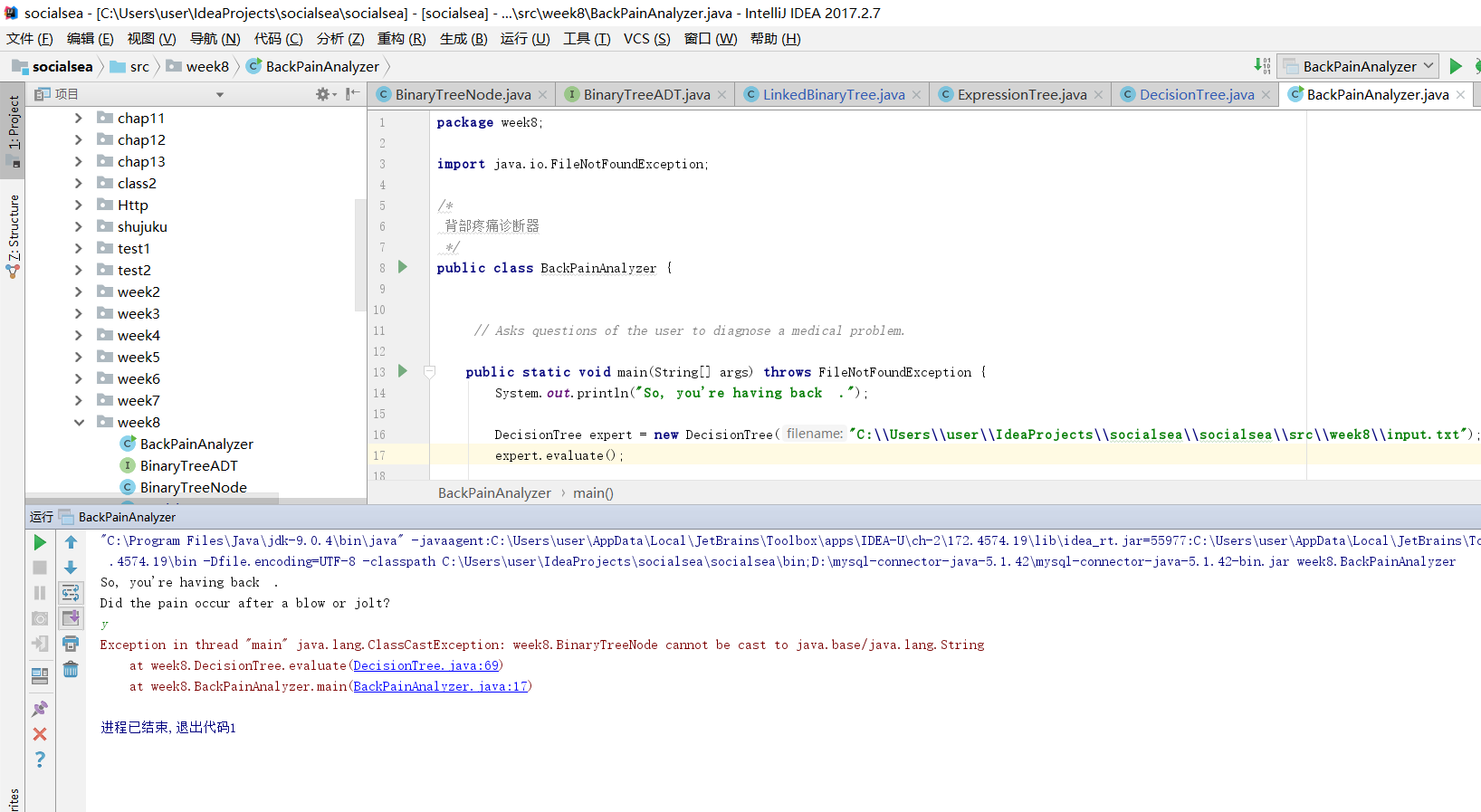
-
问题解决方案:
经过单步调试发现是因为我的LinkedBinaryTree类里的getLeft方法和getRight方法返回的是BinaryTreeNode对象而不是LinkedBinaryTree对象,
对两个方法进行修改后终于使问题得到解决
1.修改前的getLeft方法和getRight方法代码
//返回结点的左侧子结点
public BinaryTreeNode<T> getLeft() {
return left.root;
}
//返回结点的右侧子结点
public BinaryTreeNode<T> getRight() {
return right.root;
}
- 修改后的
getLeft方法和getRight方法代码
public LinkedBinaryTree<T> getLeft() {
return left.root;
}
//返回结点的右侧子结点
public LinkedBinaryTree<T> getRight() {
return right.root;
}
代码托管

上周考试错题总结
上周无错题!!!
结对及互评
- 本周结对学习情况
本周主要对链式二叉树进行了较为深入的学习,在学习的过程中遇到了诸多较难的问题,有的问题我们两个也是都摸不着头脑,但是通过查阅相关的资料最终使问题得到了解决!
感想
本周的主要学习内容是对树的概念进行了较为深入的了解,并且对链式二茬表的实现进行了学习和实现,本章课本的例题代码比较复杂(对我来说很复杂了),在阅读代码的过程中也是花费了不少时间,通过对本章的学习也是认识到了我的阅读代码能力还是很差的!希望以后继续努力,让自己在这方面的能力有所提高吧!
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 0/0 | 1/1 | 4/4 | |
| 第二周 | 464/464 | 1/2 | 10/14 | 理解掌握了用数组和链表实现栈的方法 |
| 第三周 | 494/958 | 1/3 | 10/24 | 理解掌握了用数组和链表实现队列的方法 |
| 第四周 | 1629/2587 | 2/5 | 20/44 | 对用链表和数组实现列表进行了学习 |
| 第五周 | 856/3443 | 2/7 | 15/59 | 较为深入的学习了查找和排序方法的实现 |
| 第六周 | 668/4111 | 1/8 | 20/79 | 学习了链式二叉树的实现 |
-
计划学习时间:20小时
-
实际学习时间:20小时
-
改进情况:注重提高阅读复杂代码的能力,努力提高解决代码bug的能力!!!





