小学生四则运算（java编程）201571030135

任务1源码在Github的仓库主页链接地址：

https://github.com/zhanghh2018/Four-primary-school-pupils

需求分析：

作业总体效果：随机产生n道加减乘除练习题；
练习题的构成：数字和运算符且每个数字在 0 和 100 之间，运算符在3个到5个之间且每个练习题至少要包含2种运算符；
练习题的结果：练习题在运算过程中不出现负数与非整数；
最终提交结果：学号与生成的n道练习题及其对应的正确答案；样例如下：

功能设计：

表达式的生成模块。首先需要生成运算符与数字，每个等式中运算符的个数加一就等于该等式中的数字个数，之后将生成的符号与数字组合成String,传入逆波兰计算模块进行结果的输出。在此模块中将除法中分母为零的情况、运算符只有一种的情况以及分子分母除不尽的情况排除。
表达式的计算模块。利用逆波兰表达式计算结果，在该模块中排除例如30/6/3这样的情况，在之前的模块中排除的只是除号前后的分子分母的情况，并未考虑除号连续的情况，当除号连续时，需要考虑第一个除号运算完之后的结果能否继续除以下一个数的情况，当遇到前后余数不为0的情况以及中间结果为负数的情况就跳出该函数，继续产生新的等式直至满足条件。写这个模块的时候借鉴这位博主的写法（http://blog.csdn.net/u010485491/article/details/51483720）；
结果写入文件模块。将自己的学号与根据用户输入的题目个数生成的等式写入文件。
异常情况的处理。排除输入为非数字的情况以及输入的数字大于1000、小于1以及等于0的情况。

基本功能：

实现每道练习题运算符在3个到5个之间，至少要包含2种运算符；
运算结果无负数以及非整数；
将最终结果保存在文档中以样例为模板；
每道练习题的结果不超过一定的范围（考虑到小学生计算能力有限，当时问了郑老师，在老师的提示下，设置了用户输入想要生成结果的范围这一块内容，并进行了异常处理）。

设计实现：

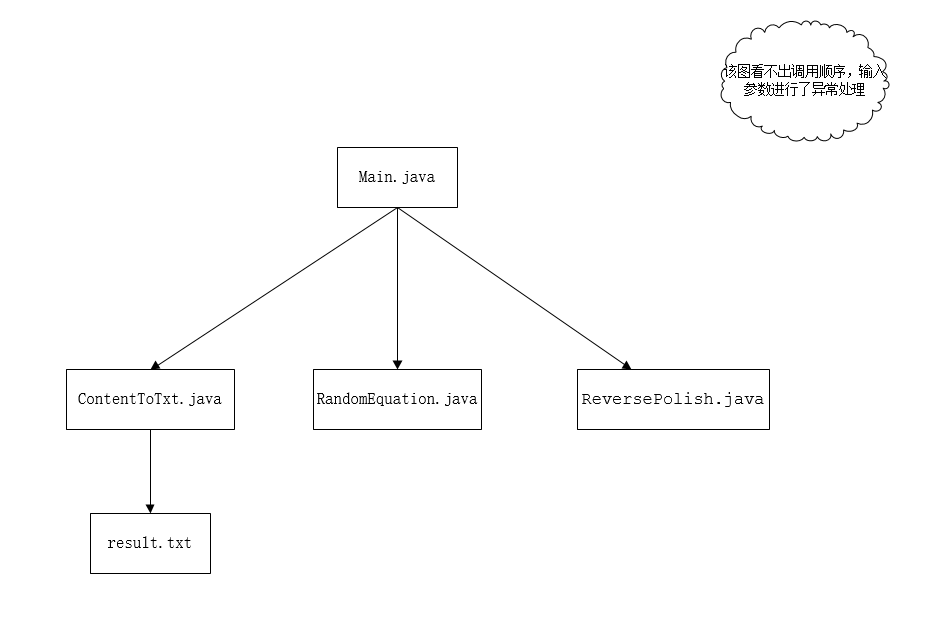
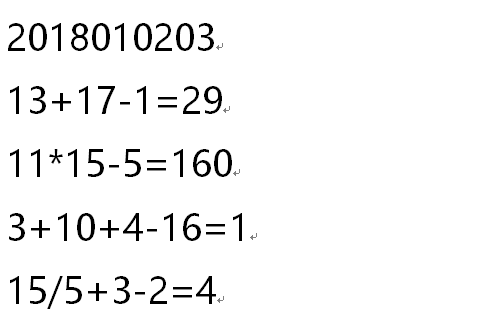利用Visio进行流程图的绘制，具体流程图如下：其中ContentToTxt(将结果写入文件) Main(主程序可以从命令行接收参数) ReversePolish (逆波兰表达式) RandomEquation(产生等式) result.txt(运行后产生的结果)

测试运行：

核心代码：

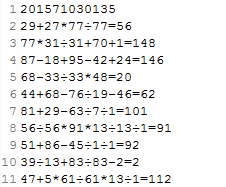
1）随机产生等式模块：为了看起来整洁，去掉了测试过程中注释掉的打印输出部分。等式生成是将生成的数字与运算符依次拼接，之后加上等号构成等式，在构建过程中去除运算符只有一种的情况、分母为0的情况，分子分母有余数的情况。

  1 public class RandomEquation {
  2     public static String randomEquation (){
  3         
  4         // Previous expressions
  5         
  6         String sBefore = new String();
  7         
  8         // The later expression
  9         
 10         String sLater = new String();
 11         char[] equation;
 12         int k = 6;
 13         int n;
 14         int m;
 15         int j;
 16         int i;
 17         int[] number;
 18         char[] symbol;
 19         number = new int[k];
 20         symbol = new char[k];
 21         equation = new char[2 * k];
 22         char[] cSymbol = {'+','-','*','÷'};
 23         Random random = new Random();
 24         
 25         // Generating operator
 26         
 27         for(i = 0;i<(int)(Math.random()*3)+3;i++){
 28             int index = random.nextInt(cSymbol .length); 
 29             char resultChar = cSymbol[index];
 30             symbol[i] = resultChar;
 31             
 32         }
 33         for(m = 0;m < i;m++){
 34             if(symbol[i - 1] != symbol[m]){
 35                 break;
 36             }
 37         }
 38         
 39         /*
 40          * Removal of only one operator
 41          * If the last symbol is the same as the previous one, the last one generates a symbol at random.
 42          */
 43         
 44         if(m == i){
 45             do{
 46                 int index = random.nextInt(cSymbol.length); 
 47                 char resultChar = cSymbol[index];
 48                 symbol[i - 1] = resultChar;
 49             }while(symbol[i - 1] == symbol[i - 2]);
 50         }
 51         
 52         // Generating number
 53         
 54         for(j = 0;j < i + 1;j++){
 55                 
 56             int num = (int)(Math.random()*100);
 57             number[j] = num;
 58             
 59         }
 60         
 61         // Generating equation
 62         
 63         for(n = 0;n < i;n++){
 64             sBefore += String.valueOf(number[n])+String.valueOf(symbol[n]);
 65         }
 66         sBefore += String.valueOf(number[i]);
 67     
 68         // Save symbols and numbers into a equation array 
 69         
 70         for(n = 1;n < 2 * i;n = n+2){
 71             
 72             equation[n] = symbol[(n - 1) / 2];
 73         }
 74         for(n = 0;n < 2 * j - 1;n = n+2){
 75             
 76             equation[n] = (char)number[(n + 1) / 2];
 77             
 78         }
 79        
 80       // The removal ÷ denominator is 0 and the molecular denominator is incompatible
 81         
 82         for(n = 1;n < i + j && n + 1 < i + j;n = n + 2){
 83             if(equation[n] == '÷'){
 84                 if(equation[n + 1]==0){
 85                     do{
 86                         int num2 = (int)(Math.random()*100);
 87                         equation[n + 1] = (char)num2;
 88                     }while(equation[n + 1] == 0);
 89                 }
 90                 else if((int)equation[n - 1] % (int)equation[n + 1]!=0 || (int)equation[n - 1]<(int)equation[n + 1]){
 91                     do{
 92                         
 93                         int num2 = (int)(Math.random()*100) + 1;
 94                         equation[n + 1] = (char)num2;
 95                         if(equation[n + 1] == 0){
 96                             do{
 97                                 int num3 = (int)(Math.random()*100);
 98                                 equation[n + 1] = (char)num3;
 99                             }while(equation[n + 1] == 0);
100                         }
101                         
102                     }while((int)equation[n - 1] % (int)equation[n + 1]!= 0 || (int)equation[n - 1]<(int)equation[n + 1]);
103                 }
104                 
105             }
106             
107             
108         }
109         // The equation after excluding special circumstances
110         
111         for(n = 0;n < i+j && n + 1 < i + j;n = n + 2){
112             
113             sLater += String.valueOf((int)equation[n]);
114             sLater += String.valueOf(equation[n + 1]);
115             
116         }
117         sLater += String.valueOf((int)equation[i + j - 1]);
118         sLater += String.valueOf('=');
119        
120         return sLater;
121     }
122     
123 }

2）逆波兰模块借鉴这位博主的写法，并在理解的基础上进行了代码的加工。当中间结果小于0或者a%b!=0时，利用return跳出该函数，并在下边的模块中利用返回值进行等式的重新生成。 http://blog.csdn.net/u010485491/article/details/51483720

 1 public static int calcInt(int a, int b, String stmp) 
 2     {
 3         int res = 0;
 4         char s = stmp.charAt(0);
 5         switch (s) {
 6           case '+': {
 7             res = a + b;
 8             break;
 9           }
10           case '-': {
11             res = a - b;
12             if(res < 0){
13                 return -1;
14             }
15             break;
16           }
17           case '*': {
18             res = a * b;
19             break;
20           }
21           case '÷': {
22             res = a / b;
23             if( a % b != 0){
24                 return -1;
25             }
26             break;
27           }
28         }
29         return res;
30     }

3）结果写入文件模块，由于随机产生等式,所以需要一直将该等式保存到字符串里，并对该字符串进行逆波兰求解，否则若随机产生式子randomEquation()，之后又利用ReversePolish(randomEquation()))产生的随机等式的结果，这样会出现等式计算结果与最终运算结果不匹配的情况。在该模块中利用返回值的不同进行结果的保存，若返回值为-1或者大于用户输入的结果值result，就将i的值自减，这样就相当于重新产生符合条件的式子。

 1 for(int i = 0;i < questionAmount;i++){
 2             
 3             String randoms = randomEqual.randomEquation();
 4             final boolean existed = reversePolish.reversePolish(randoms) != -1 && reversePolish.reversePolish(randoms) < 500;
 5             if(existed){
 6                 
 7                 contentToTxt.contentToTxt(strFilePath,String.valueOf(randoms+reversePolish.reversePolish(randoms)));
 8                 contentToTxt.contentToTxt(strFilePath,String.valueOf("\n"));
 9             }else{
10                 i--;
11             }
12         }

总结：

在拿到题目的时候，并没有急着去完成代码而是首先进行了需求分析，根据需求分析将本次作业分为三大模块，并对这三个模块进行了功能的划分，每个模块都有要实现的功能，且尽量降低模块之间的联系。以这样的做法书写下来发现思路很清晰，由于不再在一个函数体内书写程序，一个模块出了问题不必全篇找，直接在这个模块中修改即可。
由于参加完蓝桥杯之后就没有与java打交道了，一直与c语言打交道，所以java当中的语法也遗忘了不少，使用new这一关键字创建对象也给忘记啦，突然想到一则笑话（甲说都大三了，连女朋友都没有。乙说：new一个‘对象’），这下子就忘不了啦。
在书写代码的过程中使用了do while语句，不需要判断循环次数，以前一直在使用while语句，这次在产生表达式的过程中大量使用了do while,深刻体会到了该语句的妙处。
在考虑情况的时候并不是一次性完成的，而是在编写代码的过程中慢慢想出来的，到了最后计算结果的时候发现结果已经有上万的啦，所以将输出结果限制在用户要求的范围内，这样就和小学生实际情况相符合。
在生成表达式中去除分子分母不能整除的时候，例如a/b/c判断,若a/b不能整除就再随机产生a,b;若同时b/c不能整除则再随机产生b,c;这样下来发现会产生a/b不能整除的情况，因为b随机了两次，后一次随机就无法保证a/b是整数了，所以想到在逆波兰计算的时候进一步排除连续除号除不尽的情况。
最后写的是文件模块，由于是将之前写的文档import进去的，在测试是否写好文件的时候发现在目录JRE System Library下边没有产生文件，最后在打开的文件夹中找到了，所以之后的每一次运行就拿Windows自带的记事本打开，明明写了换行符但仍在一行上，测试了好几次都不对，最后和同学交流了才发现这个问题，利用notepad++打开结果就是合适的。
本来是想进行附加功能的添加，然而做的时候将一些特殊请款考虑到生成表达式的模块中，导致这些附加功能无法实现，比如真分数的计算，在生成表达式的过程中，将分子分母除不尽的情况已经排除，另外就是加括号的情况，在此模块中将除法中出现的分母为零的情况排除，排除的时候只看除号后边的数字，如果加上括号就没办法进行特殊情况的判断。所以还是在写的时候全盘考虑，不能只想着实现这些基本功能，使得算法没有拓展性。

PSP：

PSP2.1	任务内容	计划完成需要的时间(min)	实际完成需要的时间(min)
Planning	计划	20	25
Estimate	估计这个任务需要多少时间，并规划大致工作步骤	20	25
Development	开发	360	418
Analysis	需求分析 (包括学习新技术)	10	10
Design Spec	生成设计文档	10	8
Design Review	设计复审 (和同事审核设计文档)	10	15
Coding Standard	代码规范 (为目前的开发制定合适的规范)	20	20
Design	具体设计	30	35
Coding	具体编码	240	280
Code Review	代码复审	20	25
Test	测试（自我测试，修改代码，提交修改）	20	25
Reporting	报告	20	27
Test Report	测试报告	5	5
Size Measurement	计算工作量	5	12
Postmortem & Process Improvement Plan	事后总结 ,并提出过程改进计划	10	10

posted on 2018-03-20 18:11 阳阳2018 阅读(1375) 评论(2) 编辑收藏举报