js实现数据结构的基本算法

　　之前一提到数据结构与算法感觉这应该是后端要掌握的知识，对我们前端来说只要写写页面，绑定事件，向后台发发数据就好了，用不到数据结构与算法，即使是用到算法也有一些js的api可以实现，也许对于一些数据查找 简单的for循环就能搞定，也只是提高了几毫秒而已完全可忽略不计，但是假如node做后台开发的时候， 一次请求节约的几毫秒，千万次请求节约的就不是毫秒来计算了。看看人家那些大牛们，我这样的小白想当老白啊，所以基本的算法以及对数据结构的掌握这是向他们靠近必须要走的路。今天先来回顾一下大学学的基本算法吧也是必须掌握的基本算法。

　　还好数据结构是在毕业的时候唯一没被卖掉的书，翻了翻书看到算法的定义：

　　①算法的特征：有穷性、确定性、可行性、输入、输出

　　②算法的设计衡量：正确性、可读性、健壮性, 时间复杂度, 空间复杂度

基本算法：

　　1.冒泡排序：

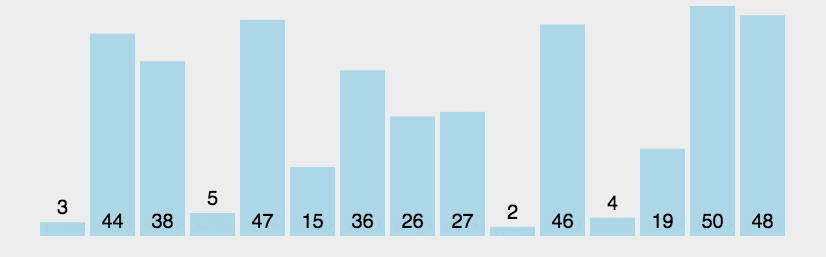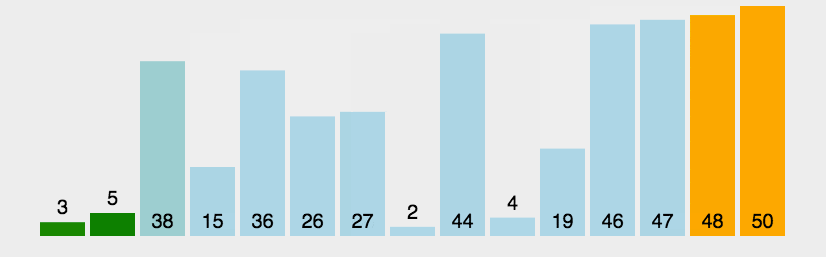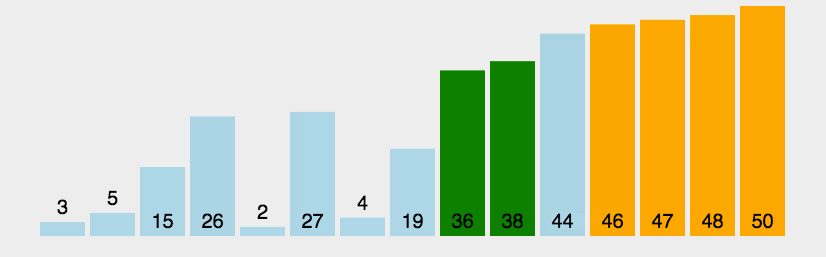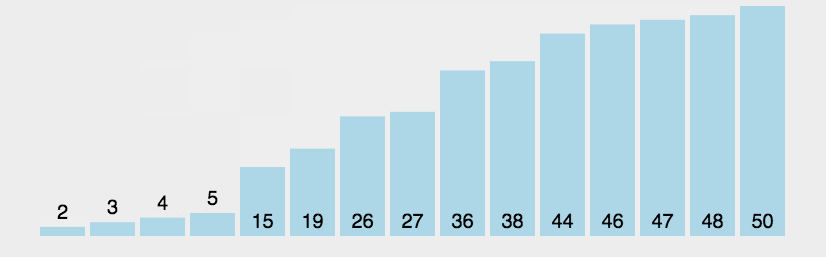
　　1.原理：比较两个相邻的元素，将值大的元素交换到右边

　　2.思路：依次比较相邻的两个数，将比较小的数放在前面，比较大的数放在后面。

　　　　(1)第一次比较：首先比较第一和第二个数，将小数放在前面，将大数放在后面。

　　　　(2)比较第2和第3个数，将小数 放在前面，大数放在后面。

　　　　......

　　　　(3)如此继续，直到比较到最后的两个数，将小数放在前面，大数放在后面，重复步骤，直至全部排序完成

　　　　(4)在上面一趟比较完成后，最后一个数一定是数组中最大的一个数，所以在比较第二趟的时候，最后一个数是不参加比较的。

　　　　(5)在第二趟比较完成后，倒数第二个数也一定是数组中倒数第二大数，所以在第三趟的比较中，最后两个数是不参与比较的。

　　　　(6)依次类推，每一趟比较次数减少依次

function bubbleSort(arr) {
    var len = arr.length;
    for (var i = 0; i < len - 1; i++) {//外层控制循环多少趟，
        for (var j = 0; j < len - 1 - i; j++) {//内层控制每一趟的循环次数
            if (arr[j] > arr[j+1]) {        // 相邻元素两两对比
                var temp = arr[j+1];        // 元素交换
                arr[j+1] = arr[j];
                arr[j] = temp;
            }
        }
    }
    return arr;
}

　　2.快速排序：

　　

　　1.算法思想
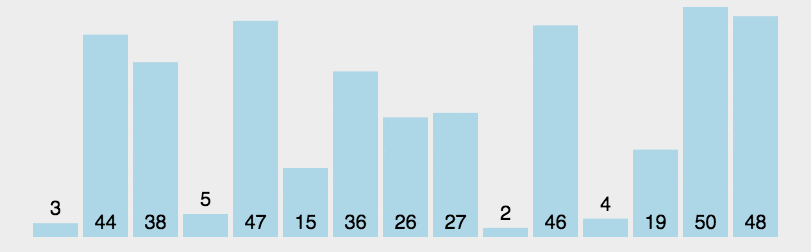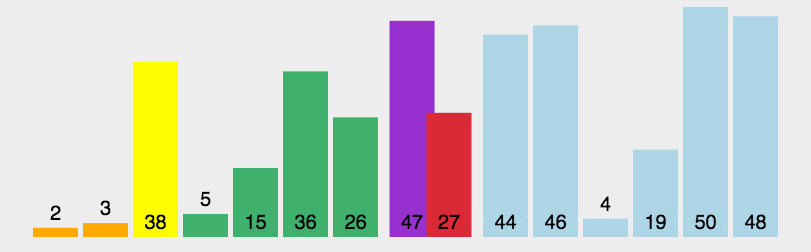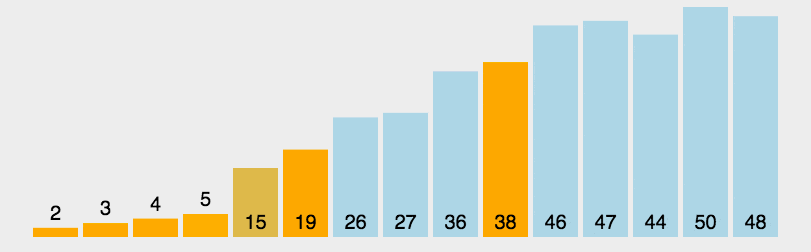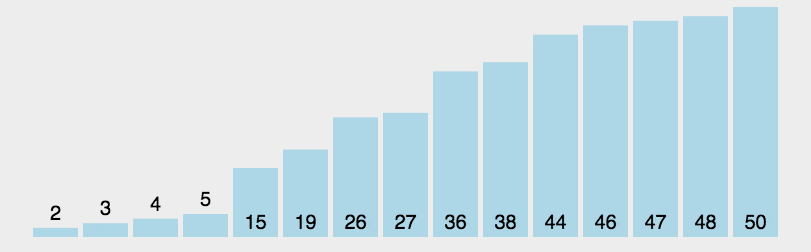
　　   快速排序的基本思想：通过一趟排序将待排记录分隔成独立的两部分，其中一部分记录的关键字均比另一部分的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序。

　　2.实现原理

　　(1)设置两个变量 low、high，排序开始时：low=0，high=size-1。
　　(2)整个数组找基准正确位置，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面

　　(3)默认数组的第一个数为基准数据，赋值给key，即key=array[low]。

　　(4)因为默认数组的第一个数为基准，所以从后面开始向前搜索（high–），找到第一个小于key的array[high]，就将 array[high] 赋给 array[low]，即 array[low] = array[high]。（循环条件是 array[high] >= key；结束时 array[high] < key）

　　(5)此时从前面开始向后搜索（low++），找到第一个大于key的array[low]，就将 array[low] 赋给 array[high]，即 array[high] = array[low]。（循环条件是 array[low] <= key；结束时 array[low] > key）

　　(6)循环 4-5步骤，直到 low=high，该位置就是基准位置。

　　(7)把基准数据赋给当前位置。

function swap(items, firstIndex, secondIndex){
    var temp = items[firstIndex];
    items[firstIndex] = items[secondIndex];
    items[secondIndex] = temp;
}

function partition(items, left, right) {
    var pivot = items[Math.floor((right + left) / 2)],
        i = left,
        j = right;
    while (i <= j) {
        while (items[i] < pivot) {
            i++;
        }
        while (items[j] > pivot) {
            j--;
        }
        if (i <= j) {
            swap(items, i, j);
            i++;
            j--;
        }
    }
    return i;
}

function quickSort(items, left, right) {
    var index;
    if (items.length > 1) {
        index = partition(items, left, right);
        if (left < index - 1) {
            quickSort(items, left, index - 1);
        }
        if (index < right) {
            quickSort(items, index, right);
        }
    }
    return items;
}

var items = [3,8,7,2,9,4,10]
var result = quickSort(items, 0, items.length - 1);

　　3.插入排序

　　1.原理

　　将一组数据分成俩组，暂时叫做有序组和待插入组。每次从待插入组中取出一个元素，与有序组的元素进行比较，并找到合适的位置，将该元素插到有序组当中。就这样，每次插入一个元素，有序组增加，待插入组减少。直到待插入组元素个数为0。当然，插入过程中涉及到了元素的移动。

　　2.过程

　　　（1）将数组的第一个数作为有序组，其他数作为待插入组

　　　（2）从待插入组依次与有序组中的数进行对比，在合适位置插入

　　　（3）直到待插入组为空

 

function insertionSort(arr) {
    var len = arr.length;
    var preIndex, current;
    for (var i = 1; i < len; i++) {//从1开始，数组从第二个数开始作为待插入组
        preIndex = i - 1;
        current = arr[i];
        while(preIndex >= 0 && arr[preIndex] > current) {
            arr[preIndex+1] = arr[preIndex];
            preIndex--;
        }
        arr[preIndex+1] = current;
    }
    return arr;
}

　　4.选择排序

　　1.原理

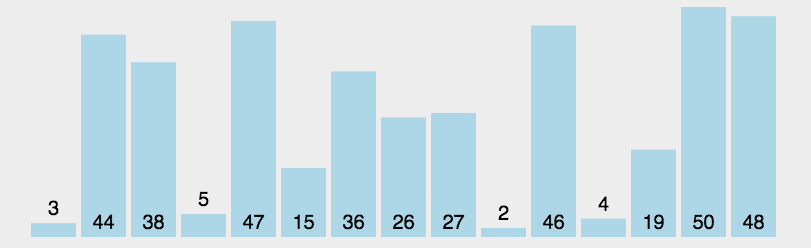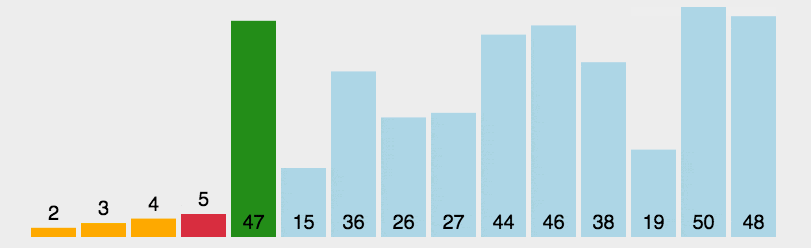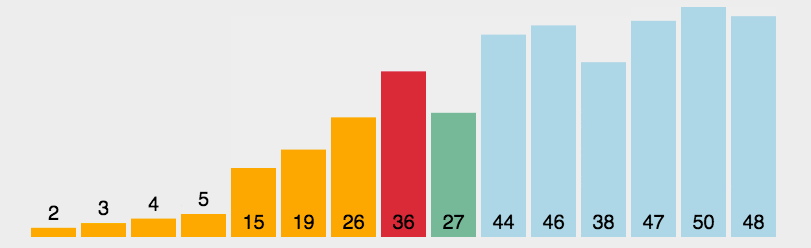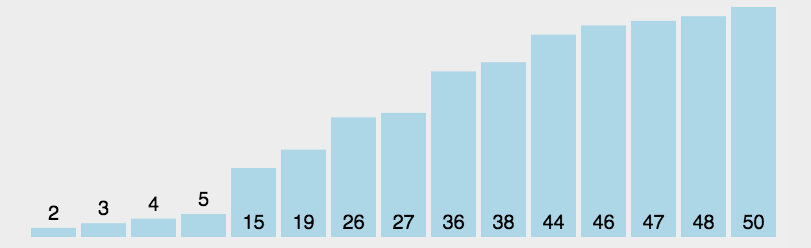
　　选择排序改进了冒泡排序，每次遍历列表只做一次交换，为了做到这一点，一个选择排序在遍历时寻找最大(小)的值，并在完成遍历后，将其放到正确的地方。

　　2.过程

　　（1）第一轮从arr[0]~arr[n-1]中找到最小的元素，与arr[0]进行交换；
　　（2）第二轮从arr[1]~arr[n-1]中找到最小的元素，与arr[1]进行交换；
　　　　…
　　（3）依次类推，经过n-1轮之后，就形成了有序序列

function selectionSort(arr) {
    var len = arr.length;
    var minIndex, temp;
    for (var i = 0; i < len - 1; i++) {
        minIndex = i;
        for (var j = i + 1; j < len; j++) {
            if (arr[j] < arr[minIndex]) {     // 寻找最小的数
                minIndex = j;                 // 将最小数的索引保存
            }
        }
        temp = arr[i];
        arr[i] = arr[minIndex];
        arr[minIndex] = temp;
    }
    return arr;
}

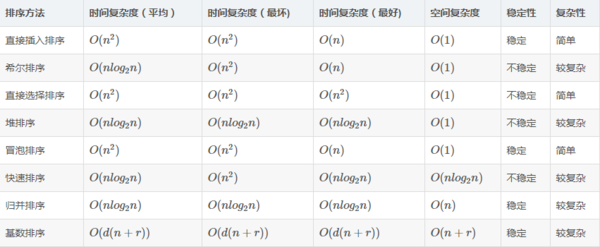
　　5.时间复杂度空间复杂度对比

　　　在冒泡排序，插入排序，选择排序，快速排序中，在最最坏情况下，快速排序的时间复杂为O(n2) ，插入排序O(n2)，选择排序O(n2)，冒泡排序O(n2)