动态规划DP

70. 爬楼梯

You are climbing a stair case. It takes n steps to reach to the top.

Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?

Example 1:

Input: 2
Output: 2
Explanation: There are two ways to climb to the top.
1. 1 step + 1 step
2. 2 steps

Example 2:

Input: 3
Output: 3
Explanation: There are three ways to climb to the top.
1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 steps + 1 step

class Solution:
    def climbStairs(self, n: int) -> int:
        memo = [1,1]
        if n <= 2 :return n 
        for i in range(2,n+1):
            memo.append(memo[i-1] + memo[i-2])
        return memo[n]

个人理解：

暴力法时间2的n次，空间n：DFS设立终止条件当步数大于等于楼数返回，爬n层楼梯取决于n-1层和n-2层楼梯方法之和，爬n-1取决于n-2和n-3以此类推...爬2层楼梯的方法有2种，爬1层楼梯的方法有1种,返回结果；

 

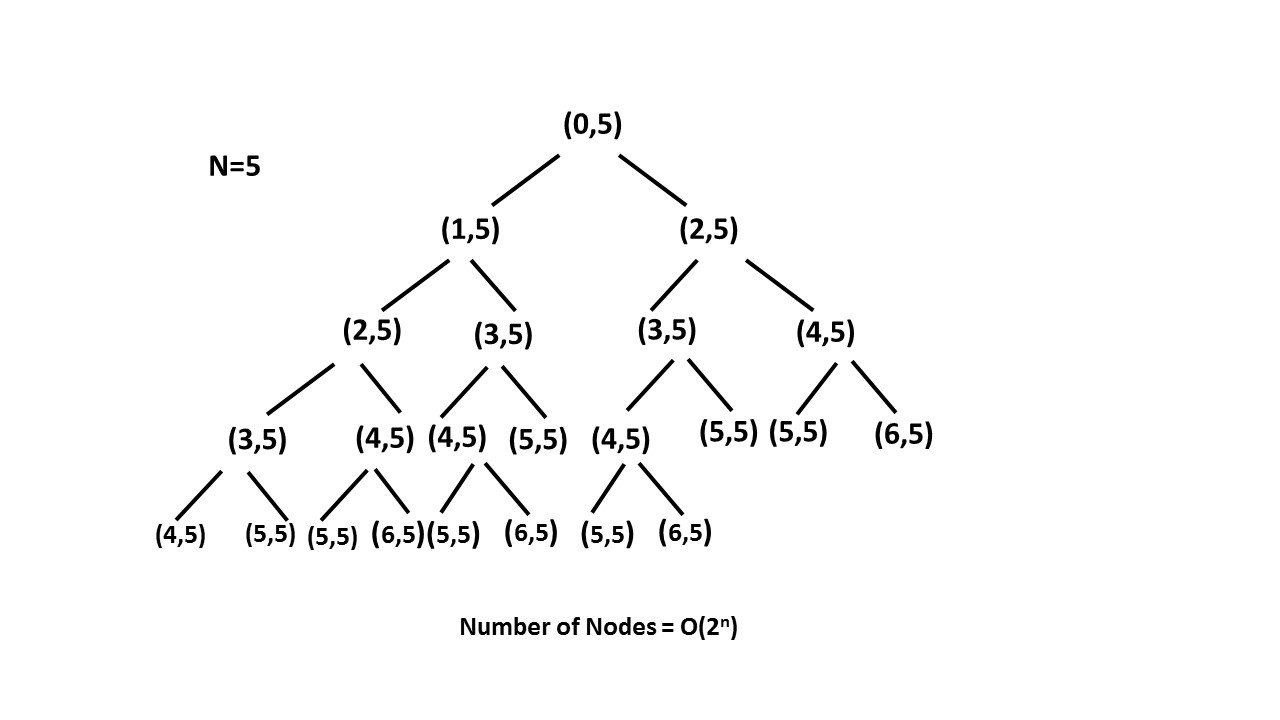
回溯 O(n)：每次记录层数的值并传递到下一层，可以节省重复计算的时间；

递推 O(n)：状态dp[1]=1,dp[2]=2，转移方程dp[i] = dp[i - 1] + dp[i - 2]

 

120. Triangle

Given a triangle, find the minimum path sum from top to bottom. Each step you may move to adjacent numbers on the row below.

For example, given the following triangle

[
     [2],
    [3,4],
   [6,5,7],
  [4,1,8,3]
]

class Solution:
    def minimumTotal(self, triangle: List[List[int]]) -> int:
        t = triangle
        if t == '':return 0
        self.dp={}
        return self._dfs(t,0,0)

                    
    def _dfs(self,_t,x,y):
        if x >= len(_t):return 0
        if (x,y) not in self.dp:
            mini = min(self._dfs(_t,x+1,y),self._dfs(_t,x+1,y+1))
            self.dp[(x,y)] = _t[x][y] + mini
        return self.dp[(x,y)]

class Solution:
    def minimumTotal(self, triangle: List[List[int]]) -> int:
        t = triangle
        if not t: return 0
        
        res=t[-1]
        
        for i in range(len(t)-2,-1,-1):  
            for j in range(len(t[i])):  
                    res[j]=min(res[j],res[j+1])+t[i][j]
                    
        return res[0]

个人理解：

递归：从上往下，以元组的形式记录路径字典下标，判断(x+1,y)与(x+1,y+1)之间较小者，带到下一层

递推：从下往上推断，定义DP[i，j]二维数组，起始值为最后一行，i范围为倒数第二行开始到0 range(len(t)-2,-1,-1)，j范围为最后一行，转移方程res[j]=min(res[j],res[j+1])+t[i][j]，选择最后一行较小值加上倒数第二行本身

 

 

 

152. 乘积最大子序列

Given an integer array nums, find the contiguous subarray within an array (containing at least one number) which has the largest product.

Example 1:

Input: [2,3,-2,4]
Output: 6
Explanation: [2,3] has the largest product 6.

Example 2:

Input: [-2,0,-1]
Output: 0
Explanation: The result cannot be 2, because [-2,-1] is not a subarray.

 

class Solution:
    def maxProduct(self, nums: List[int]) -> int:
        if nums == '':return 0
        dp = [[0 for _ in range(2)] for _ in range(2)]
        dp[0][0],dp[0][1],res = nums[0], nums[0],nums[0]
        
        for i in range(1,len(nums)):
            x,y = i%2, (i-1)%2
            dp[x][0] = max(dp[y][0]*nums[i],dp[y][1]*nums[i],nums[i])
            dp[x][1] = min(dp[y][0]*nums[i],dp[y][1]*nums[i],nums[i])
            res = max(res,dp[x][0])
        return res

个人理解：

递推：定义状态DP 2X2 二维数组来记录乘或者不乘的结果，初始值都为第一个值，dp[x]记录当前位置，dp[y]为前一个位置，dp[x][0]记录最大值，dp[x][1]记录最小值，0,1 1,0循环使用x,y = i%2, (i-1)%2

转移方程

dp[x][0] = max(dp[y][0]*nums[i],dp[y][1]*nums[i],nums[i])
dp[x][1] = min(dp[y][0]*nums[i],dp[y][1]*nums[i],nums[i])

if a[i]>0 : dp[i][0] = dp[i-1][0]*a[i]　　else : dp[i][0] = dp[i-1][1]*a[i] 

if a[i]>0 : dp[i][1] = dp[i-1][1]*a[i]　　else : dp[i][1] = dp[i-1][0]*a[i] 

 

 

 

300. 最长上升序列

Given an unsorted array of integers, find the length of longest increasing subsequence.

Example:

Input: [10,9,2,5,3,7,101,18]
Output: 4 
Explanation: The longest increasing subsequence is [2,3,7,101], therefore the length is 4.

 

class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        if len(nums) == 0: return 0
        dp = len(nums) * [1]
        res=1
        for i in range(len(nums)):
            for j in range(0,i):
                if nums[j] < nums[i]:
                    dp[i] =max(dp[i],dp[j]+1)
            res = max(res,dp[i])
        return res

class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        if len(nums) == 0: return 0
        dp = len(nums) * [0]
        size = 0
        for k in nums:
            i,j = 0,size
            while i!=j:
                m = (i+j)//2
                if dp[m] < k:
                    i = m+1
                else:
                    j = m
            dp[i] = k
            size = max(i+1,size)
        return size

个人理解：

暴力法复杂度为n方：递归往下查找，记录取值和不取值的情况，再往下深入，当位置为长度时终止，最后返回取值和不取值中的最大值；

递推复杂度时间n方、空间为n：dp状态定义开一个数组记录相加次数，转移方程为dp[i] =max(dp[i],dp[j]+1)，当原数组当前值比前值大时，在dp中比较当前值的dp数和前值dp数+1哪个大，一层循环后记录本层结果较大值res = max(res,dp[i])，意思是在这之前的有比当前值小的情况dp+1，而比较max可以规避比当前值小但比再前值大的情况；

二分法时间(nlogn)，空间为n：开dp空间，遍历数组，当中间数dp[m]小于当前值时取右边i=m+1，否则取左边j=m，意思是假如当前值为更小值，替换掉该位置的dp值，假如当前值为大值，移动到i位，插入新值，插入值越小后续插入值机会越多，size控制在size = max(i+1,size)；

 

 

322.零钱兑换

You are given coins of different denominations and a total amount of money amount. Write a function to compute the fewest number of coins that you need to make up that amount. If that amount of money cannot be made up by any combination of the coins, return -1.

Example 1:

Input: coins = [1, 2, 5], amount = 11
Output: 3 
Explanation: 11 = 5 + 5 + 1

Example 2:

Input: coins = [2], amount = 3
Output: -1

class Solution:
    def coinChange(self, coins: List[int], amount: int) -> int:
        if amount < 1 :return 0
        k=[0]*amount
        return self._dp(coins,amount,k)
    
    def _dp(self,coins,rem,count):
        if rem<0:return -1
        if rem == 0 : return 0
        if count[rem-1]!=0:return count[rem-1]
        mini = 100
        for coin in coins:
            res = self._dp(coins,rem-coin,count)
            if (res>=0 and res<mini):
                mini = 1+res
        count[rem-1] = -1 if mini == 100 else mini
        return count[rem-1]

class Solution:
    def coinChange(self, coins: List[int], amount: int) -> int:
        dp = [float('inf')] * (amount + 1)
        dp[0] = 0
        
        for coin in coins:
            for x in range(coin, amount + 1):
                dp[x] = min(dp[x], dp[x - coin] + 1)
        return dp[amount] if dp[amount] != float('inf') else -1 

个人理解：

首先想到暴力法，枚举各个硬币所能兑换的钱数以及各硬币结果合并，所兑换的次数最小者为答案；

DFS找下一层，将需要求解的值x-coin和count记录数带到下层，返回最小的次数，当rem为0时返回0，count[rem-1]不为0则返回

其次是动态规划，先DP状态定义，新开一个dp组默认值为inf来表示次数，转移方程为DP[x]=min(DP[x],DP[x-coin[j]]+1)

当dp组内数字为改变时说明amount无法由coins组成，返回-1，否则返回最后一个dp值，每一个dp值为上一个数兑换硬币后计算