C++ 点的线性拟合 y(x)=ax+b

一、简单分析

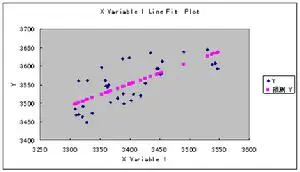
　　点的线性拟合是一般实验数据处理最常用的方法。下面考虑一个用n个数据点拟合成直线的问题，直线模型为

y(x)=ax+b

　　这个问题称为线性回归。设变量y随自变量x变化，给定n组观测数据（xi,yi），用直线来拟合这些点，其中a,b是直线的斜率和截距，称为回归系数。

　　为确定回归系数，通常采用最小二乘法，即使下式达到最小

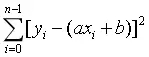
　　 根据极值愿意，a,b满足下列方程

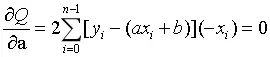
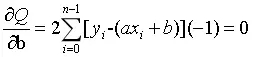
 　　可解得：

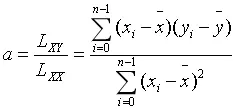
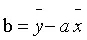
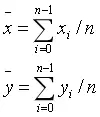
 　　最终可得直线方程

y(x)=ax+b

　　对于任何一组数据，都可以用这种方式拟合出一条直线，而数据点有些远离直线，有些接近直线，便有一个系数作为对所拟合直线的线性程度的一般判据

　　它可以判断一组数据线性相关的密切程度

　　定义为：

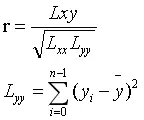
　　r的绝对值越接近与1，表示直线的线性关系越好，直线关系的数据r=1。

二、代码实现

#ifndef _POINT_H
#define _POINT_H_

class Point {
    public:
        Point(float x=0,float y=0):x(x),y(y) {};
        float getX() {return x;}
        float getY(){return y;}
    private:
        float x,y; 
};

#endif

#include "Point.h"
#include<iostream>
#include<math.h>

using namespace std;

//直线线性拟合 points为点 n为点的个数
void lineFit(Point points[],int n) {
    float avgX,avgY=0;
    float Lxx=0,Lyy=0,Lxy=0;

    //计算x,y平均值
    for(int i=0; i<n; i++) {
        avgX+=points[i].getX()/n;
        avgY+=points[i].getY()/n;
    }

    //计算Lxx,Lyy,Lxy
    for(int i=0; i<n; i++) {
        Lxy += (points[i].getX()-avgX)*(points[i].getY()-avgY);
        Lxx += (points[i].getX()-avgX)*(points[i].getX()-avgX);
        Lyy += (points[i].getY()-avgY)*(points[i].getY()-avgY);
    }

    cout<<"*--线性拟合结果如下--*"<<endl;
    float a = Lxy/Lxx;
    cout<<"a="<<a<<endl;
    float b = avgY-a*avgX;
    cout<<"b="<<avgY-a*avgX<<endl;
    cout<<"相关系数r="<<Lxy/sqrt(Lxx*Lyy)<<endl;
    cout<<"线性方程:"<<"y="<<a<<"+"<<b<<"x"<<endl;
}

int main() {
    Point p[5] = {
        Point(6,10),
        Point(5,12),
        Point(7,10),
        Point(5,10),
        Point(6,8)
    };

    lineFit(p,5);

    cout<<endl<<"测试2"<<endl;

    Point p_line[3] = {
        Point(6,10),
        Point(6,11),
        Point(7,12)
    };

    lineFit(p_line,3);
    return 0;
}