双线性插值
原理:
那么对于浮点数的坐标(x,y)满足(a<=x<a+1,b<=y<b+1),我们可以先分别求出c(x,b)和c(x,b+1):
c(x,b) = c[a+1][b](x-a)+c[a][b](1+a-x);
c(x,b+1) = c[a+1][b+1](x-a)+c[a][b+1](1+a-x);
好,现在已经知道c(x,b)和c(x,b+1)了,而根据假设c(x,b)到c(x,b+1)也是线性变化的,所以:
c(x,y) = c(x,b+1)(y-b)+c(x,b)(1+b-y)

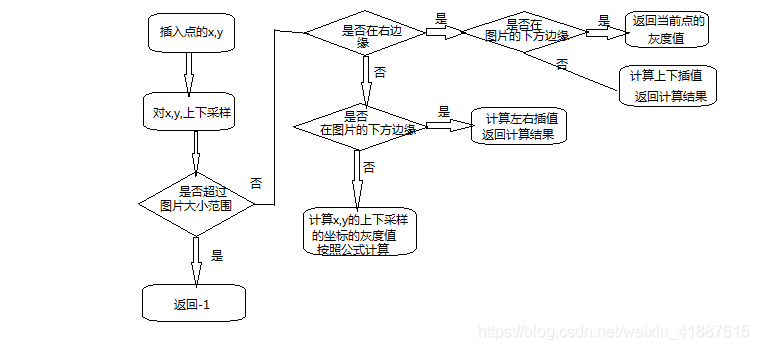
代码:
1 //双线性差值
2 int InterpBilinear(const QImage &image,double x,double y)
3 {
4 int width = image.width();
5 int height = image.height();
6
7 //四个临近点的坐标 (x1,y1)、(x1,y2),(x2,y1),(x2,y2)
8 int x1,x2;
9 int y1,y2;
10
11 //两个差值的中值
12 double f12,f34;
13 double epsilon = 0.0001;
14
15 //四个临近像素坐标x像素值
16 double f1,f2,f3,f4;
17
18 //计算四个临近坐标
19 x1 = (int)x;
20 x2 = x1 + 1;
21 y1 = (int)y;
22 y2 = y1+1;
23
24 //不在图片的范围内
25 if((x < 0) || (x > width - 1) || (y < 0) || (y > height - 1))
26 {
27 return -1;
28 }else{
29 if(fabs(x - width+1)<=epsilon) //如果计算点在右测边缘
30 {
31 //如果差值点在图像的最右下角
32 if(fabs(y - height+1)<=epsilon)
33 {
34 f1 = qGray(image.pixel(x1,y1));
35 return f1;
36 }else {
37 f1 = qGray(image.pixel(x1,y1));
38 f3 = qGray(image.pixel(x1,y2));
39
40 //图像右方的插值
41 return ((int) (f1 + (y-y1)*(f3-f1)));
42 }
43 }
44 //如果插入点在图像的下方
45 else if(fabs(y - height+1)<=epsilon){
46 f1 = qGray(image.pixel(x1,y1));
47 f2 = qGray(image.pixel(x2,y1));
48
49 //图像下方的插值
50 return ((int) (f1 + (x-x1)*(f2-f1)));
51 }
52 else {
53 //得计算四个临近点像素值
54 f1 = qGray(image.pixel(x1,y1));
55 f2 = qGray(image.pixel(x2,y1));
56 f3 = qGray(image.pixel(x1,y2));
57 f4 = qGray(image.pixel(x2,y2));
58
59 //第一次插值
60 f12 = f1 + (x-x1)*(f2-f1); //f(x,0)
61
62 //第二次插值
63 f34 = f3 + (x-x1)*(f4-f3); //f(x,1)
64
65 //最终插值
66 return ((int) (f12 + (y-y1)*(f34-f12)));
67 }
68 }
69 }

