0.PTA得分截图

1.本周学习总结
1.1 总结树及串内容
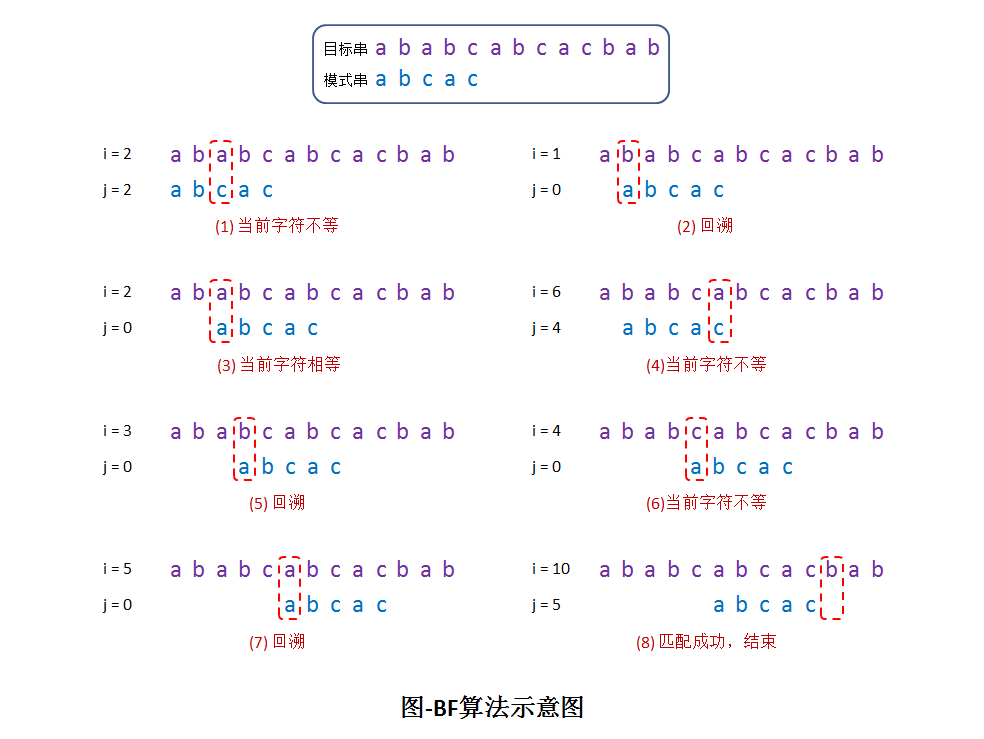
1.串的模式匹配
设有两个串s和t,串t的定位就是要在串s中找到一个与t相等的子串。通常把s称为目标串(target string),把t称为模式串(pattern string),因此串定位查找也称为模式匹配(pattern matching)。模式匹配成功是指在目标串s中找到了一个模式串t;不成功则指目标串s中不存在模式串t。
2.串的BF算法
-
算法背景
- Brute Force(暴力)简称为BF算法,也称简单匹配算法,是一种在字符串匹配的算法中,比较符合人类自然思维方式的方法,即对源字符串和目标字符串逐个字符地进行比较,直到在源字符串中找到完全与目标字符串匹配的子字符串,或者遍历到最后发现找不到能匹配的子字符串。算法思路很简单,但也很暴力。
-
算法思路
- BF算法采用穷举方法,其基本思路是从目标串s的第一个字符开始和模式串t中的第一个字符比较,若相等,则继续逐个比较后续字符;否则从目标串s的第二个字符开始重新与模式串t的第一个字符进行比较。依此类推,若从模式串s的第i个字符开始,每个字符依次和目标串t中的对应字符相等,则匹配成功,该算法返回位置i(表示此时t的第一个字符在s中出现的下标);否则,匹配失败,即t不是s的子串,算法返回-1。
-
算法图示

-
算法代码
int BF(SqString s, SqString t)
{
int i = 0, j = 0;
while (i < s.length && j < t.length) //两个串都没有扫描完时循环
{
if (s.data[i] == t.data[j])//当前比较的两个字符相同
{
i++; j++;//依次比较后续的两个字符
}
else//当前比较的两个字符不相同
{
i = i - j + 1; j = 0;//扫描目标串的i回退,子串从头开始匹配
}
}
if (j >= t.length)//j 超界,表示t是s的子串
return(i - t.length);//返回t在s中的位置
else//模式匹配失败
return(-1);//返回-1
}
- 算法复杂度
- 时间复杂度:假设模式串的长度是m,目标串的长度是n。该算法在最好情况下的时间复杂度为O(m),即主串的前m个字符正好等于模式串的m个字符。在最坏情况下匹配的次数为m(n-m+1),所以其时间复杂度为O(n×m)。其平均时间复杂度也是O(n×m),也就是说,该算法的平均时间性能接近最坏的情况,所以BF算法的效率不高,但容易理解。
- 空间复杂度:不需要额外的存储空间,所以空间复杂度为O(1)。
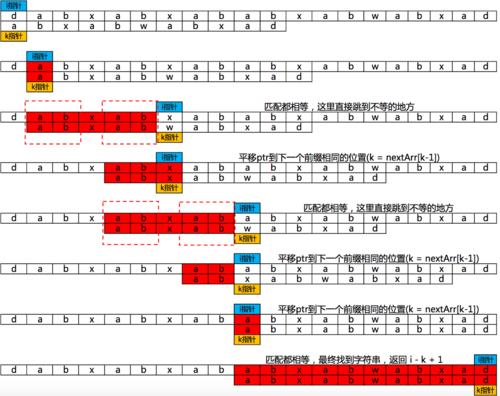
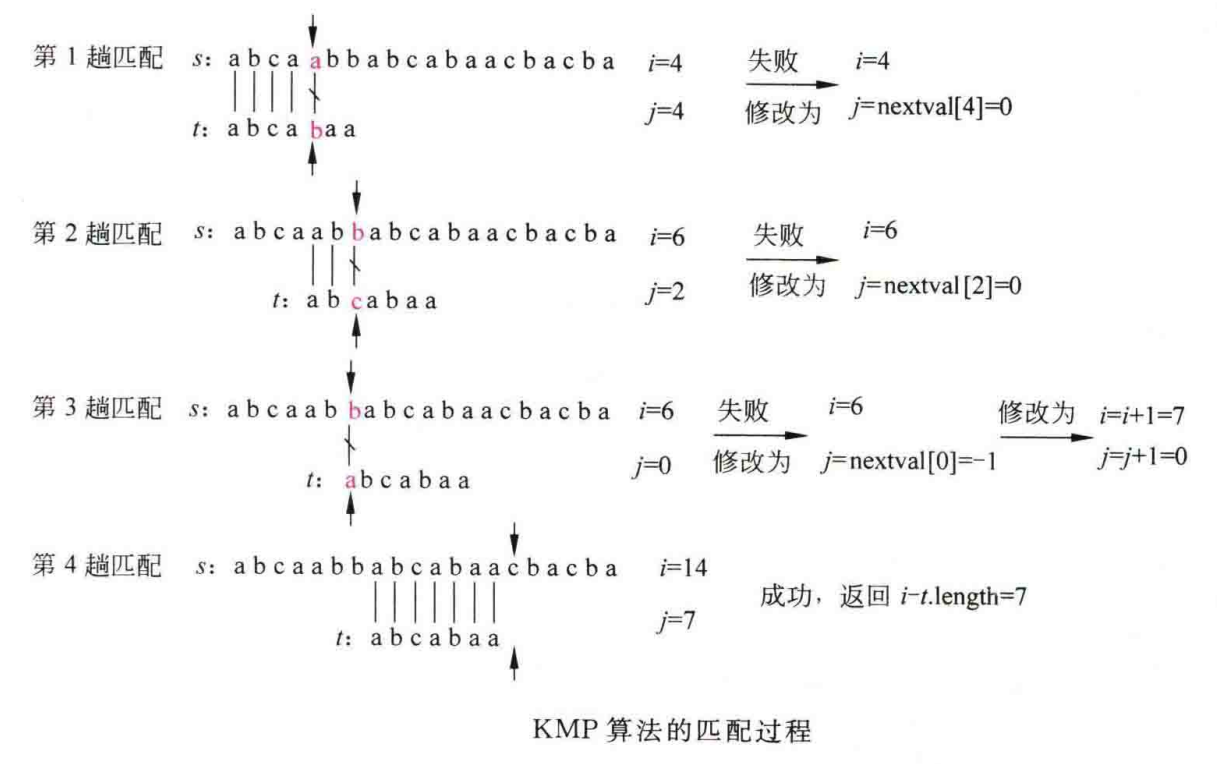
3.串的KMP算法
-
算法背景
- KMP算法是D. E. Knuth、J. H. Morris 和V. R. Pratt共同提出的,称之为Knuth-Morris- Pratt算法,简称KMP算法。该算法与Brute Force算法相比有较大的改进,主要是消除了主串指针的回溯,可以将模式串向右“滑动”尽可能远的一段距离,从而使算法效率有了某种程度的提高。
-
算法思路
- 用 pat 表示模式串,长度为 M,txt 表示文本串,长度为 N。KMP 算法是在 txt 中查找子串 pat,如果存在,返回这个子串的起始索引,否则返回 -1。
- KMP 算法永不回退 txt 的指针 i,不走回头路(不会重复扫描 txt),而是借助 dp 数组中储存的信息把 pat 移到正确的位置继续匹配。
-
算法图示

-
算法代码
//关于next数组的KMP 算法
int KMPIndex(SqString s, SqString t)//KMP 算法
{
int next[MaxSize], i = 0, j = 0;
GetNext(t, next);
while (i < s.length && j < t.length)
{
if (j == -1 || s.data[i] == t.data[j])
{
i++;
j++;//i、j各增1
}
else
{
j = next[i];//i不变, 后退
}
if (j >= t.length)//匹配成功
return(i - t.length);//返回子串位置
else//匹配不成功
return(-1);//返回-1
}
}



//用nextval 取代next,得到改进的KMP算法
void GetNextval(SqString t, int nextval[])//由模式串t求出nextval值
{
int j = 0, k = -1;
nextval[0] = -1;
while (j < t.length)
{
if (k == -1 || t.data[j] == t.data[k])
{
j++; k++;
if (t.data[j] != t.data[k])
nextval[j] = k;
else
nextval[j] = nextval[k];
}
else
k = nextval[k];
}
}
int KMPIndex1(SqString s, SqString t)//改进后的KMP算法
{
int nextval[MaxSize], i = 0, j = 0;
GetNextval(t, nextval);
while (i < s.length && j < t.length)
{
if (j == -1 || s.data[i] == t.data[i])
{
i++;
j++;
}
else
j = nextval[j];
}
if (j >= t.length)
return(i - t.length);
else
return(-1);
}
- 算法复杂度
- 设主串s的长度为n,子串t的长度为m,在KMP算法中求next数组的时间复杂度为O(m),在后面的匹配中因目标串s的下标i不减(即不回溯),比较次数可记为n,所以KMP算法的平均时间复杂度为O(n+m),优于BF算法。但并不等于说任何情况下KMP算法都优于BF算法,当模式串的next数组中next[0]=-1,而其他元素值均为0时,KMP算法退化为BF算法。
- 空间复杂度为O(m),因为需要一个和目标字符串相同长度的备份表
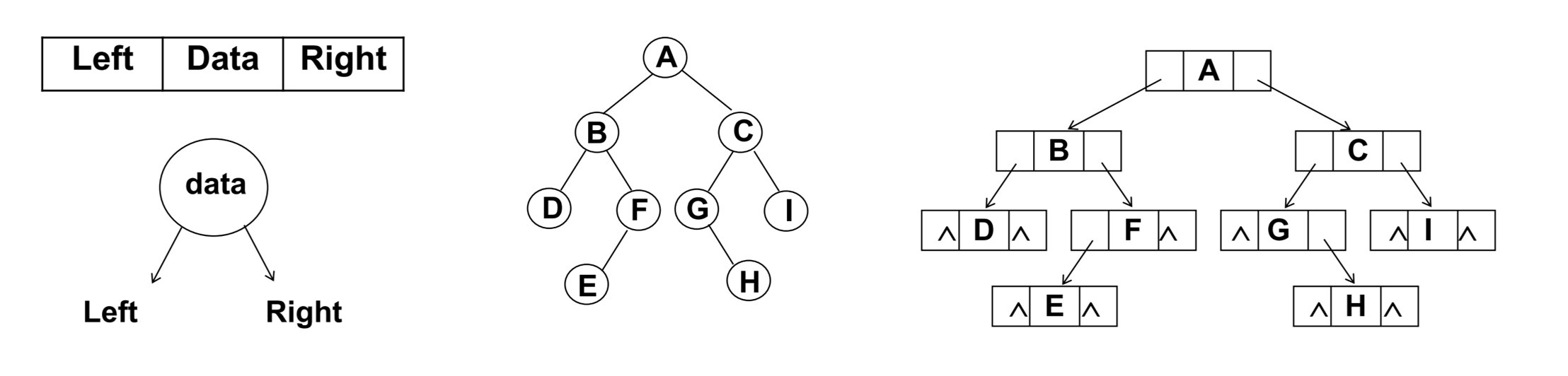
4.树形结构属于非线性结构,常用的树形结构有树和二叉树。线性结构可以表示元素或元素之间的一对一关系,而在树形结构中,一个结点可以与多个结点相对应,因此能够表示层次结构的数据。
5.树
-
树的定义:
- 树(tree)是由n(n≥0)个结点(或元素)组成的有限集合(记为T)。
- 如果n=0,它是一棵空树,这是树的特例。
- 如果n>0,这n个结点中有且仅有一个结点作为树的根结点,简称为根(root),其余结点可分为m(m≥0)个互不相交的有限集T1,T2,...,Tm,其中每个子集本身又是一棵符树,称为根结点的子树(subtree)。
- 所以,从上述可以看出,树的定义是递归的,因为在树的定义中又用到树定义。它刻化了树的固有特性,即一棵树由若干棵互不相交的子树构成,而子树又由更小的若干棵子树构成。
-
树的术语:
- 根——即根结点(没有前驱)
- 叶子——即终端结点(没有后继)
- 森林——指m棵不相交的树的集合
- 有序树——结点各子树从左至右有序,不能互换(左为第一)
- 无序树——结点各子树可互换位置
- 双亲——即上层的那个结点(直接前驱)
- 孩子——即下层结点的子树的根(直接后继)
- 兄弟——同一双亲下的同层结点(孩子之间互称兄弟)
- 祖先——即从根到该结点所经分支的所有结点
- 子孙——即该结点下层子树中的任一结点
- 结点——即树的数据元素
- 结点的度——结点挂接的子树数,分支数目
- 树的度——树中所有结点的度中的最大值,通常将度为m的树称m次树
- 结点的层次——从根到该结点的层数(根结点算第一层)
- 终端结点——即度为0的结点,即叶子
- 分支结点——即度不为0的结点(也称为内部结点)
- 树的深度或高度——指所有结点中最大的层数
-
树的性质:
- 性质1:树中的结点数等于所有结点的度数之和加1
- 性质2:度为m的树中第i层上至多有m^(i-1)个结点(i≥1)
- 性质3:高度为h的m次树最多有(m^h-1)/(m-1)个结点
- 性质4:具有n个结点的m次树的最小高度为┌logm (n(m- 1)+1)┐
-
eg:
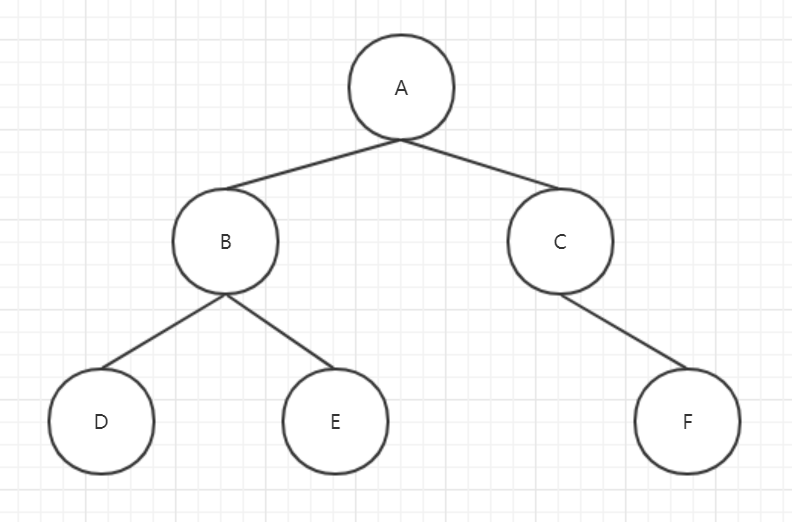
- 性质1:树中的结点数为6,所有结点的度数之和为2+2+1+0+0+0=5
- 性质2:该树的度为2,第2层上至多有2^(2-1) = 2个结点,第3层上至多有2^(3-1) = 4个结点
- 性质3:该树的高度为3,度为2,为2次树,最多有(2^3-1)/(2-1)= 7个结点
-
树的基本运算,主要分为以下3大类:
- 寻找满足某种特定条件的结点,如寻找当前结点的双亲结点等
- 插入或删除某个结点,如在树的指定结点上插入一个孩子结点或删除指定结点的第i个孩子结点等
- 遍历树中的所有结点
-
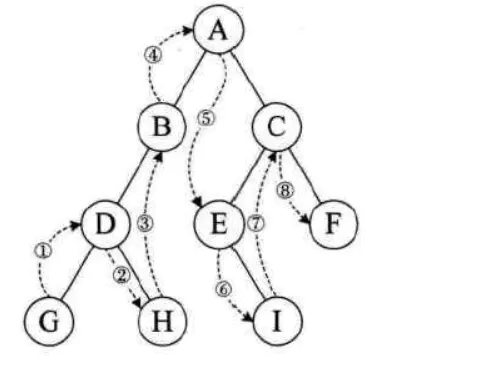
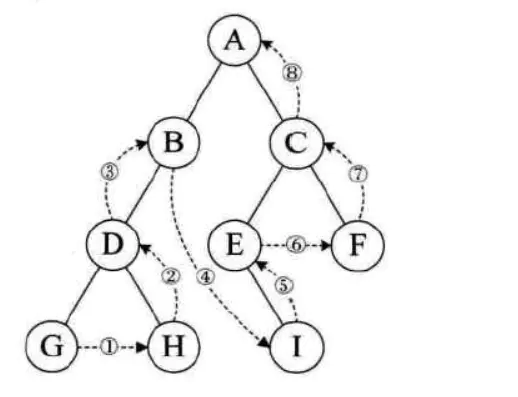
树的遍历
- 树的遍历运算是指按某种方式访问树中的所有结点且每一个结点只被访问一次。树的遍历方式主要有先根遍历、后根遍历和层次遍历3种。注意,树的先根遍历和后根遍历过程都是递归的。
★ 先序遍历:若树不空,则先访问根结点,然后依次先根遍历左右子树。【根左右】
void PreOrder(BTree bt)
{
if (bt!=NULL)
{ cout << bt->data;//访问根结点
PreOrder(bt->lchild);
PreOrder(bt->rchild);
}
}
★ 中序遍历:若树不空,则先遍历左子树,然后访问根结点,最后遍历右子树。【左根右】
void InOrder(BTree bt)
{
if (bt!=NULL)
{ InOrder(bt->lchild);
cout << bt->data;//访问根结点
InOrder(bt->rchild);
}
}
★后序遍历:若树不空,则先依次后根遍历各棵子树,然后访问根结点。【左右根】
void PostOrder(BTree bt)
{
if (bt!=NULL)
{ PostOrder(bt->lchild);
PostOrder(bt->rchild);
cout << bt->data;//访问根结点
}
}
★层次遍历:若树不空,则自上而下、自左至右访问树中每个结点。
void PrintTree(BTree BT)//层次遍历
{
BTree bt;
int flag = 0;//flag表示该结点的次序
queue<BTree>qu;
qu.push(BT);//将树入队
while (!qu.empty())//遍历队列
{
bt = qu.front();//将结点赋给bt
qu.pop();//队首元素出队
if (flag != 0)//如果flag不是0,说明不是第一个,前面输出一个空格,所以也就是说,第一个数据不含空格的输出,空格和其后面的数据绑定
{
cout << " ";
}
cout << bt->data;//输出数据
if (bt->lchild != NULL)//如果bt结点的左右孩子不为空,将其孩子入队
{
qu.push(bt->lchild);
}
if (bt->rchild != NULL)
{
qu.push(bt->rchild);
}
flag++;
}
}
-
eg:

- 先序遍历:A B C D E F G H I
- 中序遍历:B D C A E H G I F
- 后序遍历:D C B H I G F E A
- 层次遍历:A B E C F D G H I
-
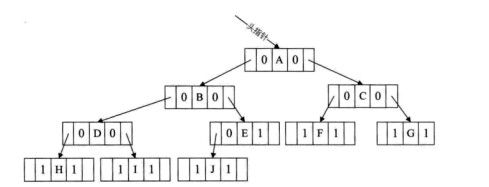
树的存储结构
一)双亲存储结构
①介绍
以双亲作为索引的关键词的一种存储方式
每个结点只有一个双亲,所以选择顺序存储占主要
以一组连续空间存储树的结点,同时在每个结点中,附设一个指示其双亲结点位置的指针域
②结点结构体定义

typedef struct
{ ElemType data; //结点的值
int parent; //指向双亲的位置
} PTree[MaxSize];

③优缺点
优点:parent指针域指向数组下标,所以找双亲结点的时间复杂度为O(1),找双亲结点容易
缺点:由上向下找就十分慢,若要找结点的孩子或者兄弟,要遍历整个树,找孩子很不容易
二)孩子链存储结构
①介绍
由于每个结点可有多个子树(无法确定子树个数),可以考虑使用多重链表来实现,根据树的度来设置孩子域的个数
②结点结构体定义

typedef struct node
{ ElemType data; //结点的值
struct node *sons[MaxSons]; //指向孩子结点
} TSonNode;
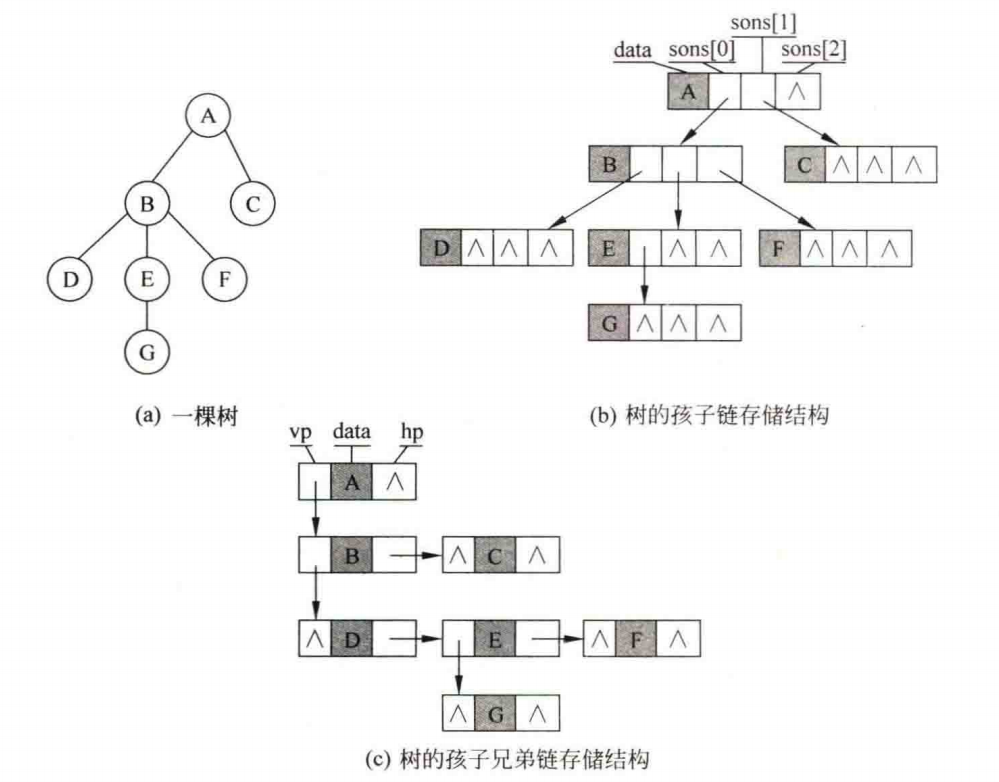
③优缺点
优点:找孩子容易
缺点:空指针太多,找父亲不容易
三)孩子兄弟链存储结构
①介绍
任意一棵树,它的结点的第一个孩子如果存在就是唯一的,它的右兄弟存在也是唯一的。因此,设置两个指针,分别指向该结点的第一个孩子和此结点的右兄弟
②结点结构体定义
typedef struct tnode
{ ElemType data; //结点的值
struct tnode *son; //指向兄弟
struct tnode *brother; //指向孩子结点
} TSBNode;
③优缺点
优点:找第一个孩子和右一个兄弟容易
缺点:每个结点固定只有两个指针域,类似二叉树,找父亲不容易
ps:在一棵树T中最常用的操作是查找某个结点的祖先结点时,采用双亲存储结构最合适;查找某个结点的所有兄弟时,采用孩子链存储结构或者孩子兄弟链存储结构最合适
6.二叉树
1>二叉树的定义
- 二叉树是一个有限的结点集合,这个集合或者为空,或者由一个根结点和两棵互不相交的称为左子树和右子树的二叉树组成。
2>二叉树的五种基本形态
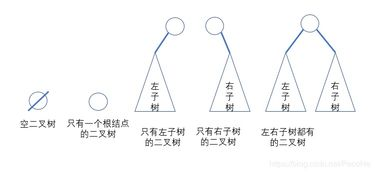
3>二叉树的特点:
(1)每个结点最多有两棵子树
(2)左子树和右子树是有顺序的
(3)即使树中某结点只有一棵子树,也要区分左右

4>两种特殊的二叉树:
-
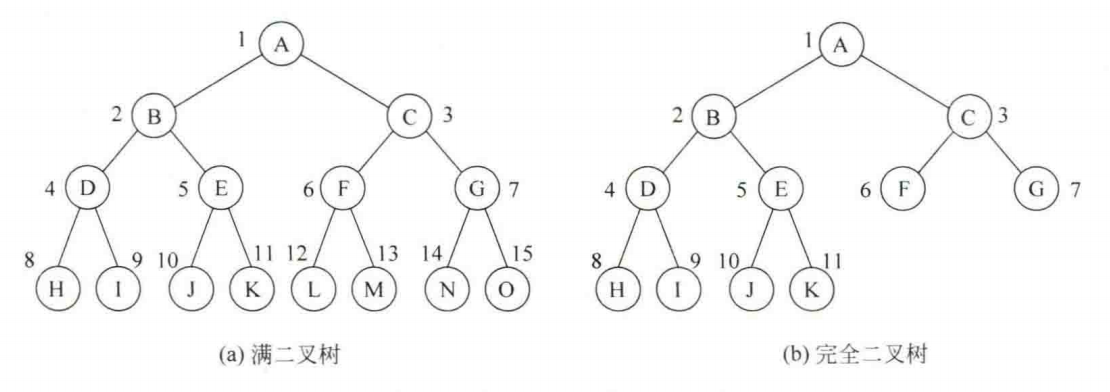
满二叉树:
- 在一棵二叉树中,如果所有分支结点都有双分结点,并且叶结点都集中在二叉树的最下一层,那么这样的二叉树就可称为满二叉树
- 高度为h的满二叉树恰好有 2^h-1 个结点
-
完全二叉树:
- 若二叉树中最多只有最下面两层的结点的度数可以小于2,并且最下面一层的叶子结点都依次排列在该层最左边的位置上,则这样的二叉树称为完全二叉树
- 换句话说,满二叉树是完全二叉树的一种特例,满二叉树是叶子一个也不少的树,而完全二叉树虽然前n-1层是满的,但最底层却允许在右边缺少连续若干个结点,并且完全二叉树与同高度的满二叉树的对应位置结点有同一编号,完全二叉树实际上是对应的满二叉树删除叶结点层最右边若干个结点得到的
- 完全二叉树的性质:
●叶子结点只可能在最下面两层中出现
●对于最大层次中的叶子结点,都依次排列在该层最左边的位置上
●如果有度为1的结点,只可能有一个,且该结点只有左孩子而无右孩子
●按层序编号时,一旦出现编号为i的结点是叶子结点或只有左孩子,则编号大于i的结点均为叶子结点
●n1可由n的奇偶性确定,当结点总数n为奇数时,n1=0,当结点总数n为偶数时,n1=1
●除树根结点外,若一个结点的编号为i,则它的双亲结点的编号为└i/2┘
●若编号为i的结点有左孩子结点,则左孩子结点的编号为2i;若编号为i的结点有右孩子结点,则右孩子结点的编号为2i+1
●若i≤└n/2┘,则编号为i的结点为分支结点,否则为叶结点
5>二叉树的性质:
- 非空二叉树上叶节点数等于双分支节点数加1,即n0=n2+1
- 在二叉树的第 i 层上至多有 2^(i-1) 个结点 (i≥1)
- 高度为h的二叉树至多有2^h-1个节点(h≥1)
- 具有n个结点的完全二叉树的深度必为 └log2n┘ + 1
6>二叉树存储结构:
①二叉树的顺序存储结构
- 二叉树的顺序存储结构是指用一组地址连续的存储单元依次自上而下、自左至右存储完全二叉树上的结点元素,即将完全二叉树上编号为i的结点元素存储在某个数组下标为i-1的分量中,然后通过一些方法确定结点在逻辑上的父子和兄弟关系。
- 完全二叉树和满二叉树采用顺序存储比较合适,节省空间且数组元素下标值能确定结点在二叉树中的位置和结点之间的关系。但对于一般二叉树,则需要添加一些并不存在的空结点,所以效率并不高。
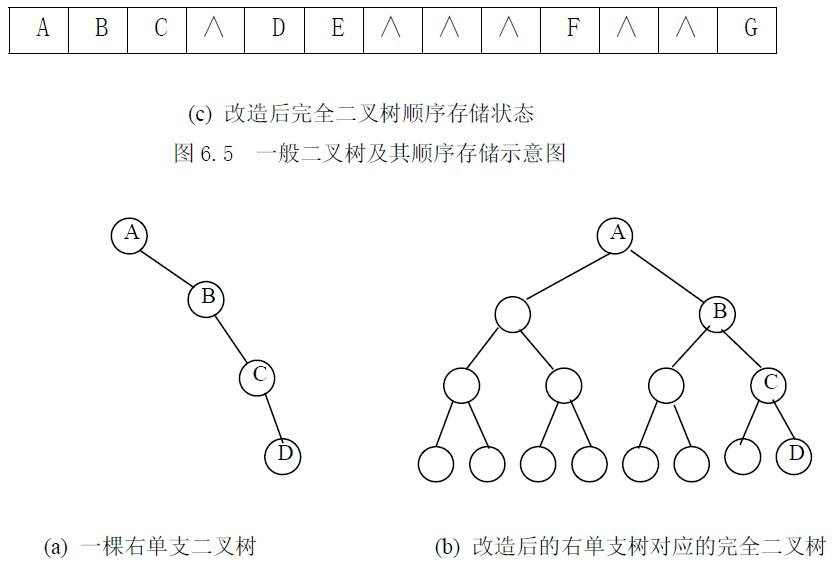
typedef struct
{
int data[MAXSIZE]; //存放二叉树的节点值
int n;//元素个数
}BTree;
- 这种存储结构显然要从数组下标1开始存储树中的结点。同时也要注意区别树的顺序存储结构与二叉树的顺序存储结构。在树的顺序存储结构中,数组下标代表结点的编号,下标上所存的内容指示了结点之间的关系。而在二叉树的顺序存储结构中,数组下标既代表了结点的编号,又指示了树中各结点之间的关系。二叉树属于树,因此二叉树都可以用树的存储结构来存储,但树却不能都用二叉树的存储结构来存储。
- 二叉树顺序存储结构缺点:对于完全二叉树来说,其顺序存储是十分合适的。在最坏的情况下,一个深度为k且只有k个结点的单支树(树中不存在度为2的结点)却需要2k-1的一维数组。空间利用率太低,数组,查找、插入删除不方便。
②二叉树的链式存储结构
- 顺序存储的空间利用率比较低,所以二叉树一般都采用链式存储结构。链式结构是指用一个链表来存储一棵二叉树,二叉树中的每个结点用链表的一个链结点来存储。
- 在二叉树中,结点结构通常包括若干数据域和若干指针域。二叉链表至少包含3个域:数据域data、左指针域lchild和右指针域rchild。

typedef struct node
{
int data;//数据元素
struct node *lchild;//指向左孩子
struct node *rchild;//指向右孩子
}BTree;
- 在含有n个结点的二叉链表中,含有2n个指针域,其中有n+1个空链域,n-1个非空指针域。
7>二叉树的基本运算及其实现
- 二叉树的创建
★顺序创建二叉树
BTree Creat(BTree &bt,char str[], int i)
{
BTree bt;
if (i > strlen(str))
return NULL;
if (str[i] == '#')
return NULL;
bt = new Node;
bt->data = str[i];
bt->lchild = Creat(bt,str, 2*i);
bt->rchild = Creat(bt,str, 2*i+1);
return bt;
}
★链式创建二叉树
BTree Creat(char str[], int &i)
{
BTree bt;
if (i > strlen(str))
return NULL;
if (str[i] == '#')
return NULL;
bt = new Node;
bt->data = str[i];
bt->lchild = Creat(str, ++i);
bt->rchild = Creat(str, ++i);
return bt;
}
- 二叉树的遍历
- 二叉树的遍历是指按照一定次序访问树中所有节点,并且每个节点仅被访问一次的过程。它是最基本的运算,是二叉树中所有其他运算的基础。
★先序遍历二叉树
//先序遍历二叉树的过程是:访问根节点;先序遍历左子树;先序遍历右子树。
void PreOrderTraverse(BiTree T)
{
if(T!=NULL)
{
printf("%c",T->data);
PreOrderTraverse(T->lchild);
PreOrderTraverse(T->rchild);
}
}

★中序遍历二叉树
//中序遍历二叉树的过程是:中序遍历左子树;访问根节点;中序遍历右子树。
void InOrderTraverse(BiTree T)
{
if(T!=NULL)
{
PreOrderTraverse(T->lchild);
printf("%c",T->data);
PreOrderTraverse(T->rchild);
}
}
★后序遍历二叉树
//后序遍历二叉树的过程是:后序遍历左子树;后序遍历右子树;访问根节点。
void PostOrderTraverse(BiTree T)
{
if(T!=NULL)
{
PreOrderTraverse(T->lchild);
PreOrderTraverse(T->rchild);
printf("%c",T->data);
}
}
★层次遍历二叉树
//在进行层次遍历时,对某一层的节点访问完后,再按照它们的访问次序对各个节点的左、右孩子顺序访问。
void LayerOrder(BTreeNode *t)
{
queue<BTreeNode*> q;
BTreeNode *temp;
if(t == NULL) return;
q.push(t);
while(!q.empty())
{
temp = q.front();
q.pop();
cout<<temp->data<<' ';
if(temp->lchild != NULL)
q.push(temp->lchild);
if(temp->rchild != NULL)
q.push(temp->rchild);
}
}
层次遍历过程是:
初始化队列,先将根节点进队。
while(队列不空)
{ 队列中出列一个节点*p,访问它;
若它有左孩子节点,将左孩子节点进队;
若它有右孩子,将右孩子进队。
}
- 二叉树的销毁
void DestroyBTree(BTree bt)
{
if (bt != NULL)
{
DestroyBTree(bt->lchild);
DestroyBTree(bt->rchild);
delete bt;
}
}
8>二叉树的应用
#include<cstring>
#include<cstdio>
#include<iostream>
using namespace std;
typedef struct treepoint* tNode;
typedef struct queue* qNode;
typedef struct stack* sNode;
struct treepoint {
char date;
tNode lson, rson;
};
char s[110];
int pos;
tNode build() {//建立二叉树
tNode bt = (tNode)malloc(sizeof(treepoint));
pos++;
if (s[pos] == '#')bt = NULL;
else {
bt->date = s[pos];
bt->lson = build();
bt->rson = build();
}
return bt;
}
void pre_order_travel(tNode bt) {//前序遍历
printf("%c", bt->date);
if (bt->lson != NULL)
pre_order_travel(bt->lson);
if (bt->rson != NULL)
pre_order_travel(bt->rson);
//free(bt);
}
void mid_order_travel(tNode bt) {//中序遍历
if (bt->lson != NULL)
mid_order_travel(bt->lson);
printf("%c", bt->date);
if (bt->rson != NULL)
mid_order_travel(bt->rson);
//free(bt);
}
void post_order_travel(tNode bt) {//后序遍历
if (bt->lson != NULL)
post_order_travel(bt->lson);
if (bt->rson != NULL)
post_order_travel(bt->rson);
printf("%c", bt->date);
//free(bt);
}
struct stack {
tNode value;
sNode next;
};
sNode top;
void Stack_creat() {
top = (sNode)malloc(sizeof(stack));
top->next = NULL;
}
void Stack_push(tNode item) {
sNode temp = (sNode)malloc(sizeof(stack));
temp->next = top->next;
temp->value = item;
top->next = temp;
}
bool Stack_empty() {
return top->next == NULL;
}
void Stack_pop() {
sNode temp = top->next;
top->next = temp->next;
}
void iter_Inorder(tNode root) {//非递归遍历二叉树
Stack_creat();
if (root != NULL) {
Stack_push(root);
}
while (!Stack_empty()) {
sNode temp = top->next;
cout << temp->value->date;
Stack_pop();
if (temp->value->rson) {
Stack_push(temp->value->rson);
}
if (temp->value->lson) {
Stack_push(temp->value->lson);
}
}
cout << endl;
}
qNode front, rear;
struct queue {
tNode value;
qNode next;
};
void Queue_creat() {
front = (qNode)malloc(sizeof(queue));
rear = (qNode)malloc(sizeof(queue));
front->next = rear;
}
bool Queue_empty() {
return front->next == rear;
}
void Queue_delete() {
qNode temp = front->next;
front->next = temp->next;
}
void Queue_push(tNode item) {
qNode temp = (qNode)malloc(sizeof(queue));
rear->value = item;
rear->next = temp;
temp->next = NULL;
rear = temp;
}
void level_order(tNode root) {//二叉树的层序遍历
if (root == NULL) {
cout << endl;
}
Queue_creat();
Queue_push(root);
while (!Queue_empty()) {
qNode temp = front->next;
Queue_delete();
cout << temp->value->date;
if (temp->value->lson != NULL) {
Queue_push(temp->value->lson);
}
if (temp->value->rson != NULL) {
Queue_push(temp->value->rson);
}
}
cout << endl;
}
int leaf(tNode bt) {//计算叶子节点数量
int flag = 0;
int cnt = 0;
if (bt->lson != NULL)
cnt += leaf(bt->lson);
else
flag++;
if (bt->rson != NULL)
cnt += leaf(bt->rson);
else
flag++;
if (flag == 2)
cnt = 1;
return cnt;
}
int maxheight = 0;
void height(tNode bt, int now) {//计算树的深度
if (now > maxheight)maxheight = now;
if (bt->lson != NULL)
height(bt->lson, now + 1);
if (bt->rson != NULL)
height(bt->rson, now + 1);
}
int main() {
while (~scanf("%s", s + 1)) {//输入二叉树的前序遍历来建树
pos = 0;
tNode root = build();
cout << "先序遍历: ";
pre_order_travel(root); cout << endl;
cout << "中序遍历: ";
mid_order_travel(root); cout << endl;
cout << "后序遍历: ";
post_order_travel(root); cout << endl;
cout << "二叉树的非递归遍历: ";
iter_Inorder(root);
cout << "二叉树的层序遍历: ";
level_order(root);
printf("叶子结点数: %d\n", leaf(root));
maxheight = 0;
height(root, 1);
printf("树的深度为: %d\n", maxheight);
}
}
★二叉树的应用有表达式树、目录树、哈夫曼树等等
★表达式树
1.树中叶子结点均为操作数,分支结点均为运算符。
2.运算符栈
3.存放树根栈
while(遍历表达式)
{
若为操作数,生成树结点,入树根栈
若为运算符:
若优先级>栈顶运算符,则入运算符栈
若小于,出栈,树根栈弹出2个结点建树,新生成树根入树根栈
若相等,则出栈栈顶运算符
}

7.线索二叉树
- 二叉链存储结构时,每个节点有两个指针域,总共有2n个指针域。有效指针域:n-1(根节点没指针指向),空指针域:n+1。利用这些空链域,指向该线性序列中的“前驱”和“后继”的指针,称作线索。
- 若结点有左子树,则lchild指向其左孩子;否则, lchild指向其直接前驱(即线索);
- 若结点有右子树,则rchild指向其右孩子;否则, rchild指向其直接后继(即线索) 。
- 在决定lchild是指向左孩子还是前驱,rchild是指向右孩子还是后继,需要一个区分标志的。因此,我们在每个结点再增设两个标志域ltag和rtag,注意ltag和rtag只是区分0或1数字的bool型变量,其占用内存空间要小于像lchild和rchild的指针变量。结点结构如下所示。

- ltag为0时指向该结点的左孩子,为1时指向该结点的前驱;rtag为0时指向该结点的右孩子,为1时指向该结点的后继;
typedef struct node
{ ElemType data; //结点数据域
int ltag,rtag; //增加的线索标记
struct node *lchild; //左孩子或线索指针
struct node *rchild; //右孩子或线索指针
} TBTNode; //线索树结点类型定义
-
优缺点:
- 优势:
(1)利用线索二叉树进行中序遍历时,不必采用堆栈处理,速度较一般二叉树的遍历速度快,且节约存储空间。
(2)任意一个结点都能直接找到它的前驱和后继结点。 - 劣势:
(1)结点的插入和删除麻烦,且速度也较慢。
(2)线索子树不能共用。
- 优势:
-
中序遍历线索二叉树
voidInThreading(BiThrTree* p)/*通过中序遍历进行中序线索化*/
{
if (p)
{
InThreading(p->lchild);/*左子树线索化,递归*/
if (p->lchild == NULL)/*前驱线索*/
{
p->ltag = 1;
p->lchild = pre;
}
else
p->ltag = 0;
if (p->rchild == NULL)
p->rtag = 1;/*后驱线索*/
else
p->rtag = 0;
if (pre != NULL && pre->rtag == 1)
pre->rchild = p;
pre = p;
InThreading(p->rchild);/*右子树线索化*/
}
}
- 求前驱的算法如下:
bithptr* INORDERNEXT(bithptr* p)
{
if (p->ltag == 1)
return(p->lchild);
else
{
q = p->lchild;/*找左子树最后访问的结点*/
while (q->rtag == 0)
q = q->rchild;
return(q);
}
}
- 求后继的算法如下:
bithptr* INORDERNEXT(bithptr* p)
{
if (p->rtag == 1)
return(p->rchild);
else
{
q = p->rchild;/*找右子树最先访问的结点*/
while (q->ltag == 0)
q = q->lchild;
return(q);
}
}
- 双向线索二叉树
- 实现过程:在线索二叉树的基础上,额外添加一个结点。此结点的作用类似于链表中的头指针,数据域不起作用,只利用两个指针域(由于都是指针,标志域都为 0 )。左指针域指向二叉树的树根,确保可以正方向对二叉树进行遍历;同时,右指针指向线索二叉树形成的线性序列中的最后一个结点。这样,二叉树中的线索链表就变成了双向线索链表,既可以从第一个结点通过不断地找后继结点进行遍历,也可以从最后一个结点通过不断找前趋结点进行遍历。
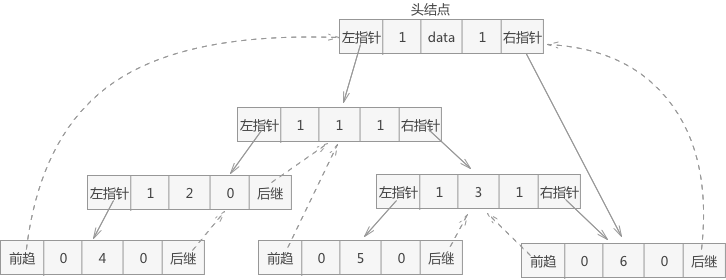
- 实现过程:在线索二叉树的基础上,额外添加一个结点。此结点的作用类似于链表中的头指针,数据域不起作用,只利用两个指针域(由于都是指针,标志域都为 0 )。左指针域指向二叉树的树根,确保可以正方向对二叉树进行遍历;同时,右指针指向线索二叉树形成的线性序列中的最后一个结点。这样,二叉树中的线索链表就变成了双向线索链表,既可以从第一个结点通过不断地找后继结点进行遍历,也可以从最后一个结点通过不断找前趋结点进行遍历。
//建立双向线索链表
void InOrderThread_Head(BiThrTree *h, BiThrTree t)
{
//初始化头结点
(*h) = (BiThrTree)malloc(sizeof(BiThrNode));
if((*h) == NULL){
printf("申请内存失败");
return ;
}
(*h)->rchild = *h;
(*h)->Rtag = Link;
//如果树本身是空树
if(!t){
(*h)->lchild = *h;
(*h)->Ltag = Link;
}
else{
pre = *h;//pre指向头结点
(*h)->lchild = t;//头结点左孩子设为树根结点
(*h)->Ltag = Link;
InThreading(t);//线索化二叉树,pre结点作为全局变量,线索化结束后,pre结点指向中序序列中最后一个结点
pre->rchild = *h;
pre->Rtag = Thread;
(*h)->rchild = pre;
}
}
- [双向线索二叉树的建立及实现] (http://data.biancheng.net/view/29.html)
8.哈夫曼树
-
含义:设二叉树具有n个带权值的叶子节点,那么从根节点到各个叶子节点的路径长度与相应节点权值的乘积的和,叫做二叉树的带权路径长度。
而具有最小带权路径长度的二叉树称为哈夫曼树。哈夫曼树又称最优二叉树,是一种带权路径长度最短的二叉树。所谓树的带权路径长度,就是树中所有的叶结点的权值乘上其到根结点的路径长度(若根结点为0层,叶结点到根结点的路径长度为叶结点的层数)。树的路径长度是从树根到每一结点的路径长度之和,记为WPL=(W1L1+W2L2+W3L3+...+WnLn),N个权值Wi(i=1,2,...n)构成一棵有N个叶结点的二叉树,相应的叶结点的路径长度为Li(i=1,2,...n)。可以证明哈夫曼树的WPL是最小的。

-
构造原理:
- 权值越大的叶结点越靠近根结点。
- 权值越小的叶结点越远离根结点。

-
结点结构体定义:
typedef struct {
char data;//结点值
double weight;//权重
int parent;//双亲结点
int lchild;//左孩子结点
int rchild;//右孩子结点
} HTNode;
-
相关概念:
- 路径:在一棵树中,一个结点到另一个结点之间的通路。
- 路径长度:在一条路径中,每经过一个结点,路径长度都要加 1 。例如在一棵树中,规定根结点所在层数为1层,那么从根结点到第 i 层结点的路径长度为 i - 1 。
- 结点的权:给每一个结点赋予一个新的数值,被称为这个结点的权。
- 结点的带权路径长度:指的是从根结点到该结点之间的路径长度与该结点的权的乘积。
- 树的带权路径长度(WPL):树中所有叶子结点的带权路径长度之和。
-
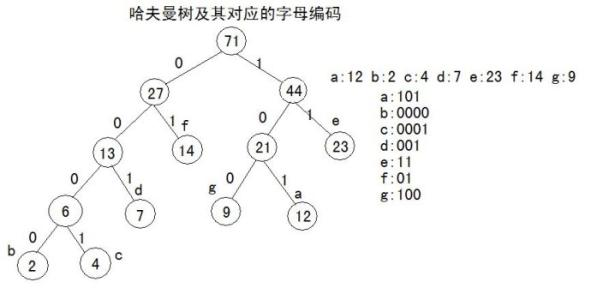
哈夫曼树的构造
假设有n个权值,则构造出的哈夫曼树有n个叶子结点。 n个权值分别设为 w1、w2、…、wn,则哈夫曼树的构造规则为:- (1) 将w1、w2、…,wn看成是有n 棵树的森林(每棵树仅有一个结点);
- (2) 在森林中选出两个根结点的权值最小的树合并,作为一棵新树的左、右子树,且新树的根结点权值为其左、右子树根结点权值之和;
- (3)从森林中删除选取的两棵树,并将新树加入森林;
- (4)重复(2)、(3)步,直到森林中只剩一棵树为止,该树即为所求得的哈夫曼树。
-
给哈夫曼树所有的左分支加上0,给所有的右分支加上1,从而得到各字母的哈夫曼编码。
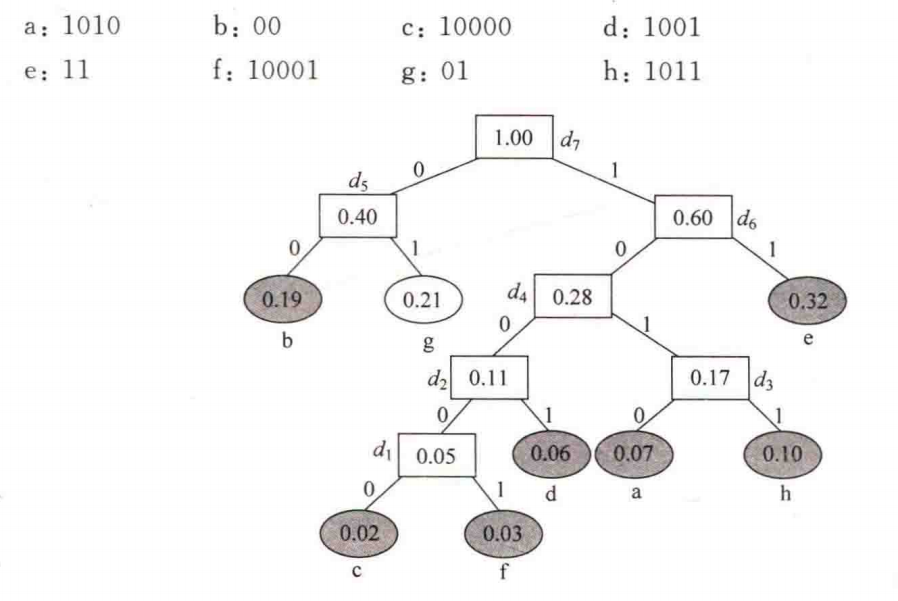
ps:该棵哈夫曼树的带权路径长度WPL=4×0.07+2×0.19+5×0.02+4×0.06+2×0.32+5×0.03+2×0.21+4×0.1=2.61
9.并查集
- 概念:并查集支持查找一个元素所属的集合以及两个元素各自所属的集合的合并等运算。当给出两个元素的一个无序对(a,b)时,需要快速“合并”a和b分别所在的集合,这期间需要反复“查找"某元素所在的集合。“并”、“查”和“集"3个字由此而来。在这种数据类型中,n个不同的元素被分为若干组。每组是一个集合,这种集合叫分离集合,称之为并查集。
- 在并查集中,每个分离集合对应的一棵树,称为分离集合树。整个并查集也就是一棵分离集合森林。
- 应用:比如朋友圈、亲戚朋友等等。
- 并查集的基本操作:
- makeSet(s):建立一个新的并查集,其中包含 s 个单元素集合。
- unionSet(x, y):把元素 x 和元素 y 所在的集合合并,要求 x 和 y 所在的集合不相交,如果相交则不合并。
- find(x):找到元素 x 所在的集合的代表,该操作也可以用于判断两个元素是否位于同一个集合,只要将它们各自的代表比较一下就可以了。
- 并查集的实现原理也比较简单,就是使用树来表示集合,树的每个节点就表示集合中的一个元素,树根对应的元素就是该集合的代表。
- 初始化并查集树
void MAKE SET(UFSTree t[], int n)//初始化并查集树
{
int i;
for (i = 1; i <= n; i++)
{
t[i].data = i;//数据为该人的编号
t[i].rank = 0;//秩初始化为0
t[i].parent = i;//双亲初始化指向自己
}
}
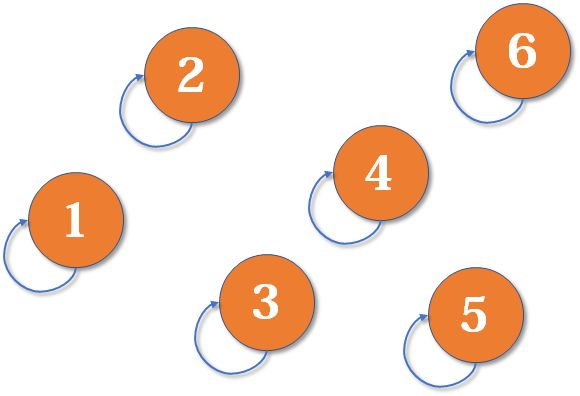
- 查找一个元素所属的集合
int FIND_ SET(UFSTree t[], int x)//在x所在的子树中查找集合编号
{
if (x != t[x].parent)//双亲不是自己
return(FIND_ SET(t, t[x].parent));//递归在双亲中找x
else
return(x);//双亲是自己,返回x
}

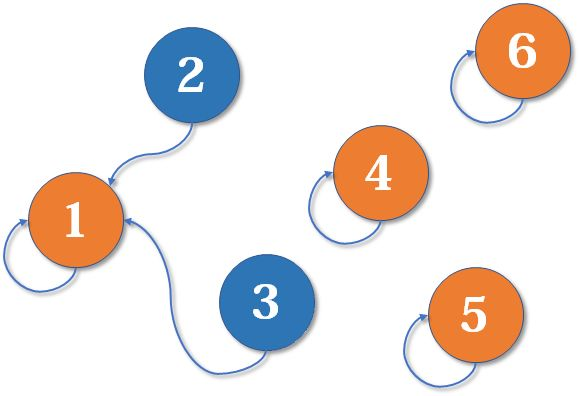

- 两个元素各自所属的集合的合并
void UNION(UFSTree t[], int x, int y)//将x和y所在的子树合并
{
x = FIND SET(t, x);//查找x所在分离集合树的编号
y = FIND SET(t, y);//查找y所在分离集合树的编号
if (t[x].rank > t[y].rank)//y结点的秩小于x结点的秩
t[y].parent = x;//将y连到x结点上,x作为y的双亲结点
else//y结点的秩大于等于x结点的秩
{
t[x].parent = y;//将x连到y结点上,y作为x的双亲结点
if (t[x].rank == t[y].rank)//x和y结点的秩相同
t[y].rank++;//y结点的秩增1
}
}
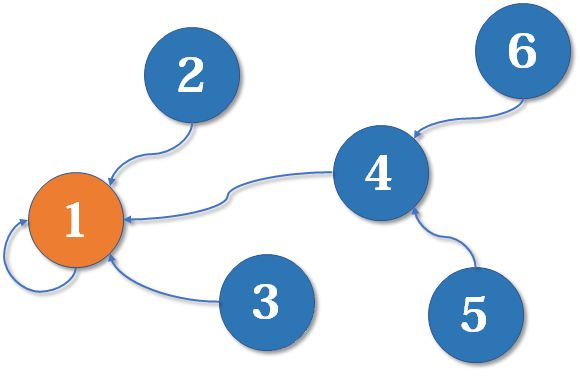
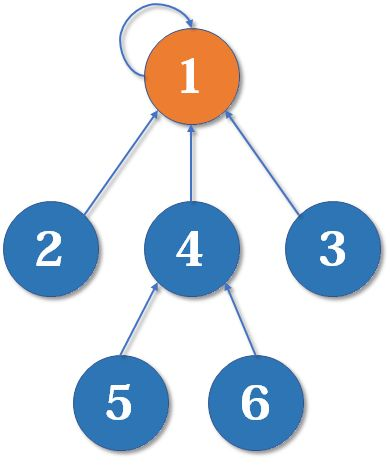
- 对于n个人,本算法的时间复杂度为O(log2n)。
1.2 谈谈你对树的认识及学习体会
- 树这一部分的内容感觉比以前更麻烦,因为就建树来说就有很多种不同的表示方法,可以层次遍历,可以前序、中序和后序等等,其中往往还夹杂着不好理解的函数的递归调用,感觉比较绕
- 往往这一部分的题目是你不容易写出来代码,但是当你去看例子时,却感觉原来如此,恍然大悟的样子,但是绕来绕去自己不清楚
- 不过这部分的题如果自己去推算一些填空选择题的话,通过画画图的方法还是容易做出来的,但是写代码就不太好了o(╥﹏╥)o
2.阅读代码
2.1 树的子结构
- 题目
输入两棵二叉树A和B,判断B是不是A的子结构。(约定空树不是任意一个树的子结构)
B是A的子结构, 即 A中有出现和B相同的结构和节点值。
例如:
给定的树 A:
3
/ \
4 5
/ \
1 2
给定的树 B:
4
/
1
返回 true,因为 B 与 A 的一个子树拥有相同的结构和节点值。
示例 1:
输入:A = [1,2,3], B = [3,1]
输出:false
示例 2:
输入:A = [3,4,5,1,2], B = [4,1]
输出:true
限制:
0 <= 节点个数 <= 10000
- 代码
class Solution {
public:
bool helper(TreeNode* A, TreeNode* B) {
if (A == NULL || B == NULL) {
return B == NULL ? true : false;
}
if (A->val != B->val) {
return false;
}
return helper(A->left, B->left) && helper(A->right, B->right);
}
bool isSubStructure(TreeNode* A, TreeNode* B) {
if (A == NULL || B == NULL) {
return false;
}
return helper(A, B) || isSubStructure(A->left, B) || isSubStructure(A->right, B);
}
};
2.1.1 该题的设计思路
-
取母树为 A ,子树为 B ,若树 B 是树 A 的子结构,则子结构的根节点可能为树 A 的任意一个节点,所以,需要判断 B 是否为 A 的子结构时,可以依次遍历 A 中的所有结点,对每个在 A 中遍历到的结点依次做判断,判断该结点是否可以作为子结构 B 的根结点。
-
在代码中的两个函数:
- isSubStructure():用于遍历 A 中的所有结点,并调用 helper() 进行判断
- helper():用于判断 A 中当前结点能否作为 B 的根结点

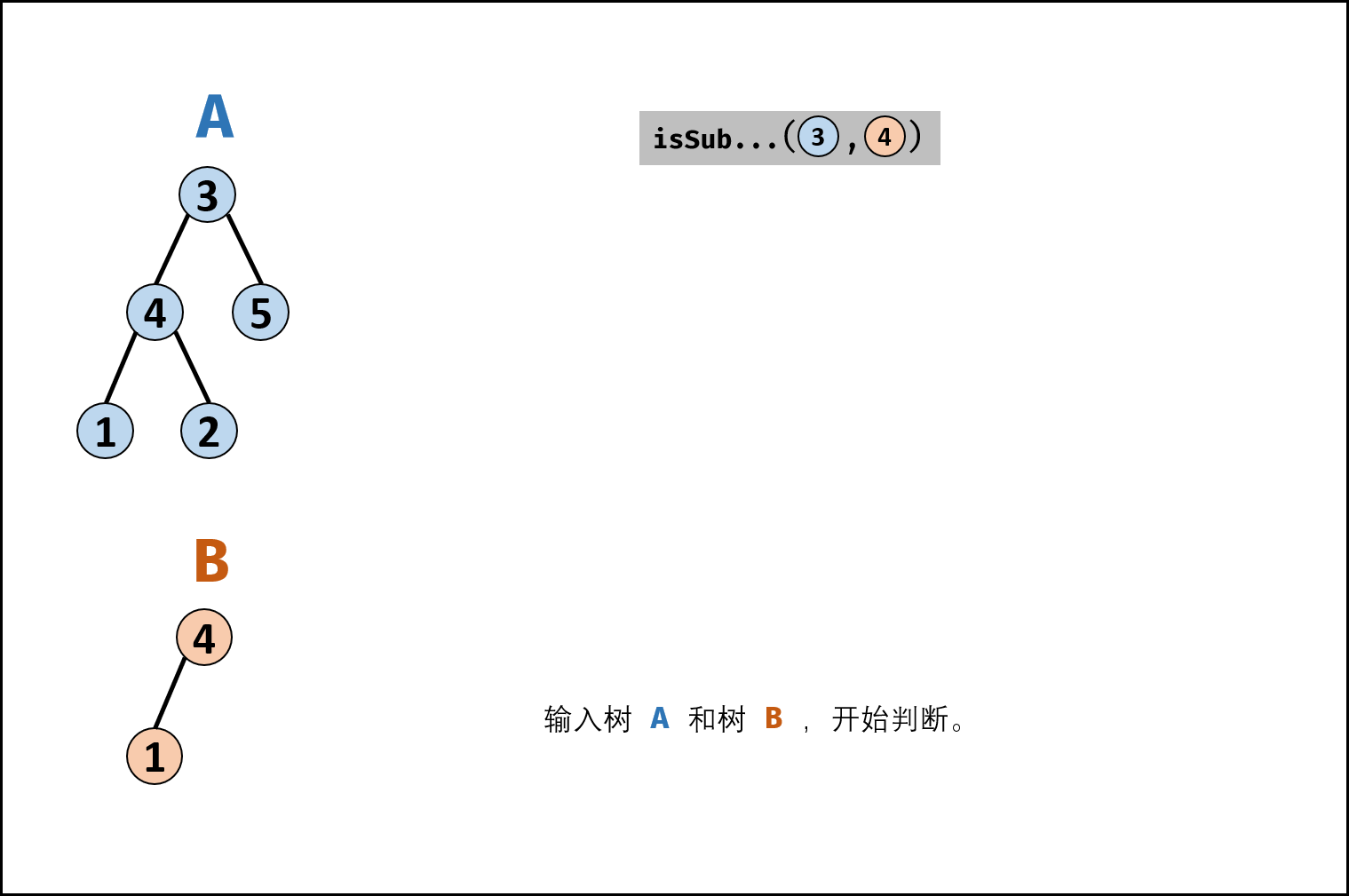


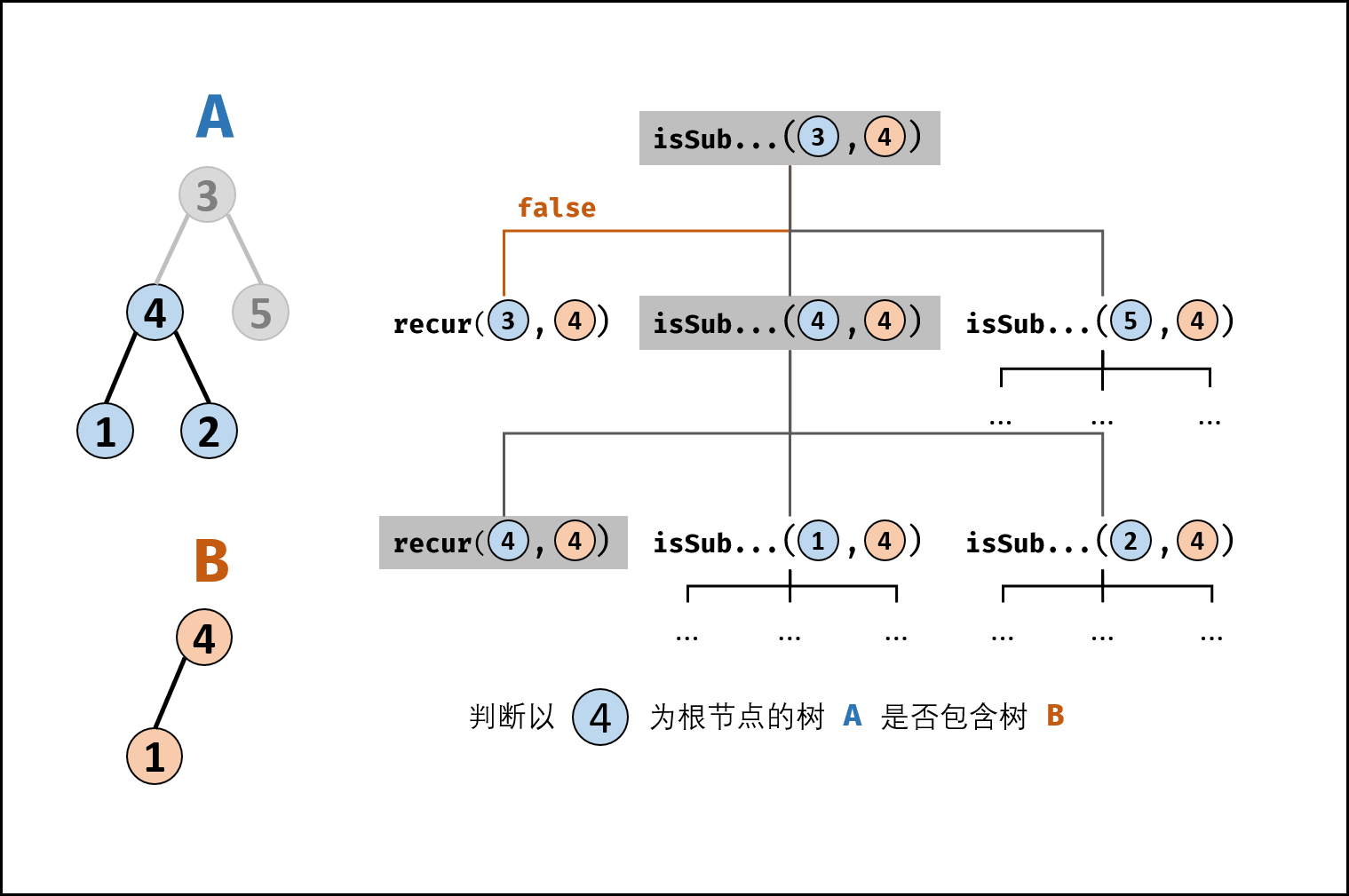

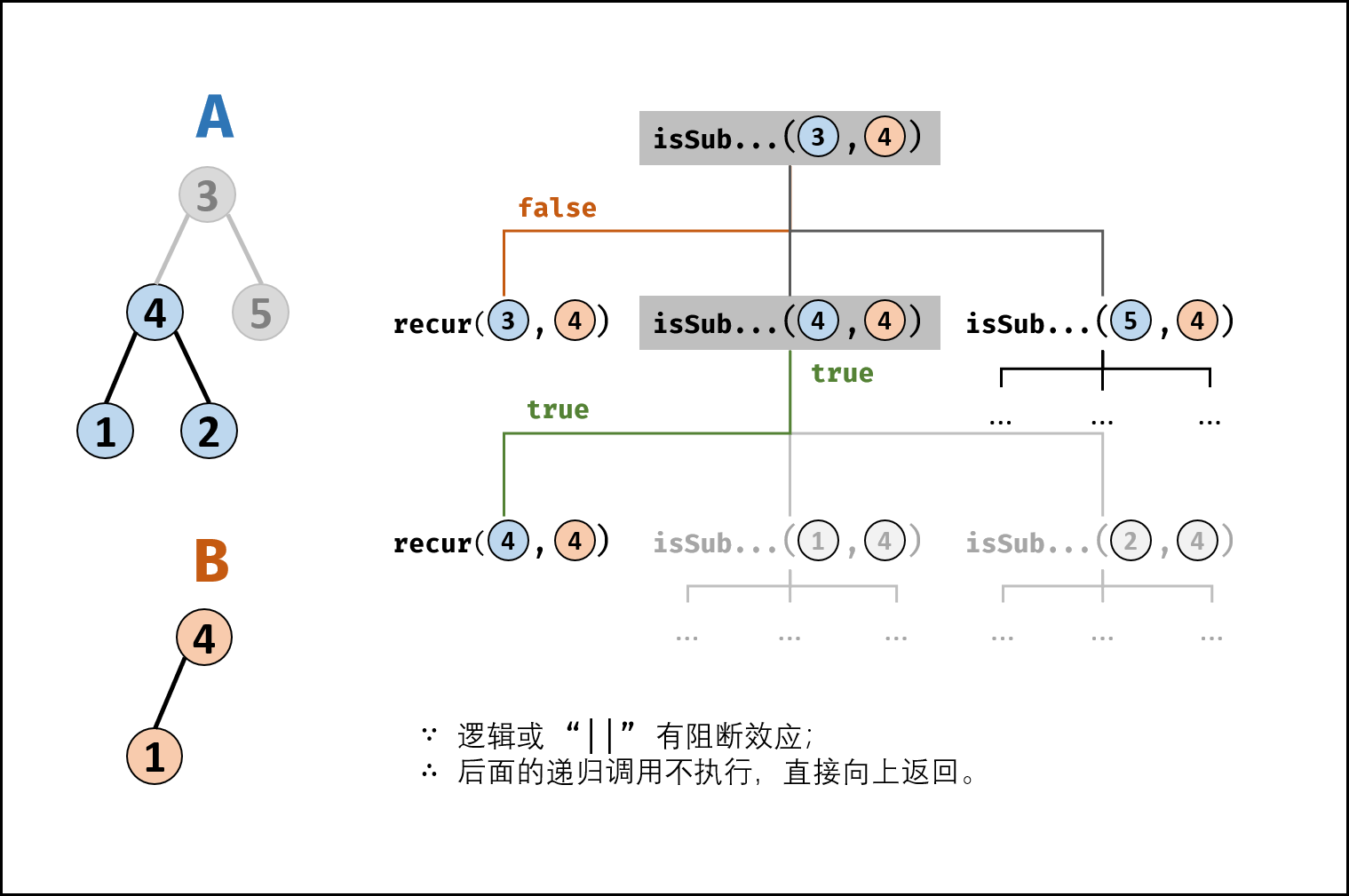


-
时间复杂度 O(MN) : 其中 M,N 分别为树 A 和 树 B 的节点数量;先序遍历树 A 占用 O(M) ,每次调用 help() 函数判断占用 O(N) 。
-
空间复杂度 O(M) : 当树 A 和树 B 都退化为链表时,递归调用深度最大。当 M≤N 时,遍历树 A 与递归判断的总递归深度为 M ;当 M>N 时,最差情况为遍历至树 A 叶子节点,此时总递归深度为 M 。
2.1.2 该题的伪代码
isSubStructure()
{
先序遍历 A 中所有结点
如果当前结点为 NULL 或者 B 为 NULL ,返回 false,因为题目约定,空树不是任意一个树的子结构
如果前面都不符合,调用helper()函数判断AB左右孩子是否相等
}
helper()
{
先序遍历 A 和 B
如果 B = NULL,说明 B 已遍历完,返回 true
如果 A = NULL,B ≠ NULL,说明 A 中结点不足以构成子结构 B,返回 false
如果 A->val ≠ B->val,不满足结点值相等条件,返回 false
}
2.1.3 运行结果

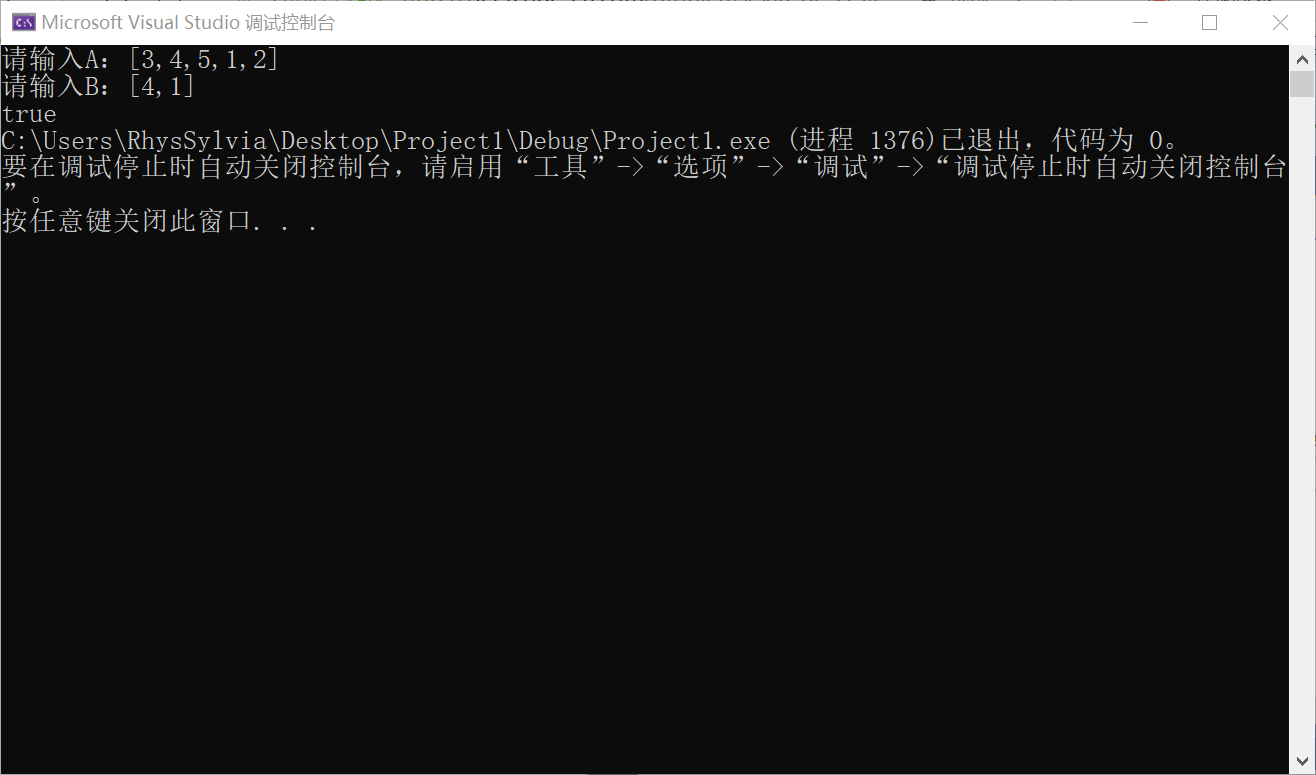
2.1.4 分析该题目解题优势及难点
- 这道题的思路比较清晰,先遍历A树,在A中找到B的根结点后,再去判断AB的孩子是否一样即可
- 比较麻烦的地方就是当树A中的节点为空,但树B中的节点不为空时,这种false的情况容易忽略
2.2 N叉树的层序遍历
- 题目
给定一个 N 叉树,返回其节点值的层序遍历。 (即从左到右,逐层遍历)。
例如,给定一个 3叉树 :
1
/ | \
3 2 4
/ \
5 6
返回其层序遍历:
[
[1],
[3,2,4],
[5,6]
]
说明:
树的深度不会超过 1000。
树的节点总数不会超过 5000。
- 代码
/*
// Definition for a Node.
class Node {
public:
int val;
vector<Node*> children;
Node() {}
Node(int _val) {
val = _val;
}
Node(int _val, vector<Node*> _children) {
val = _val;
children = _children;
}
};
*/
class Solution {
public:
vector<vector<int>> levelOrder(Node* root) {
vector<vector<int>> ans;
if(!root)
return ans;
queue<Node*> q;
q.push(root);
while(!q.empty()){
vector<int> tmp;
int size = q.size();
while(size--){
Node* node = q.front();
for(int i = 0; i < node->children.size(); i++){
q.push(node->children[i]);
}
tmp.push_back(node->val);
q.pop();
}
ans.push_back(tmp);
}
return ans;
}
};
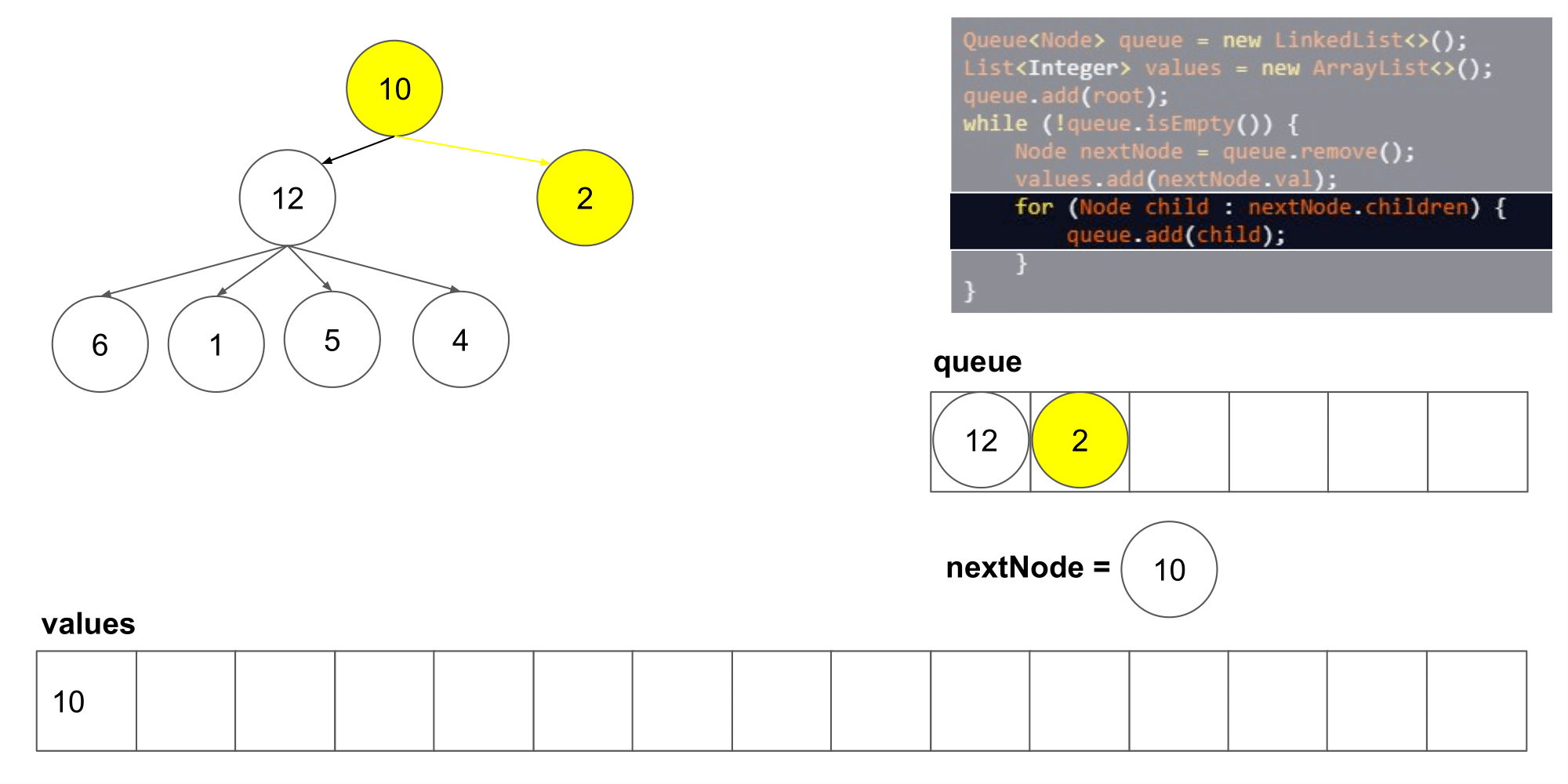
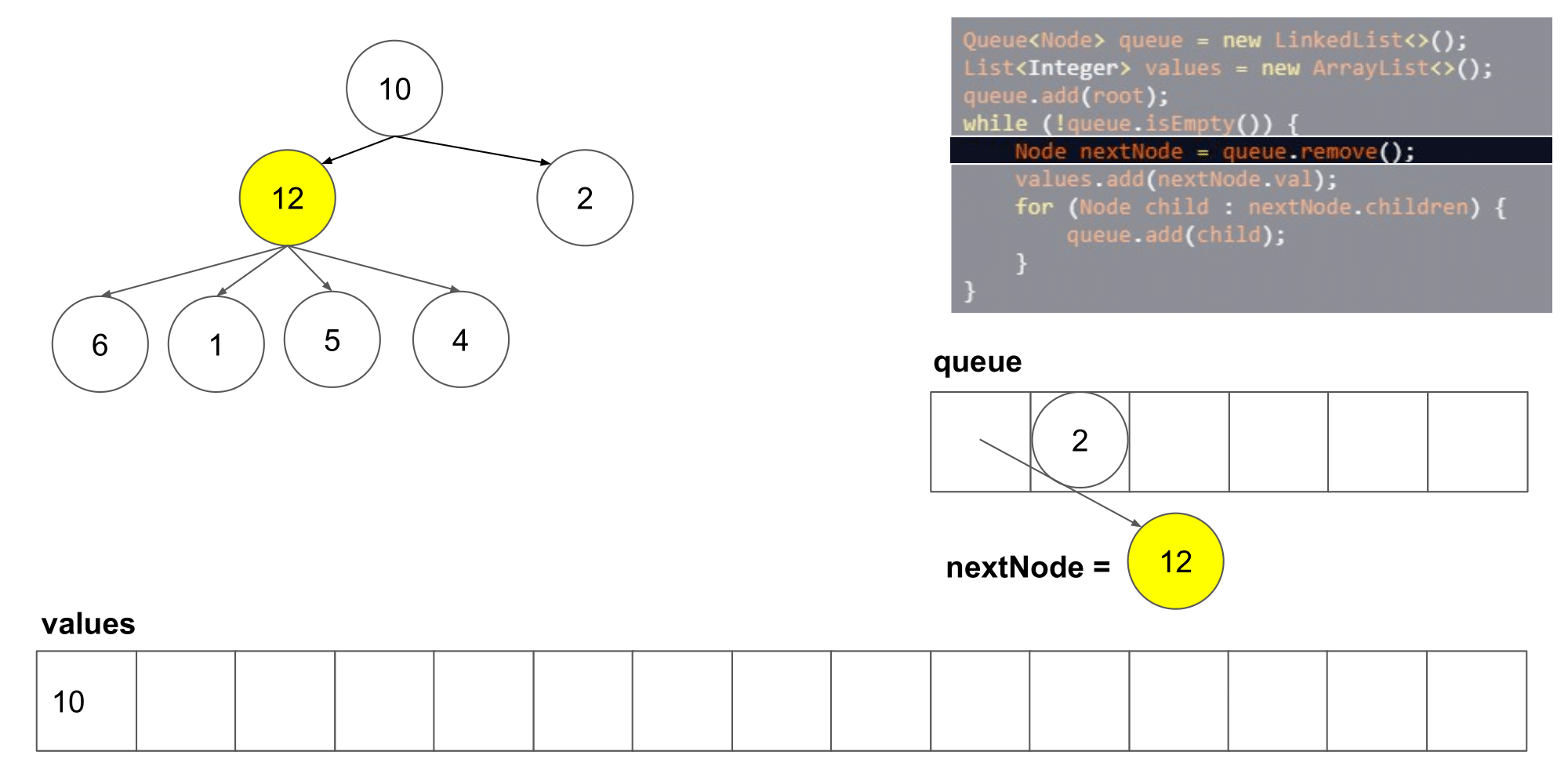
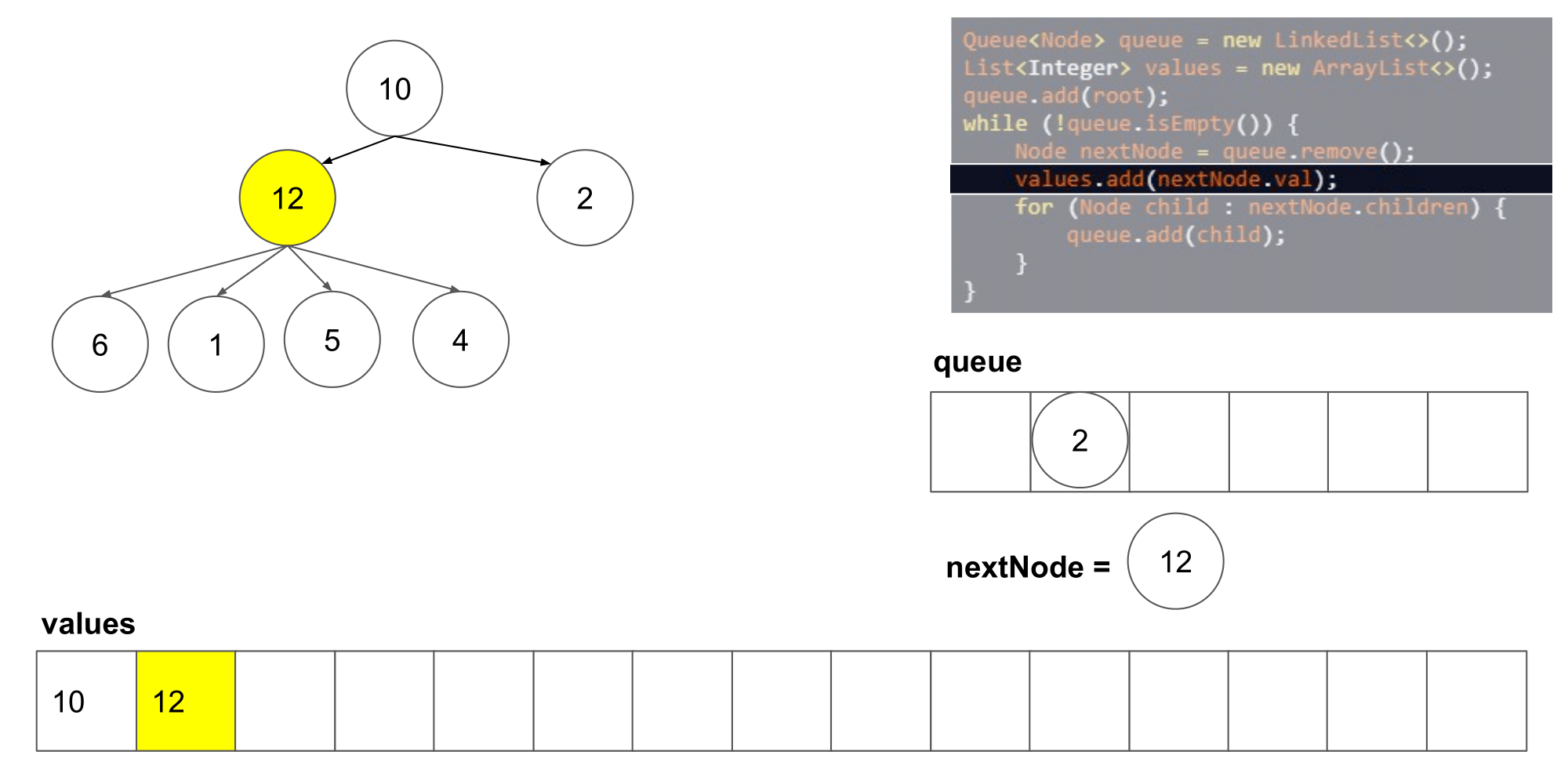
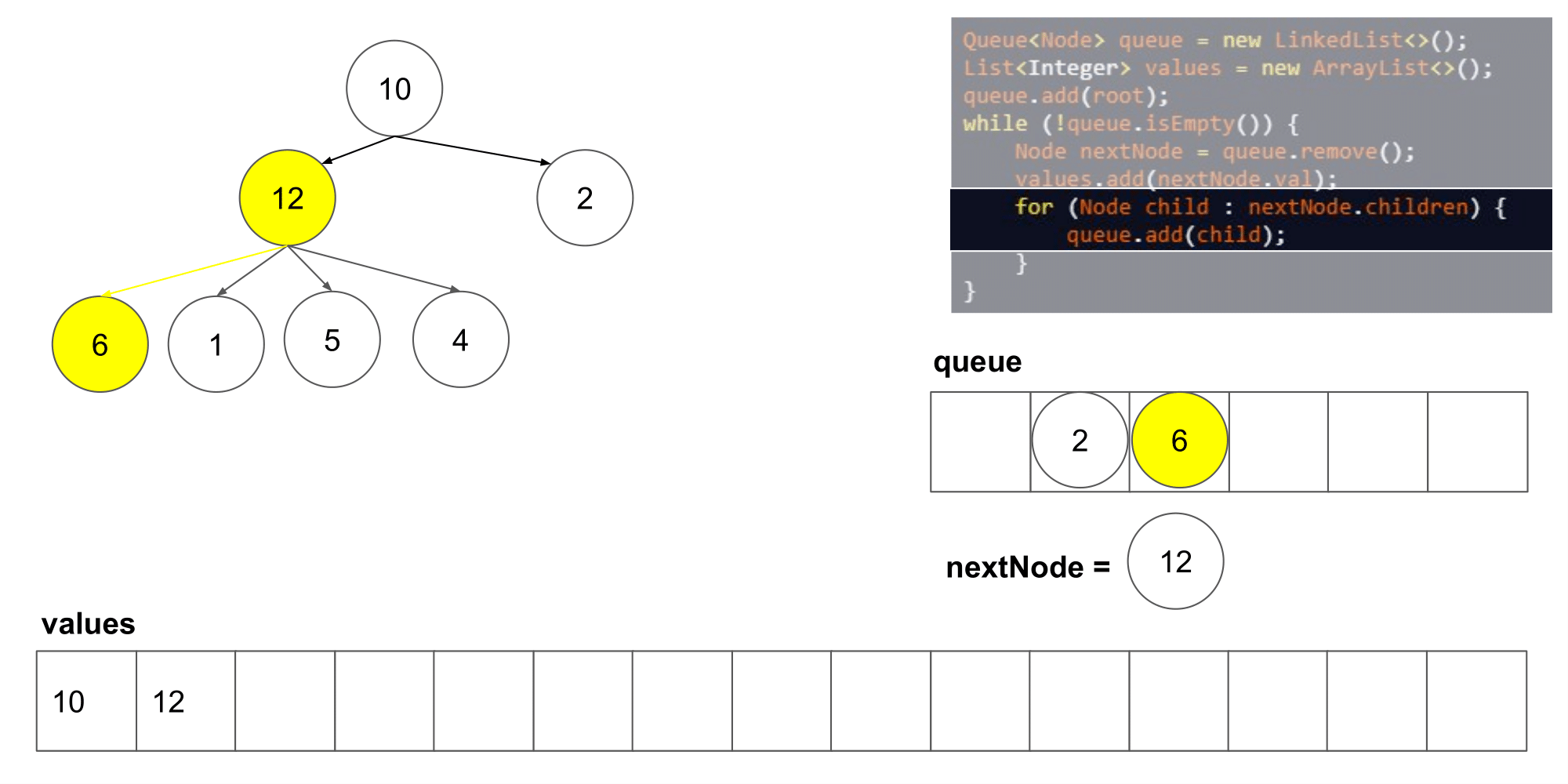
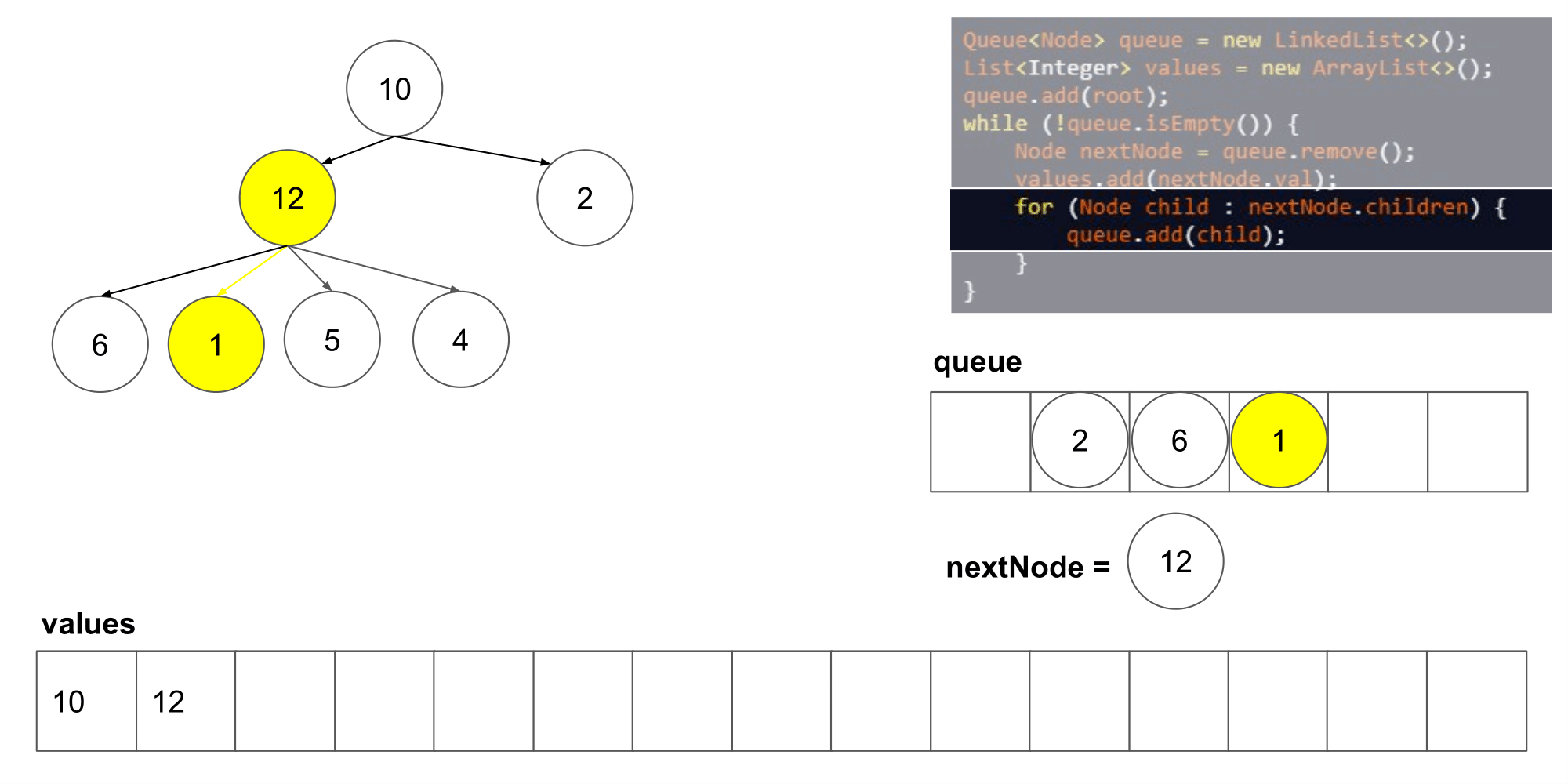
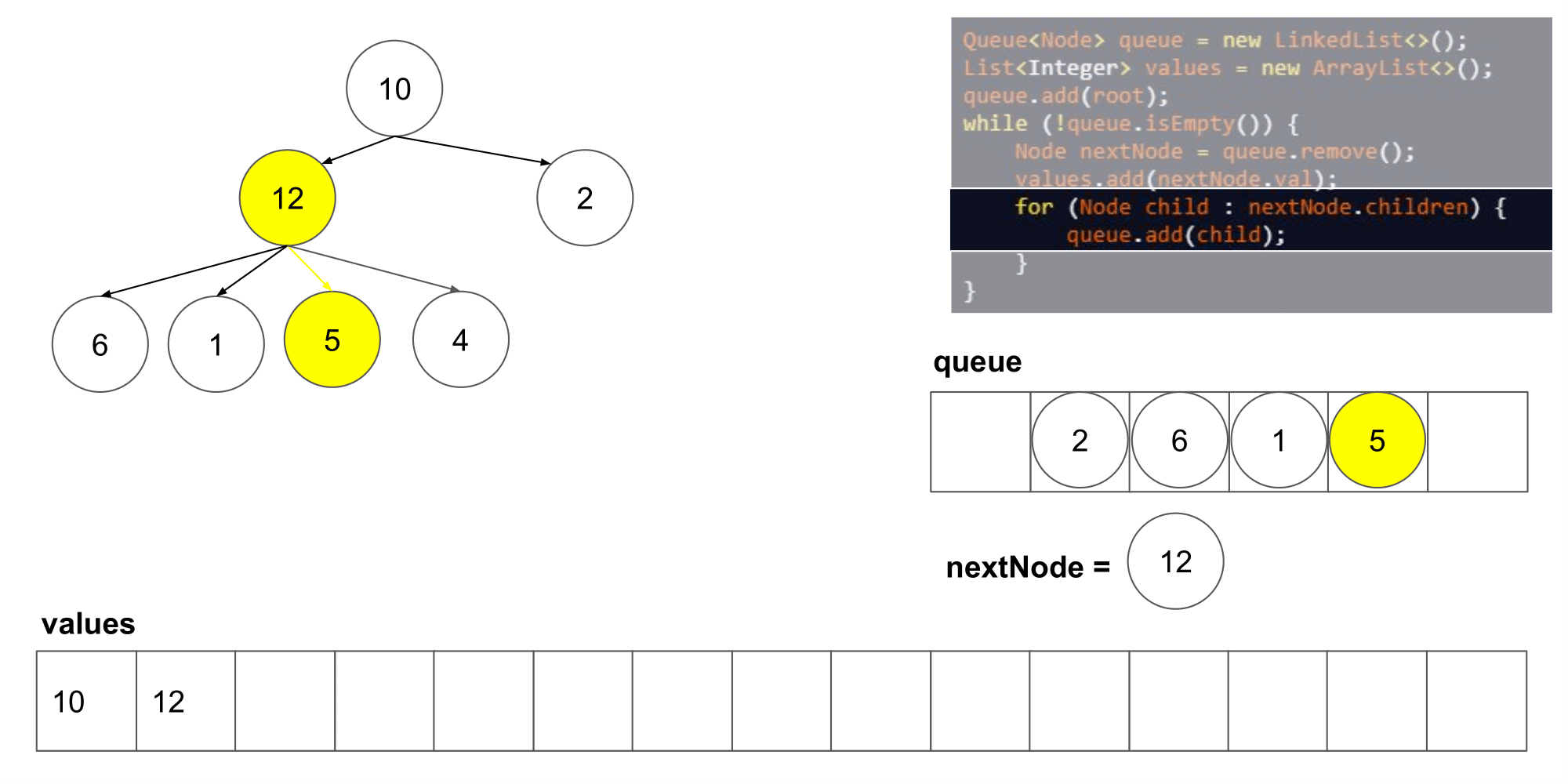
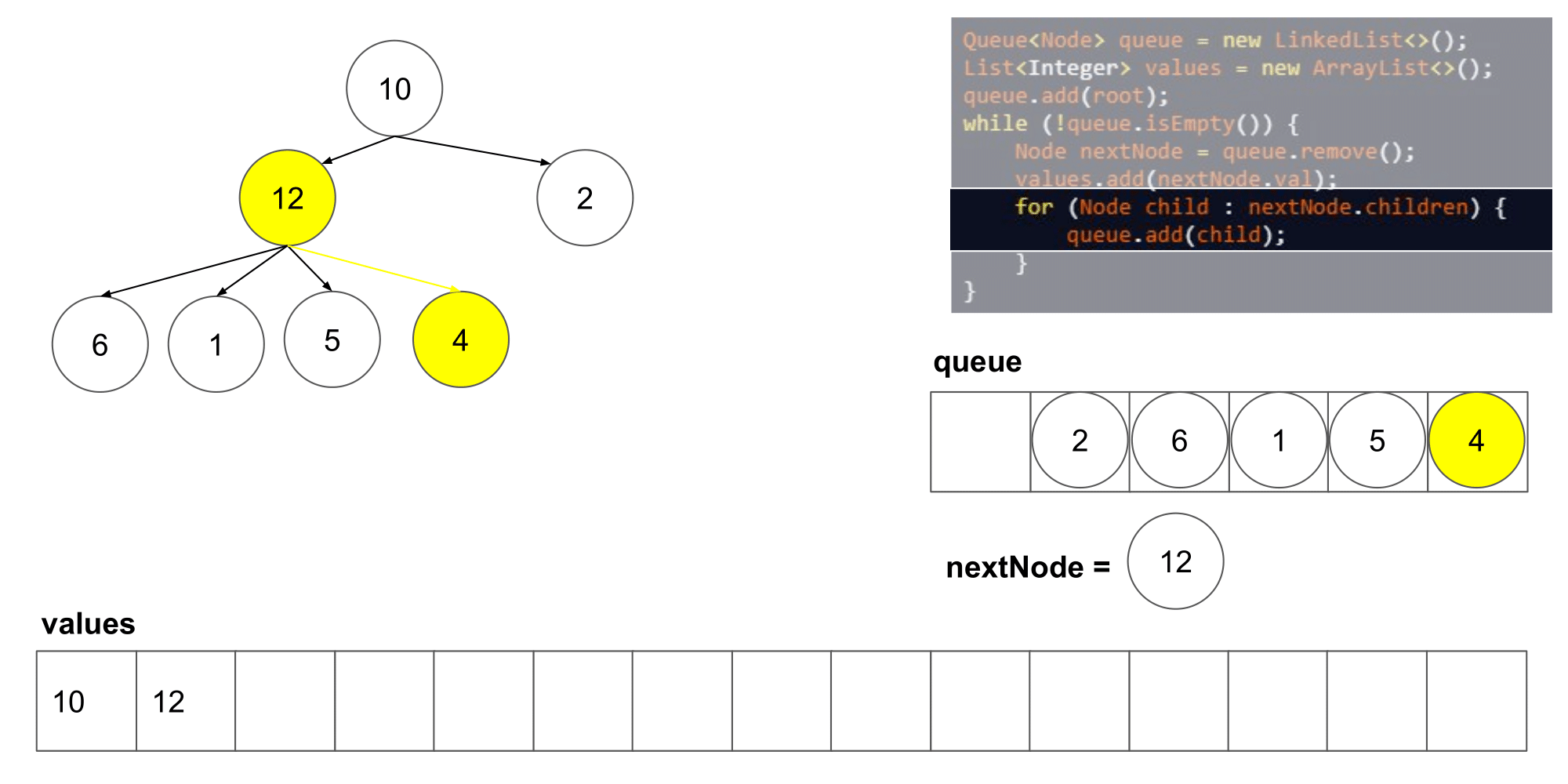
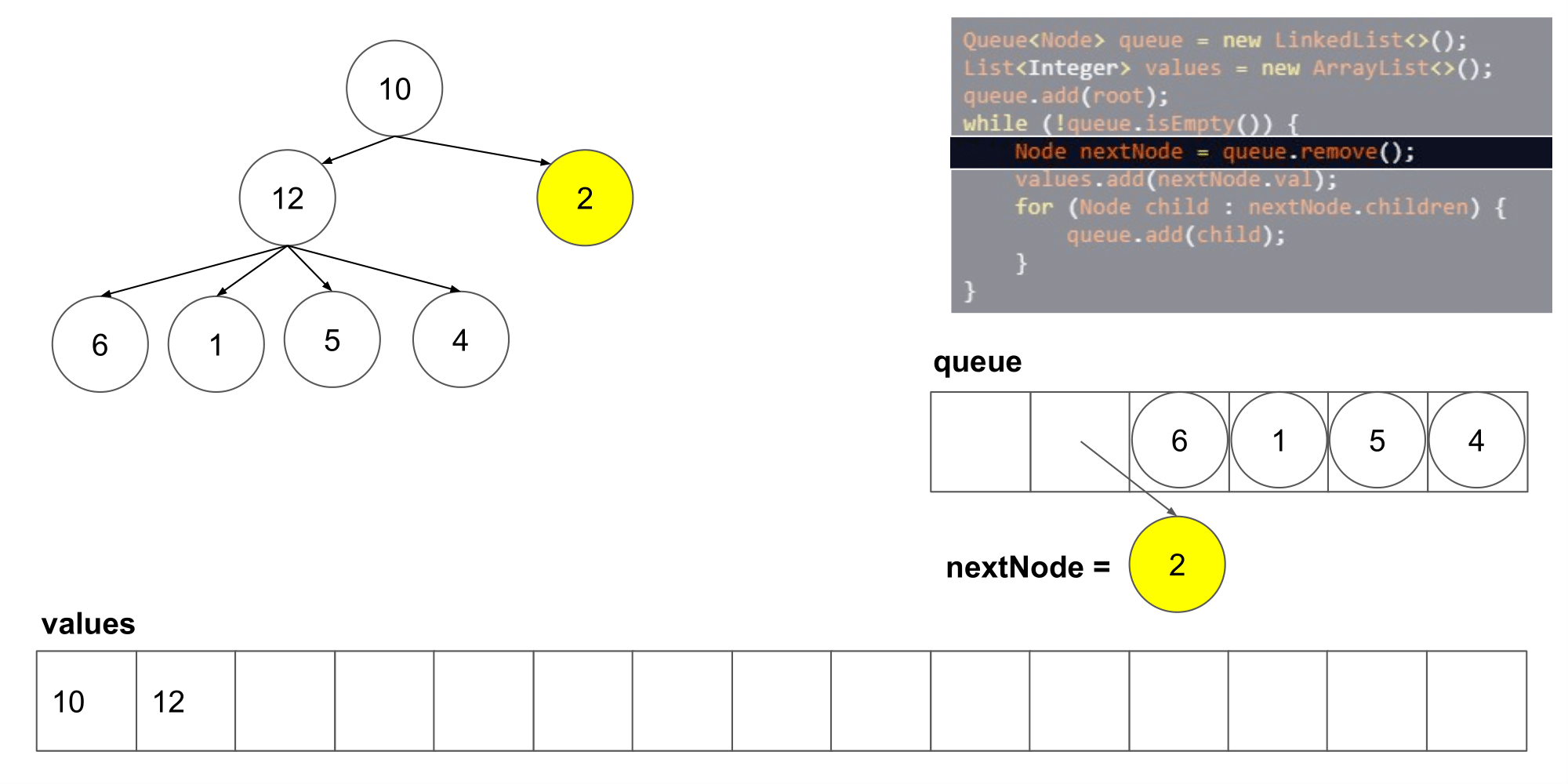
2.2.1 该题的设计思路
-
这道题其实类似于二叉树的层次遍历,但是是将父结点的两个孩子变成了几个孩子,遍历树时,先入队列root根节点,然后,分层次遍历根节点的孩子们,将他们入队列,然后出队列继续遍历下一层即可
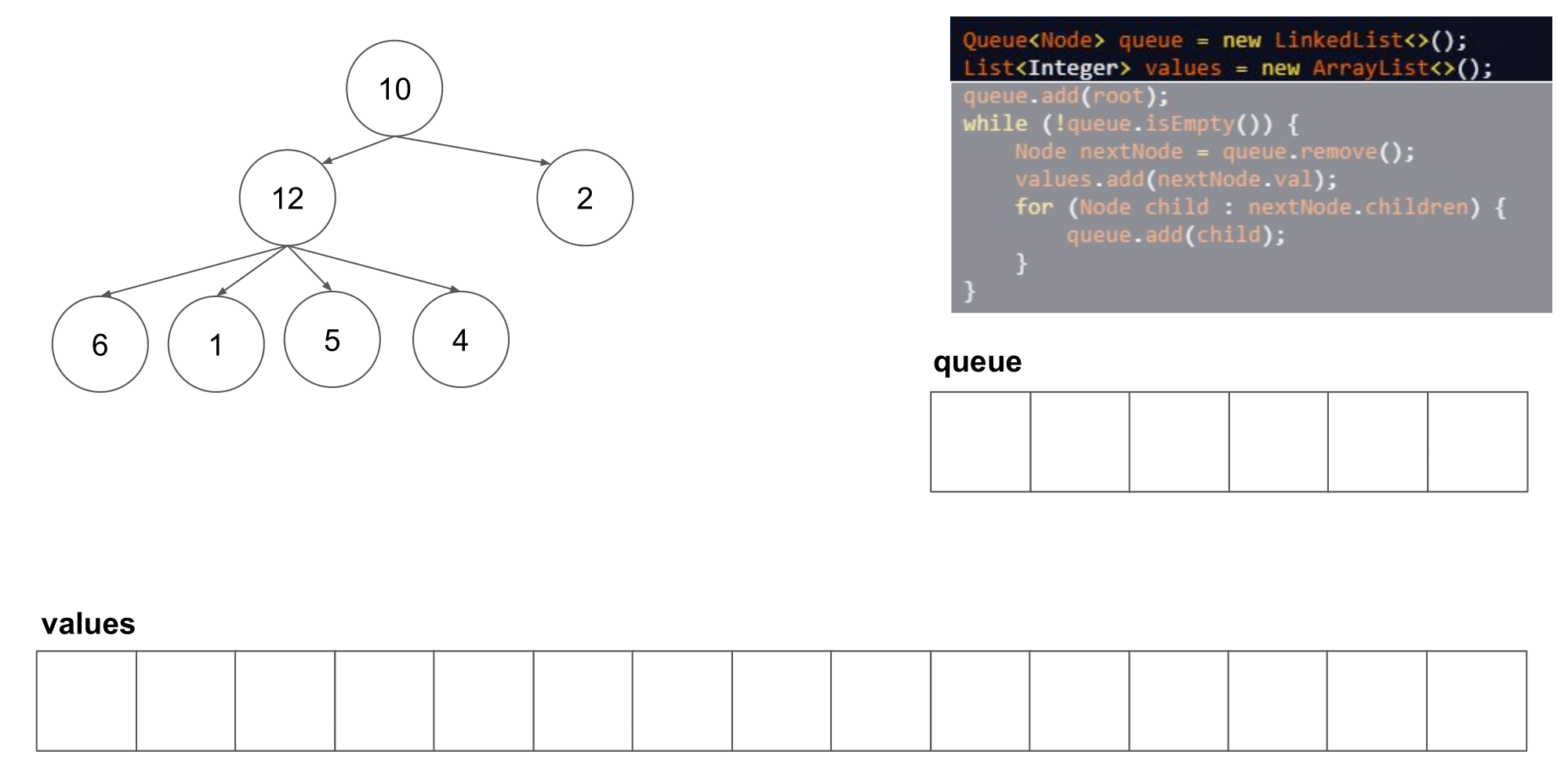
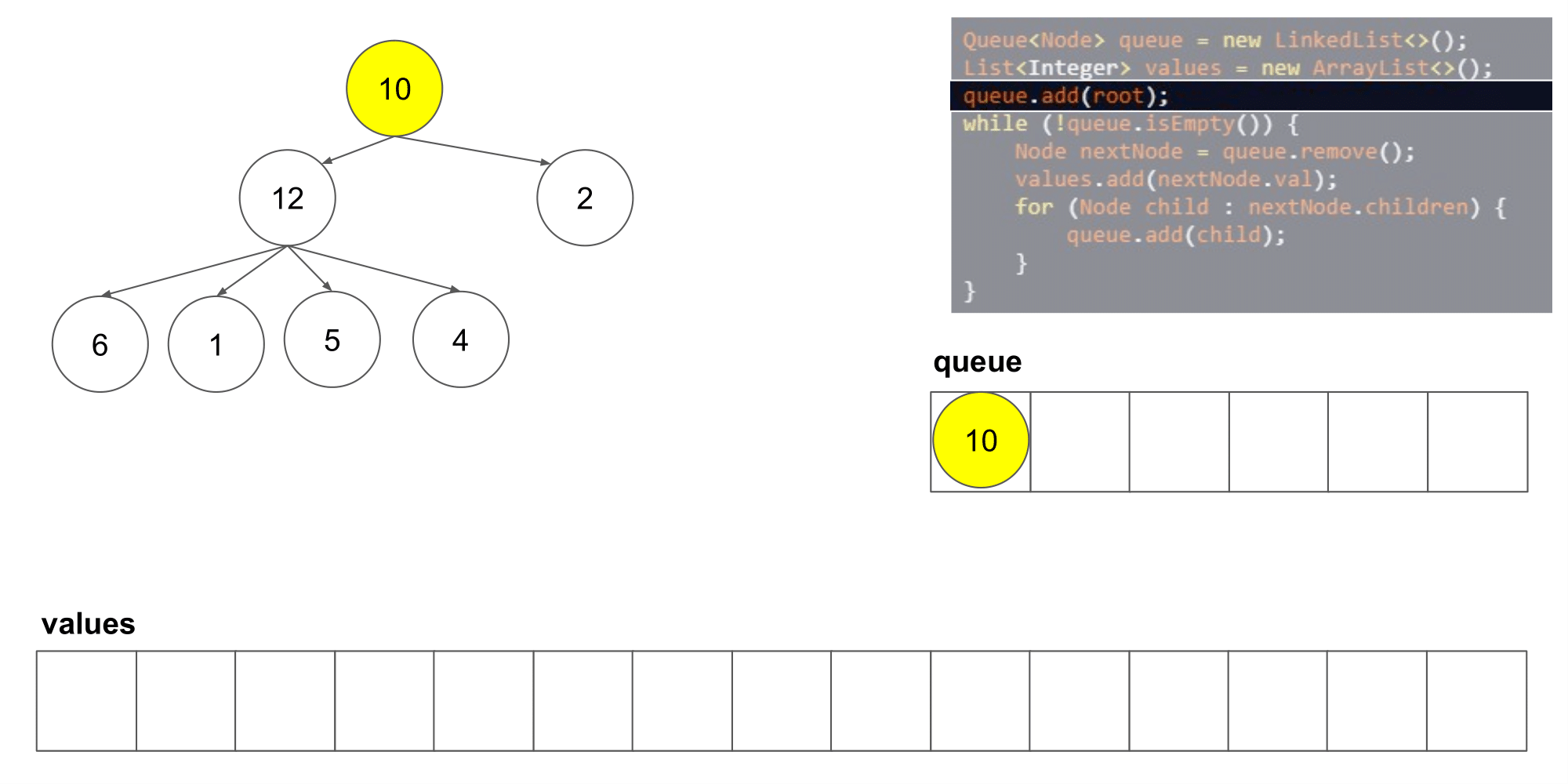
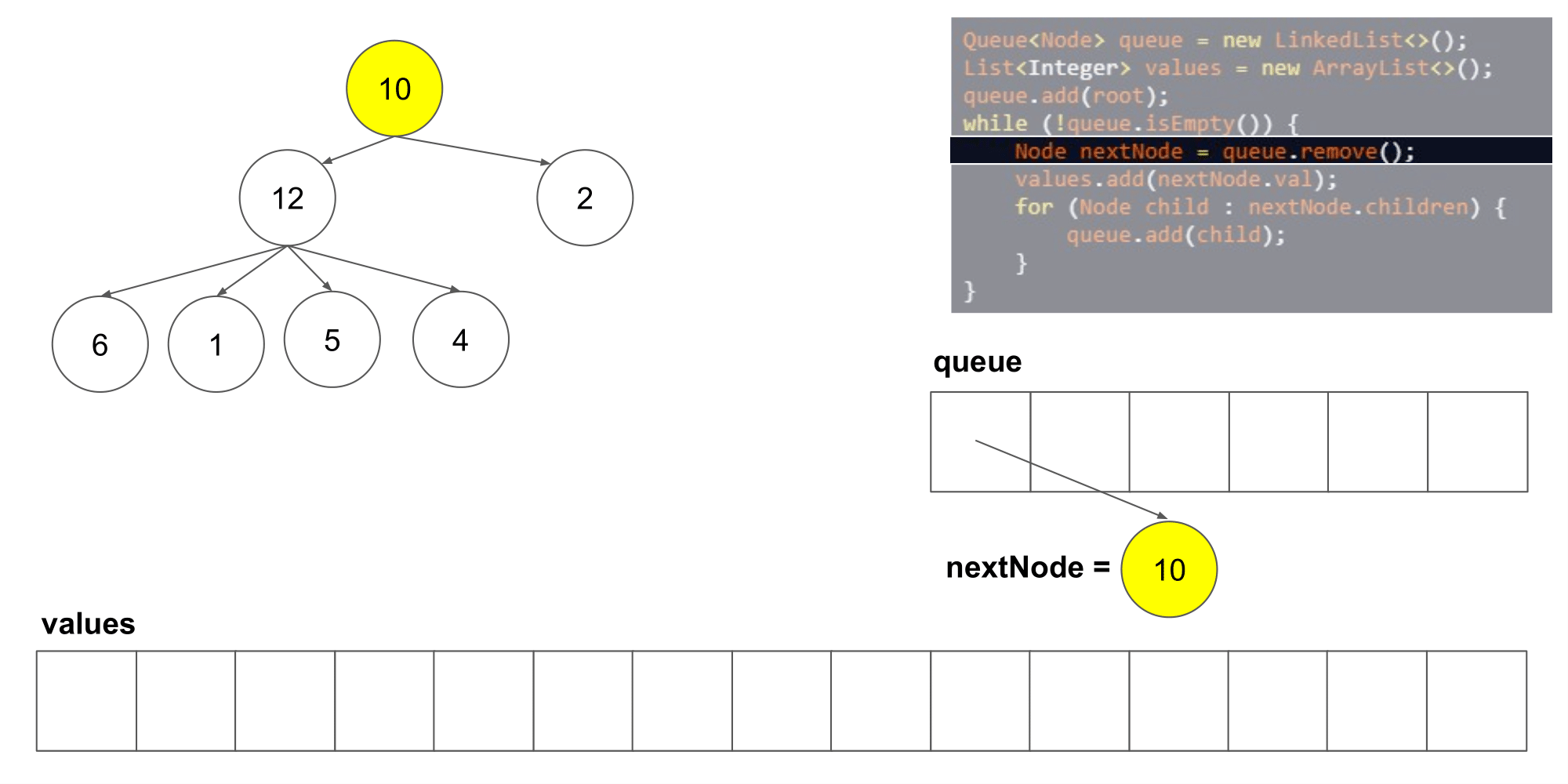
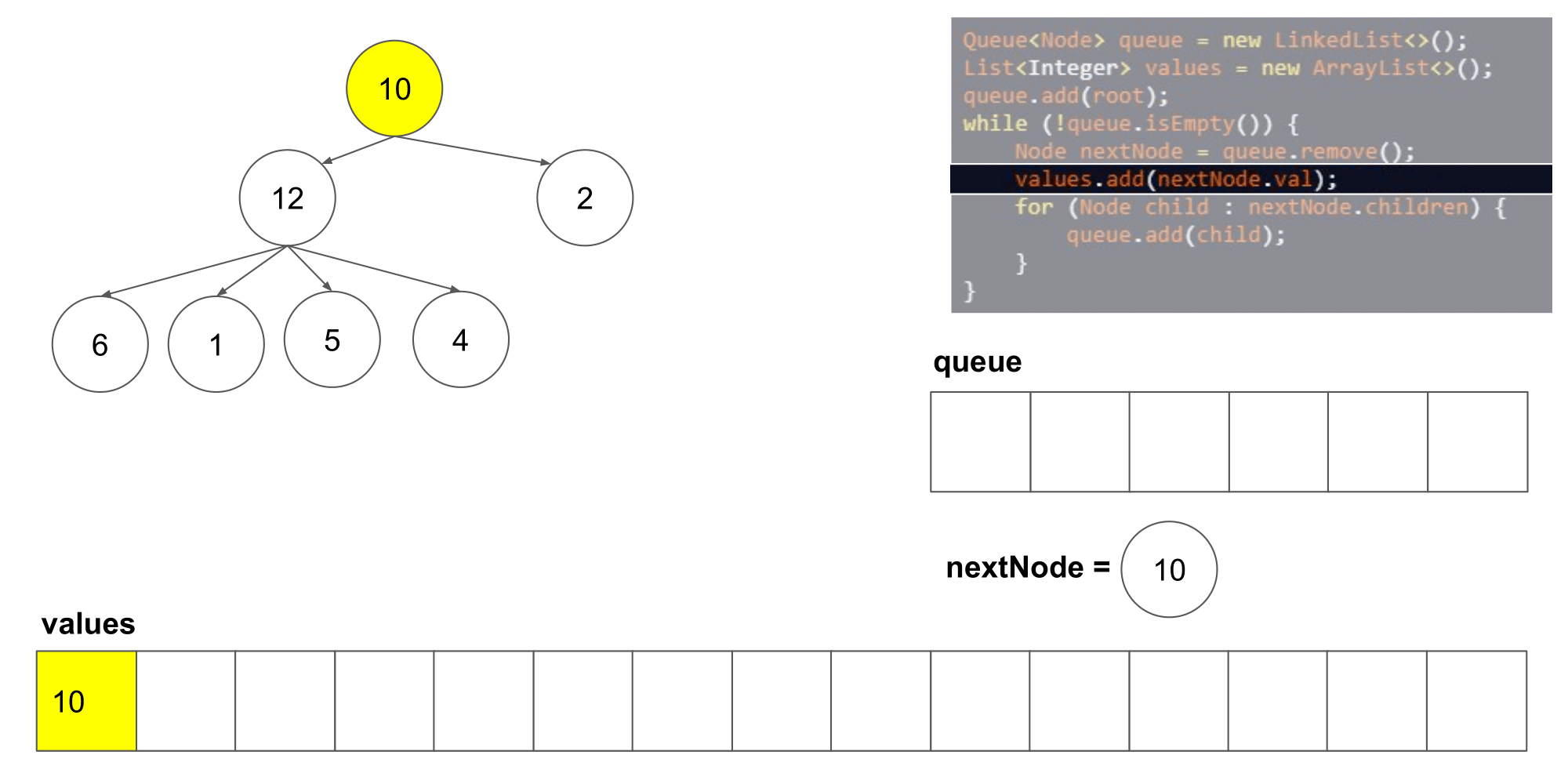
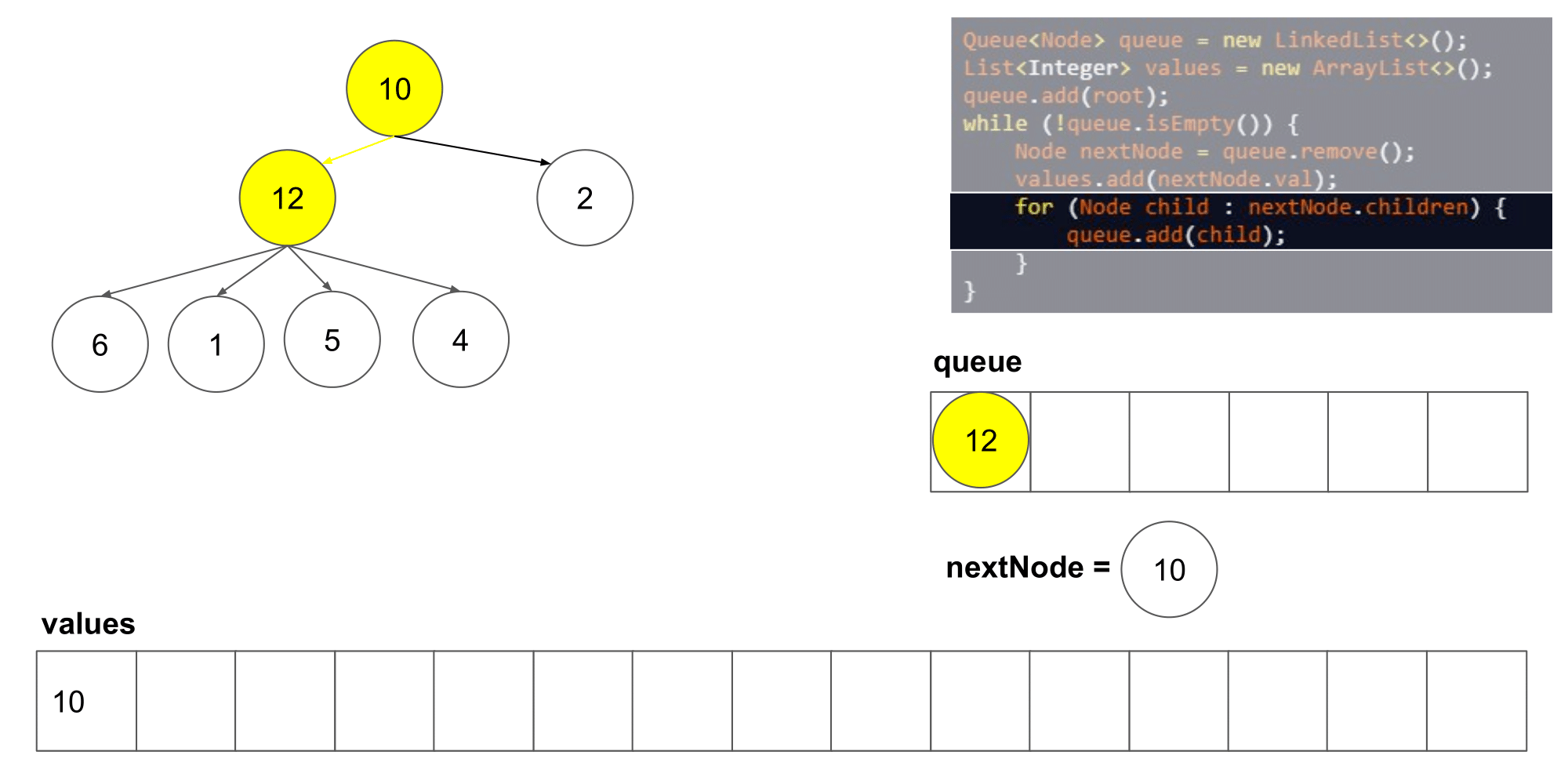
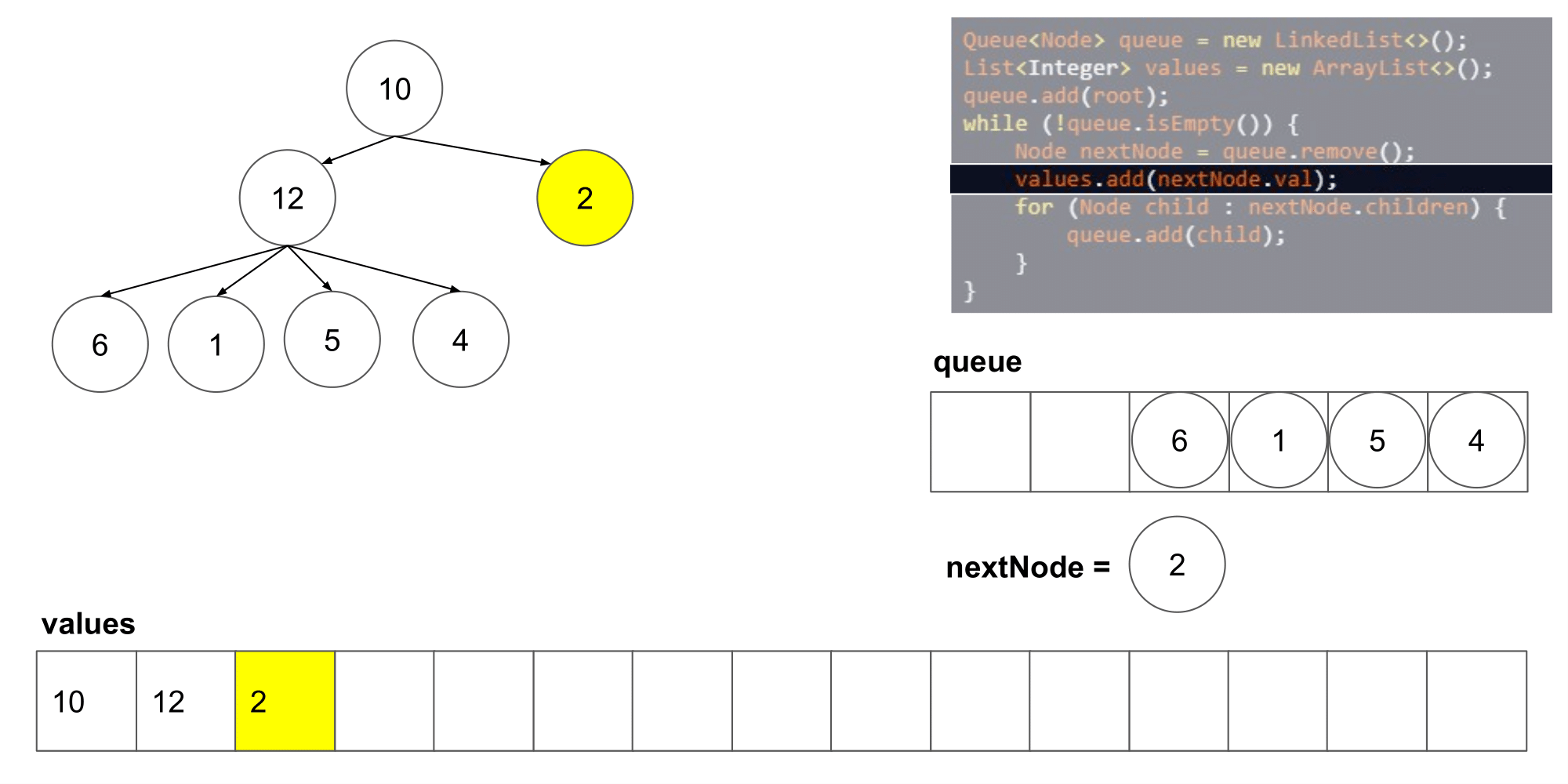

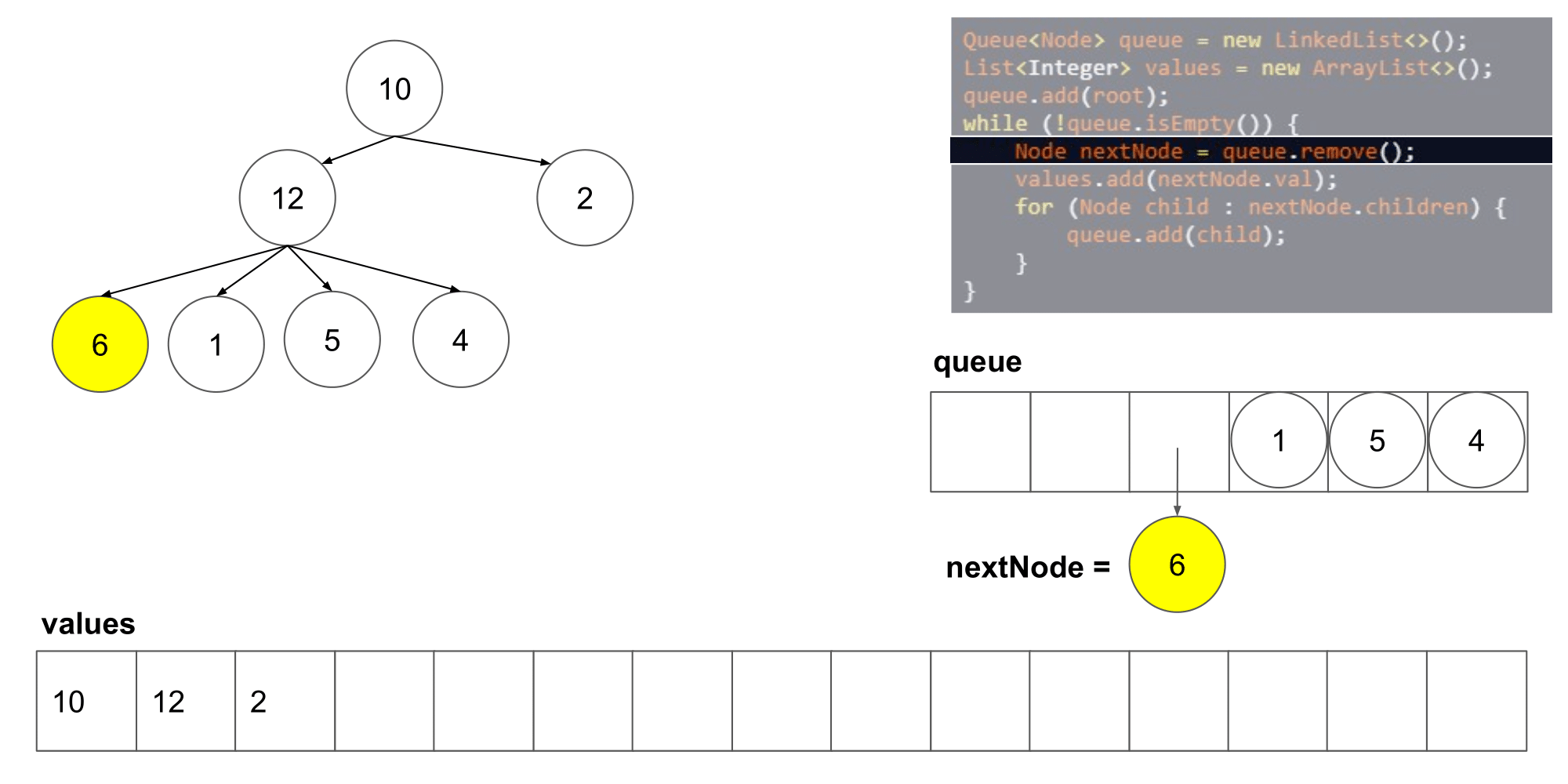
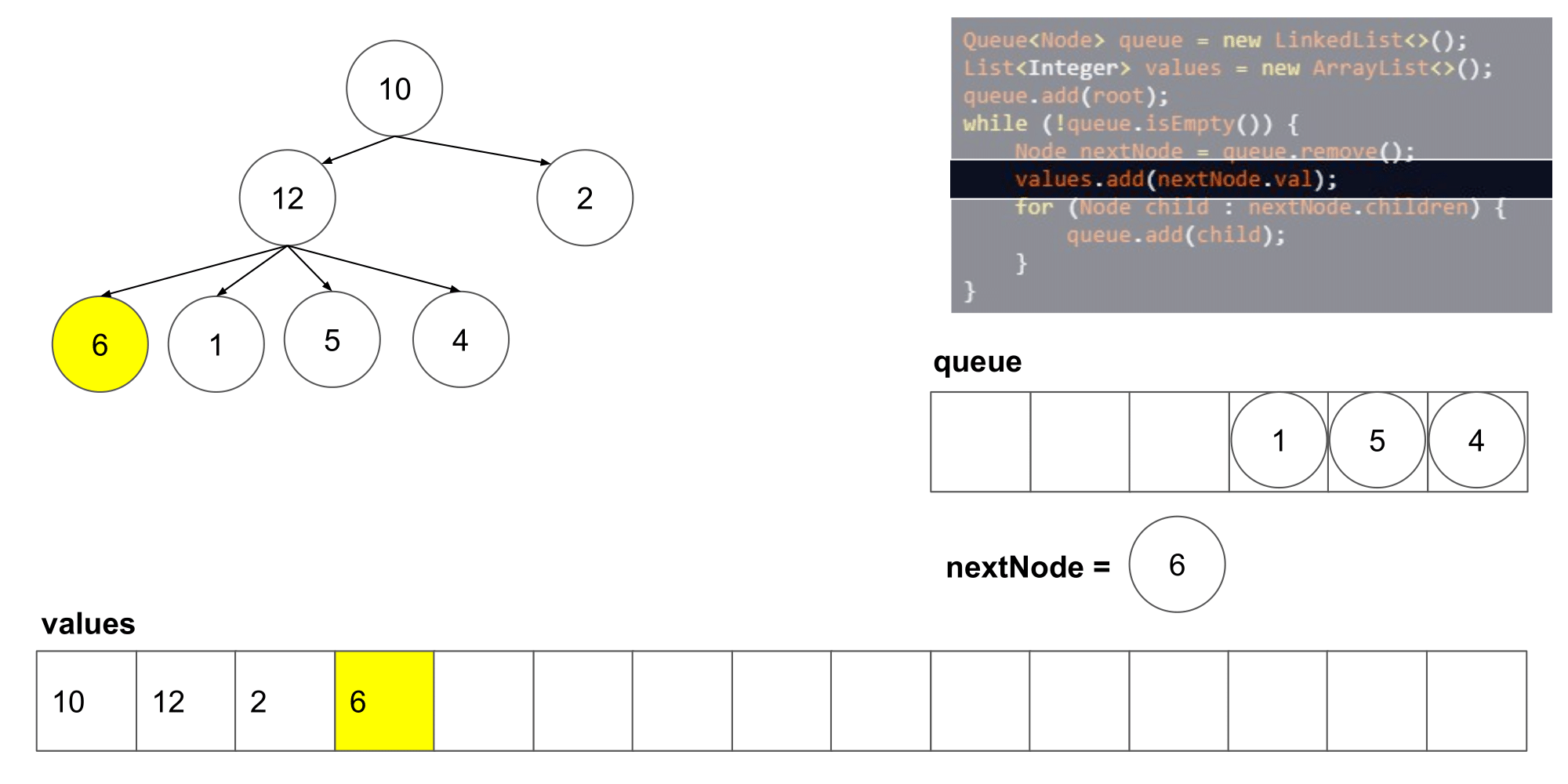
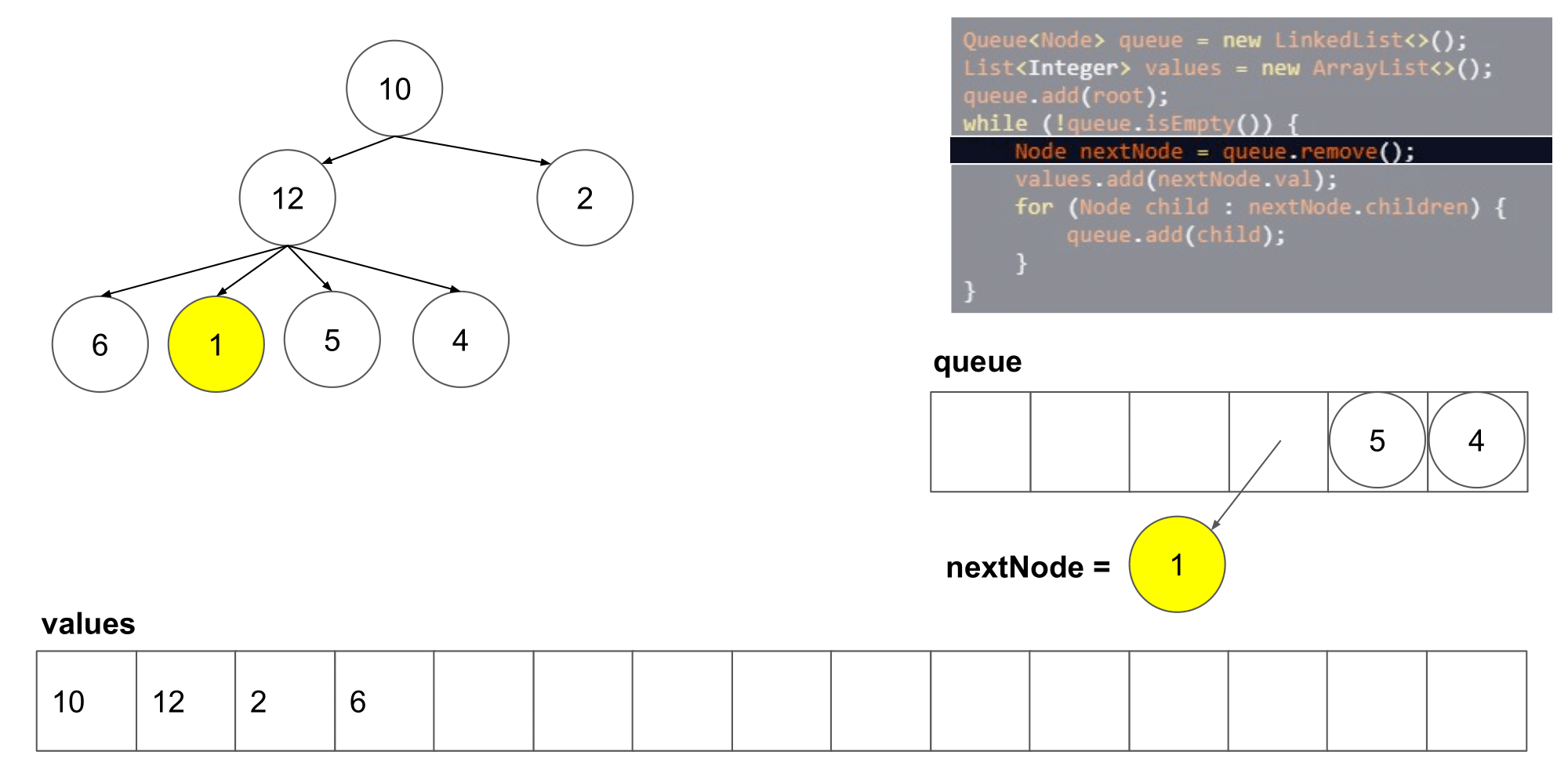
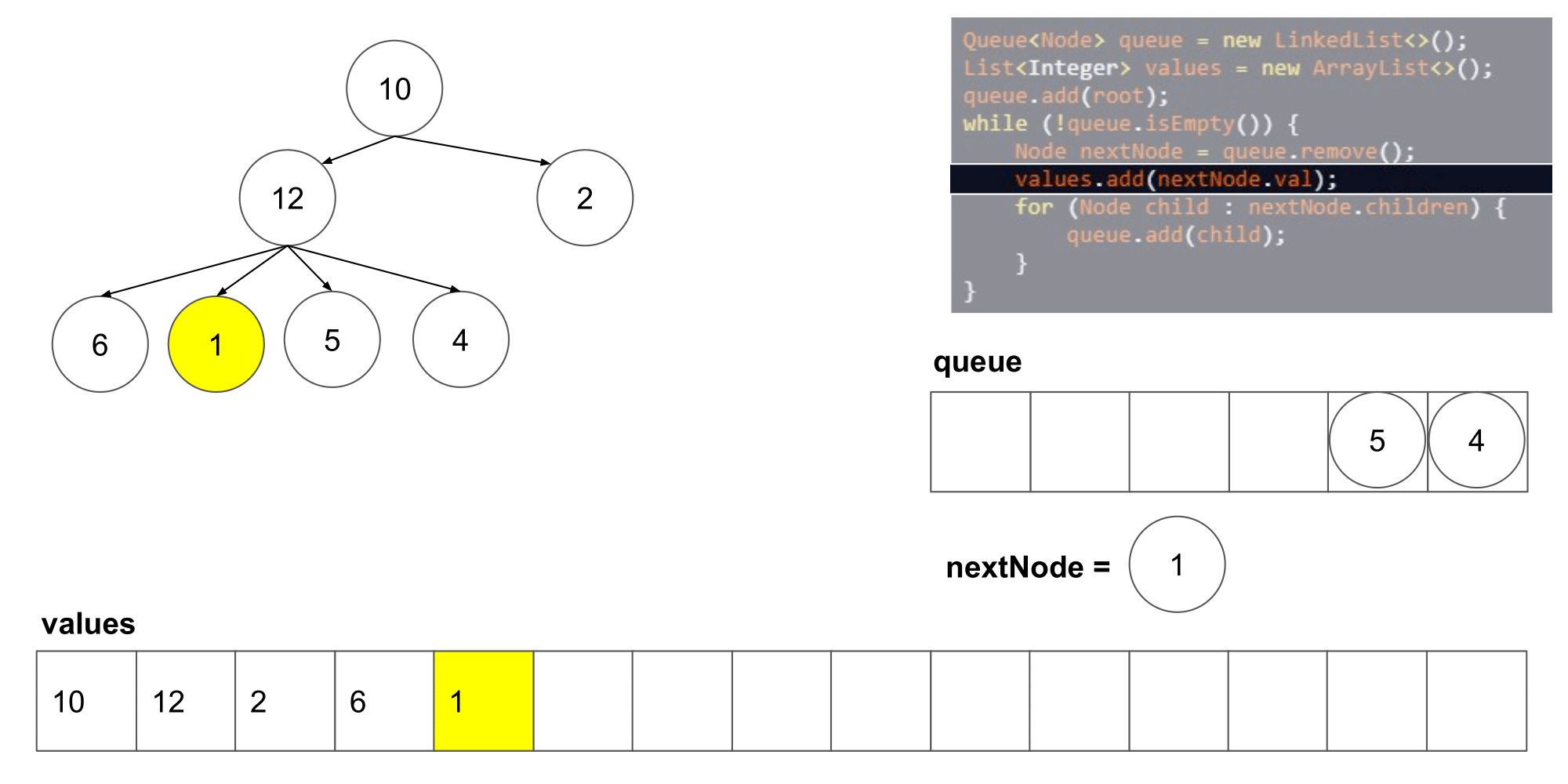
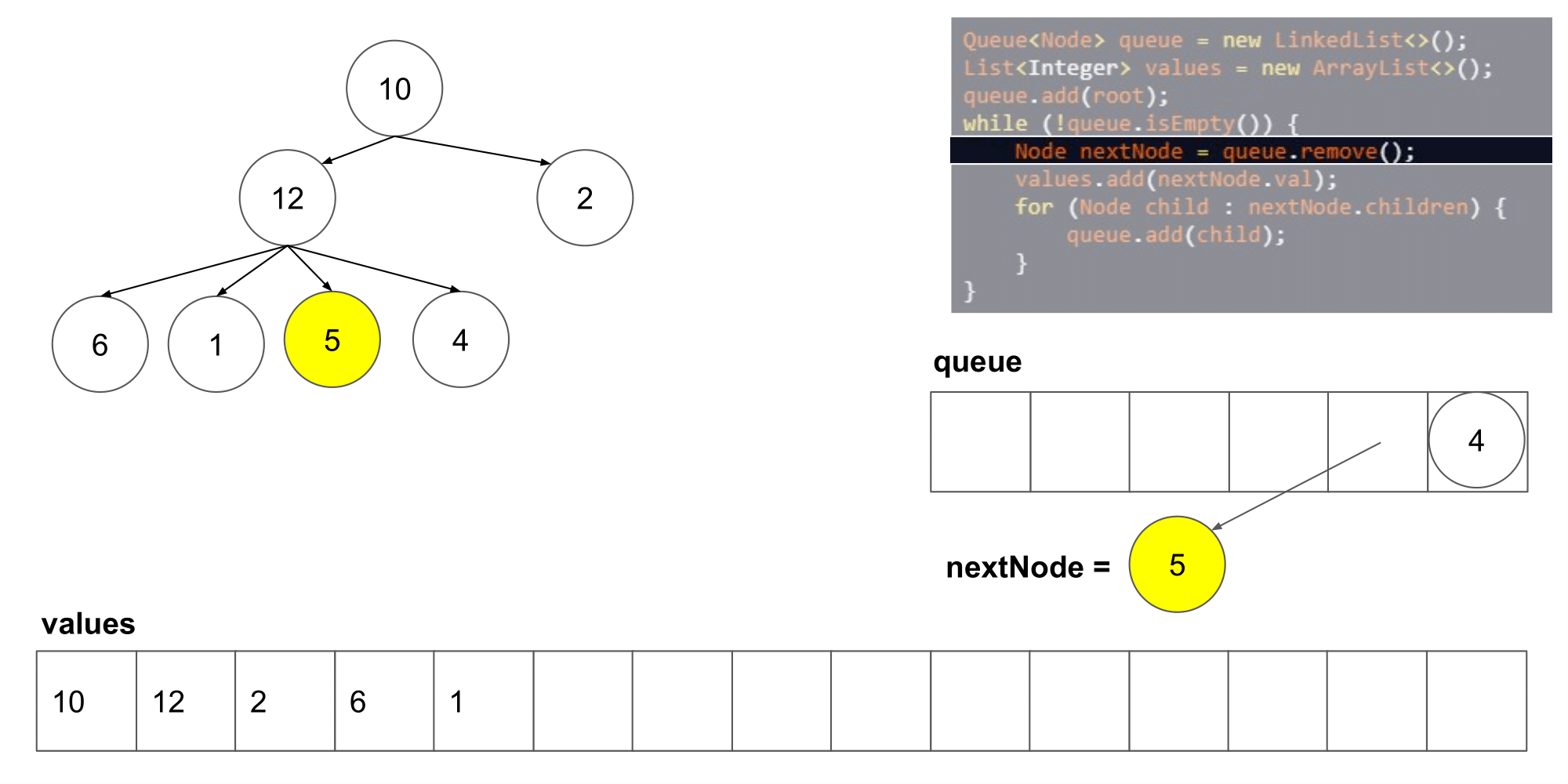
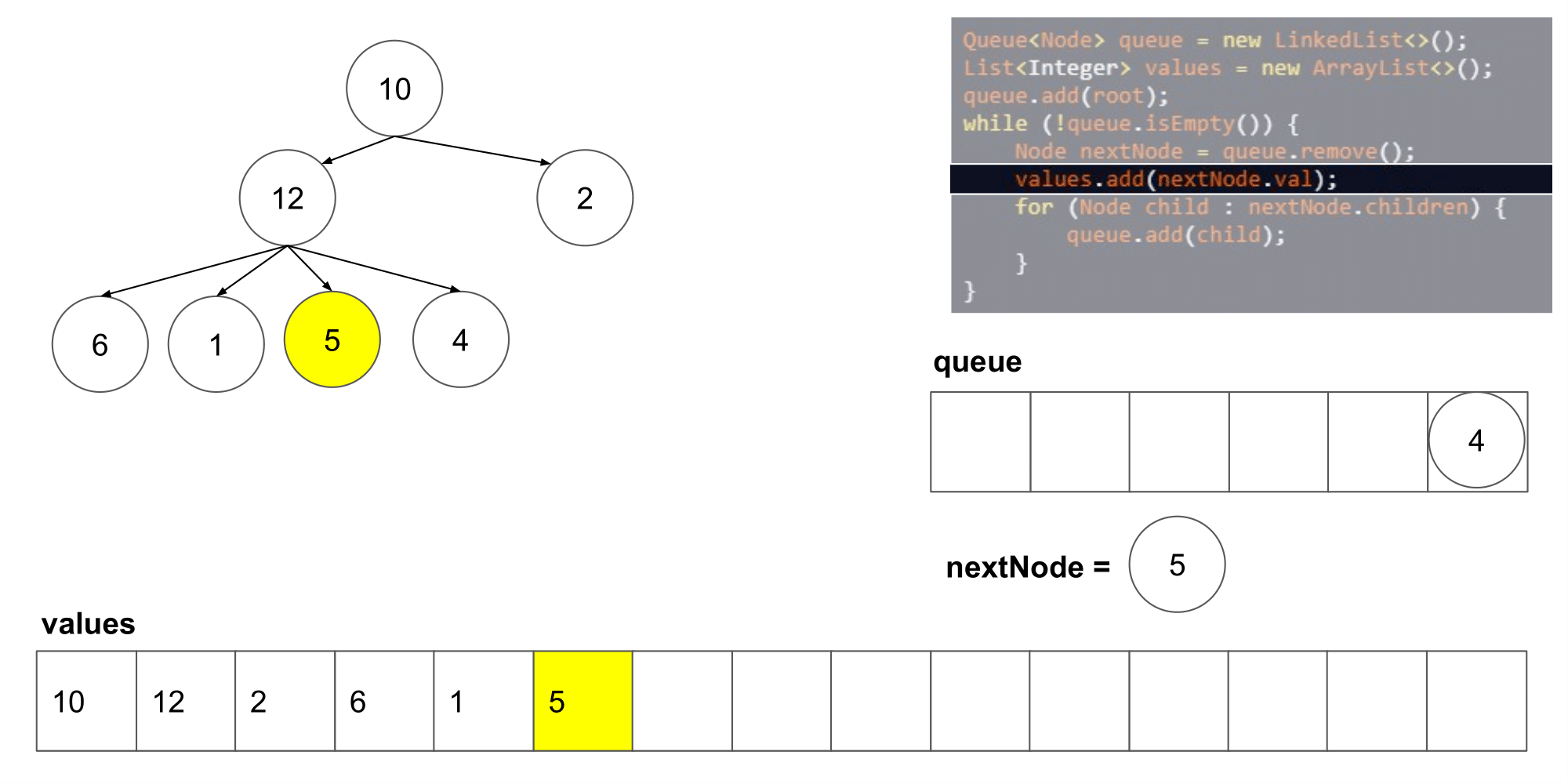

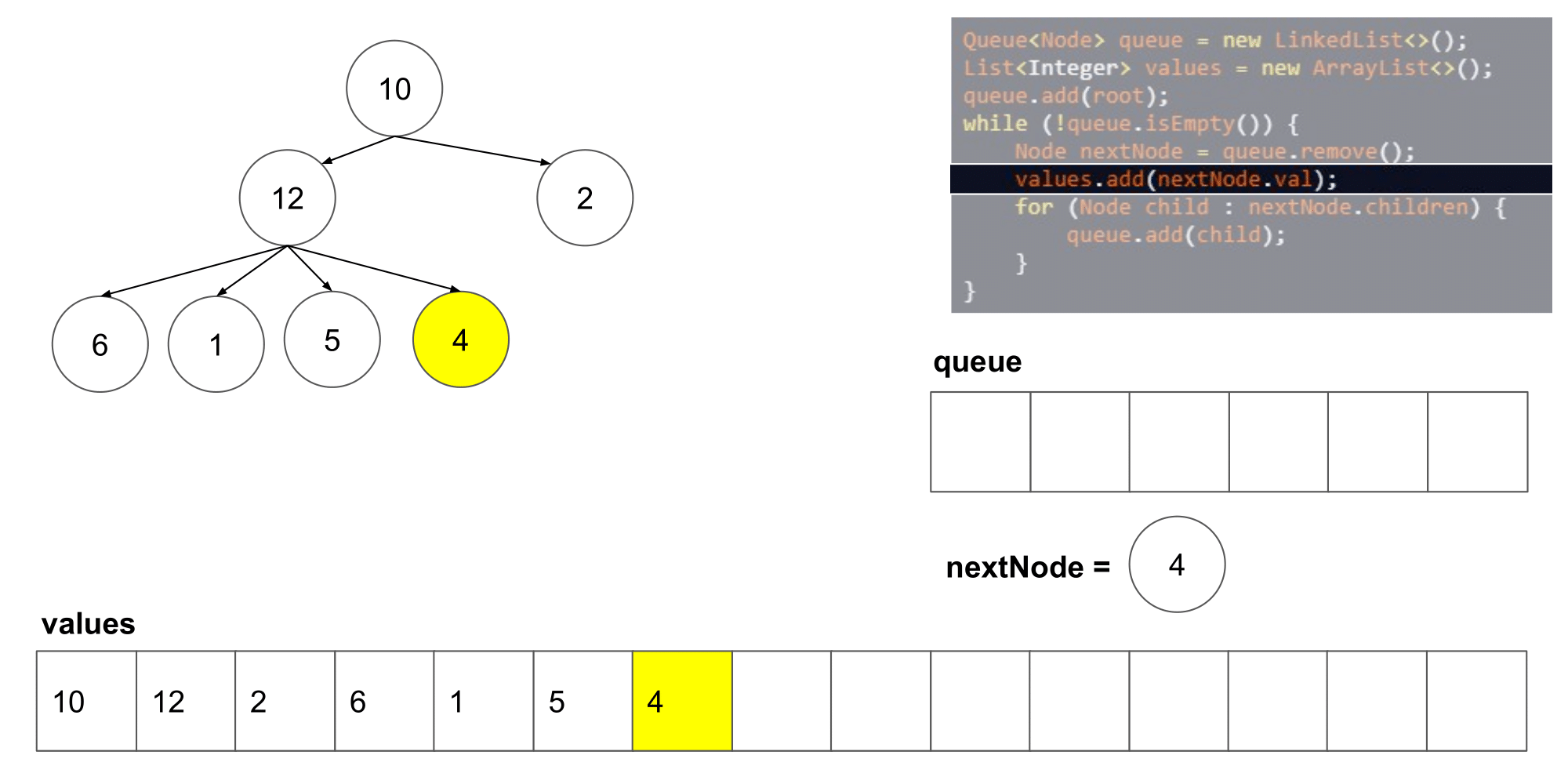
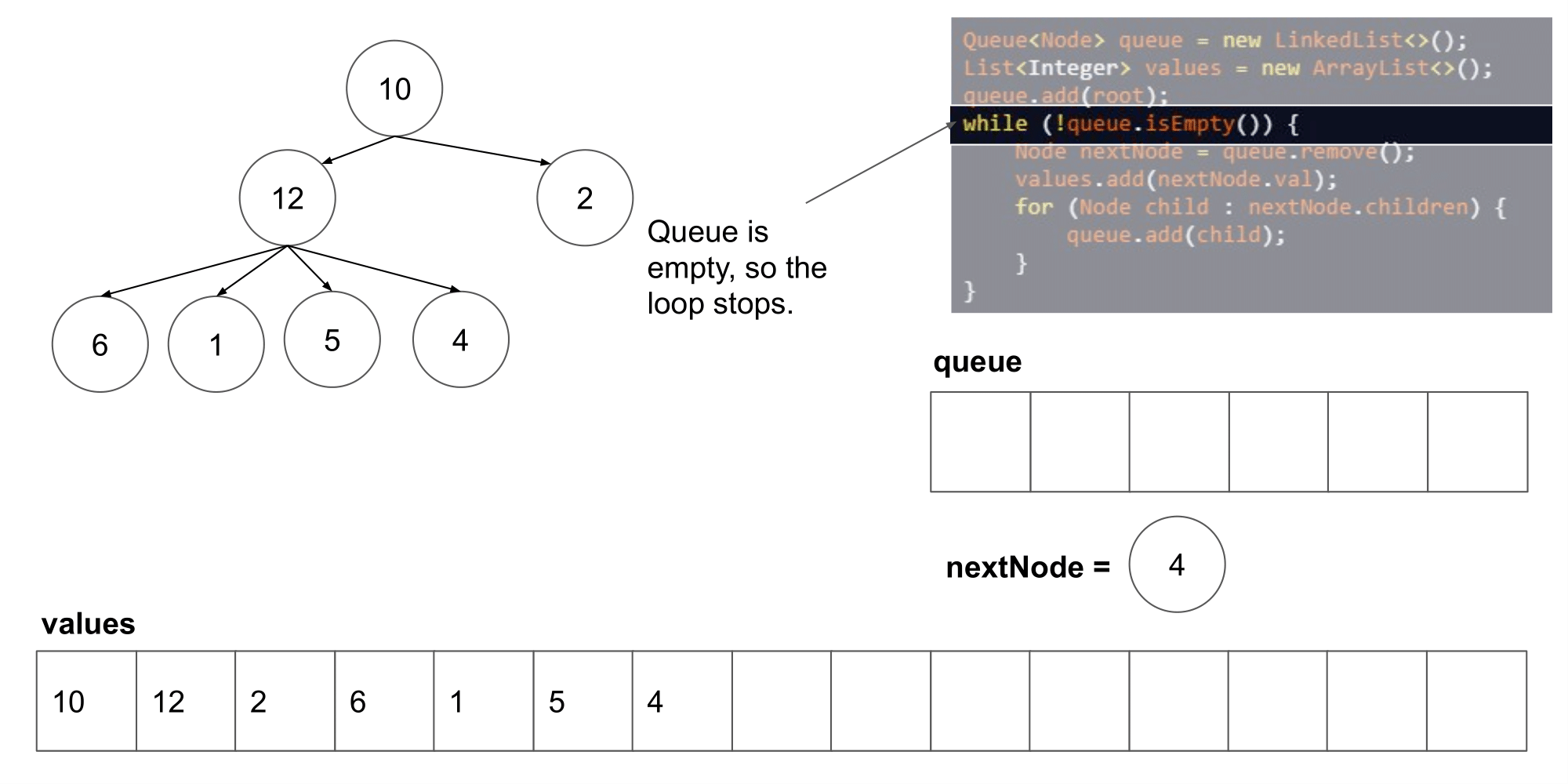
-
时间复杂度:O(n),n 指的是结点的数量;空间复杂度:O(n)。
2.2.2 该题的伪代码
vector<vector<int>> levelOrder(Node* root)
{
创建vector容器,int型变量ans
if (根结点不存在)
返回 ans
创建Node*型队列q
根结点入队q
while (队q不为空)
{
创建int型vector容器tmp
size为队列q的大小
while (size逐渐减小)
{
node存储q的队首元素
for (i = 0 to i < node的孩子长度,i++)
{
将当前结点的孩子依次入队
}
tmp尾部插入node的val,数据计入答案
当前结点已遍历,出队
}
ans尾部插入tmp
}
返回ans
}
2.2.3 运行结果

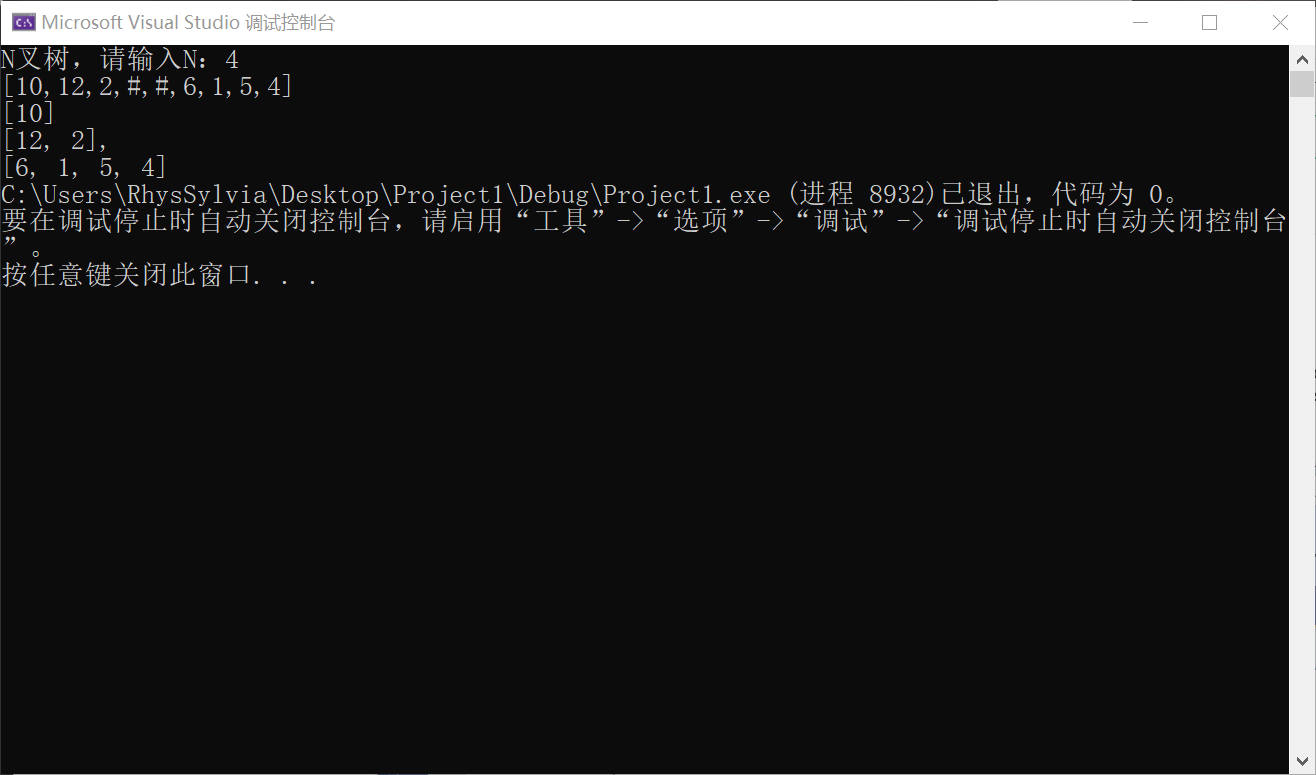
2.2.4 分析该题目解题优势及难点
- 这道题可以仿照二叉树的层次遍历来进行运算,在理解题目上比较容易
- 在这道题中认识到了vector容器,它是一个能够存放任意类型的动态数组,还能够增加和压缩数据,可以在平时也能多去运用
- 附:vector函数相关资料:
2.3 二叉树最大宽度
- 题目
给定一个二叉树,编写一个函数来获取这个树的最大宽度。树的宽度是所有层中的最大宽度。这个二叉树与满二叉树(full binary tree)结构相同,但一些节点为空。
每一层的宽度被定义为两个端点(该层最左和最右的非空节点,两端点间的null节点也计入长度)之间的长度。
示例 1:
输入:
1
/ \
3 2
/ \ \
5 3 9
输出: 4
解释: 最大值出现在树的第 3 层,宽度为 4 (5,3,null,9)。
示例 2:
输入:
1
/
3
/ \
5 3
输出: 2
解释: 最大值出现在树的第 3 层,宽度为 2 (5,3)。
示例 3:
输入:
1
/ \
3 2
/
5
输出: 2
解释: 最大值出现在树的第 2 层,宽度为 2 (3,2)。
示例 4:
输入:
1
/ \
3 2
/ \
5 9
/ \
6 7
输出: 8
解释: 最大值出现在树的第 4 层,宽度为 8 (6,null,null,null,null,null,null,7)。
注意: 答案在32位有符号整数的表示范围内。
- 代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
// i
// 2i 2i+1
class Solution {
public:
typedef struct node{
TreeNode* p;
double num; // 编号
}node;
int widthOfBinaryTree(TreeNode* root) {
queue<node> q;
q.push({root, 1});
double nowlen = 1;
while(q.size()) {
double len = q.size();
double rmin = DBL_MAX, rmax = 0;
for (double i = 1; i <= len; i++) {
auto t = q.front();
q.pop();
auto point = t.p;
auto number = t.num;
if (point->left) {
rmin = min(rmin, 2 * number);
rmax = max(rmax, 2 * number);
q.push({point->left, 2 * number});
}
if (point->right) {
rmin = min(rmin, 2 * number + 1);
rmax = max(rmax, 2 * number + 1);
q.push({point->right, 2 * number + 1});
}
}
nowlen = max((double)((int)(rmax - rmin) + 1), nowlen);
}
return (int)nowlen;
}
};
2.3.1 该题的设计思路
- 我们需要将给定树中的每个节点都访问一遍,这道题中的思路是:首先给所有节点标号,根节点为0,左子节点编号 = 父节点编号 * 2,右子节点编号 = 父节点编号 * 2 + 1,编号和节点一起入队列,按层遍历,每层的宽度 = 队列末尾节点对应编号 - 队列开头节点对应编号 + 1,在每一次产生下一层之前,更新最大宽度
- 这道题时间复杂度和空间复杂度都为O(n)
2.3.2 该题的伪代码
int widthOfBinaryTree(TreeNode* root)
{
创建node型队列q
入队根结点
创建double型变量nowlen记录当前长度,初始化为1
while (q.size())
{
len记录q.size()
rmin,rmax记录最左端和最右端
for (i = 1 to i <= len,i++)
{
t记录队首元素
出队
number记录t.num
if (当前结点有左孩子)
{
rmin变为min(rmin, 2 * number)的值
rmax变为max(rmax, 2 * number)的值
入队{ point->left, 2 * number }
}
if (当前结点有右孩子)
{
rmin变为min(rmin, 2 * number + 1)的值
rmax变为max(rmax, 2 * number + 1)的值
入队{ point->right, 2 * number + 1 }
}
}
nowlen为rmax - rmin + 1
}
返回 int型nowlen
}
2.3.3 运行结果
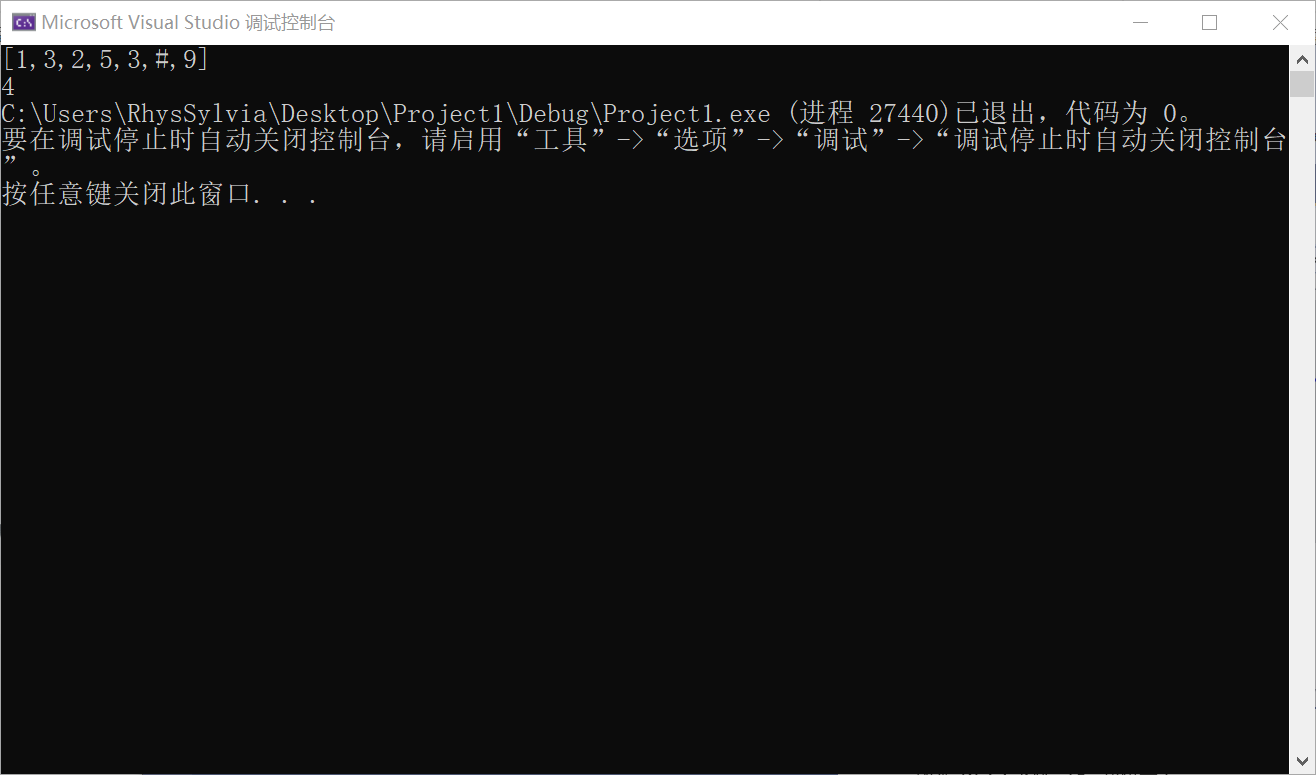

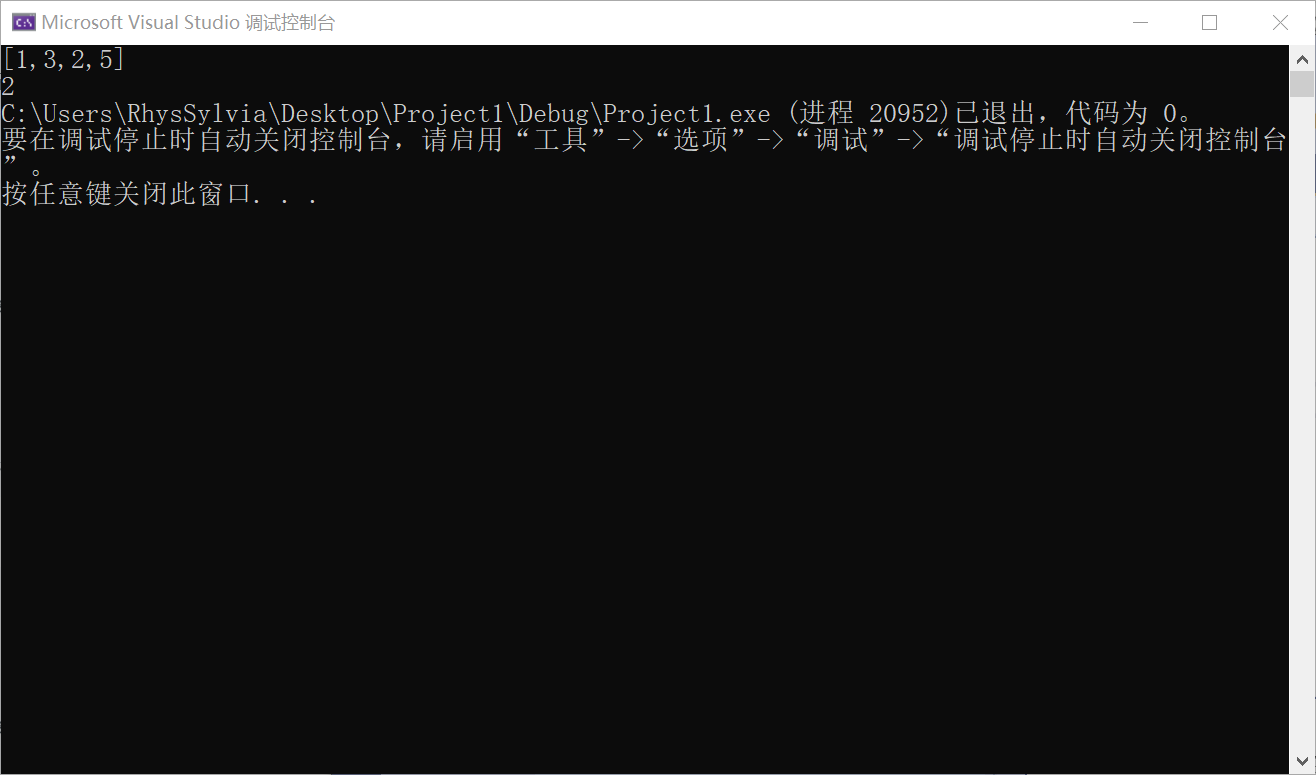

2.3.4 分析该题目解题优势及难点
- 该题用到了层序遍历,需要记录每个节点的索引,当每层遍历完成后再计算下一层的最大宽度
- 可以使用左右孩子和其父亲2i和2i+1的关系来存储结点和计算
- 为了避免溢出数据需要使用double型来存储,但是最后还要用int型输出
2.4 求根到叶子节点数字之和
- 题目
给定一个二叉树,它的每个结点都存放一个 0-9 的数字,每条从根到叶子节点的路径都代表一个数字。
例如,从根到叶子节点路径 1->2->3 代表数字 123。
计算从根到叶子节点生成的所有数字之和。
说明: 叶子节点是指没有子节点的节点。
示例 1:
输入: [1,2,3]
1
/ \
2 3
输出: 25
解释:
从根到叶子节点路径 1->2 代表数字 12.
从根到叶子节点路径 1->3 代表数字 13.
因此,数字总和 = 12 + 13 = 25.
示例 2:
输入: [4,9,0,5,1]
4
/ \
9 0
/ \
5 1
输出: 1026
解释:
从根到叶子节点路径 4->9->5 代表数字 495.
从根到叶子节点路径 4->9->1 代表数字 491.
从根到叶子节点路径 4->0 代表数字 40.
因此,数字总和 = 495 + 491 + 40 = 1026.
- 代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
int result = 0;
public int sumNumbers(TreeNode root) {
//为空时直接返回0
if (root == null) return 0;
dfs(root,0);
return result;
}
public void dfs(TreeNode node,int current){
//加上该节点的val
current += node.val;
//判断是否加入到结果中
if (node.left == null && node.right == null) result += current;
//左子树
if (node.left != null) dfs(node.left,current*10);
//右子树
if (node.right != null) dfs(node.right,current*10);
}
}
2.4.1 该题的设计思路
- 举例说明:从根到叶子节点路径 4->9->5 代表数字 495.从根到叶子节点路径 4->9->1 代表数字 491.从根到叶子节点路径 4->0 代表数字 40.因此,数字总和 = 495 + 491 + 40 = 1026.所以需要进行先序遍历 根1->左2->左3 4 * 10 = 40+9 * 10 = 490+5 = 495;根1->左2->右3 4* 10 = 40+9 * 10 = 490+1= 491;根1->右2 4* 10 = 40 +0 = 40;最后相加即可
- 该题的时间复杂度为O(n),空间复杂度为O(1)
2.4.2 该题的伪代码
定义int型result变量存储结果,初始化为0
int sumNumbers(TreeNode root)
{
if (根结点为空) 返回0
不为空,进入dfs函数
返回result的值
}
void dfs(TreeNode node, int current)
{
current加上该结点的值val
if (为叶结点) result加上current的值
if (左孩子不为空) 递归调用dfs函数,current值乘10
if (右孩子不为空) 递归调用dfs函数,current值乘10
}
2.4.3 运行结果
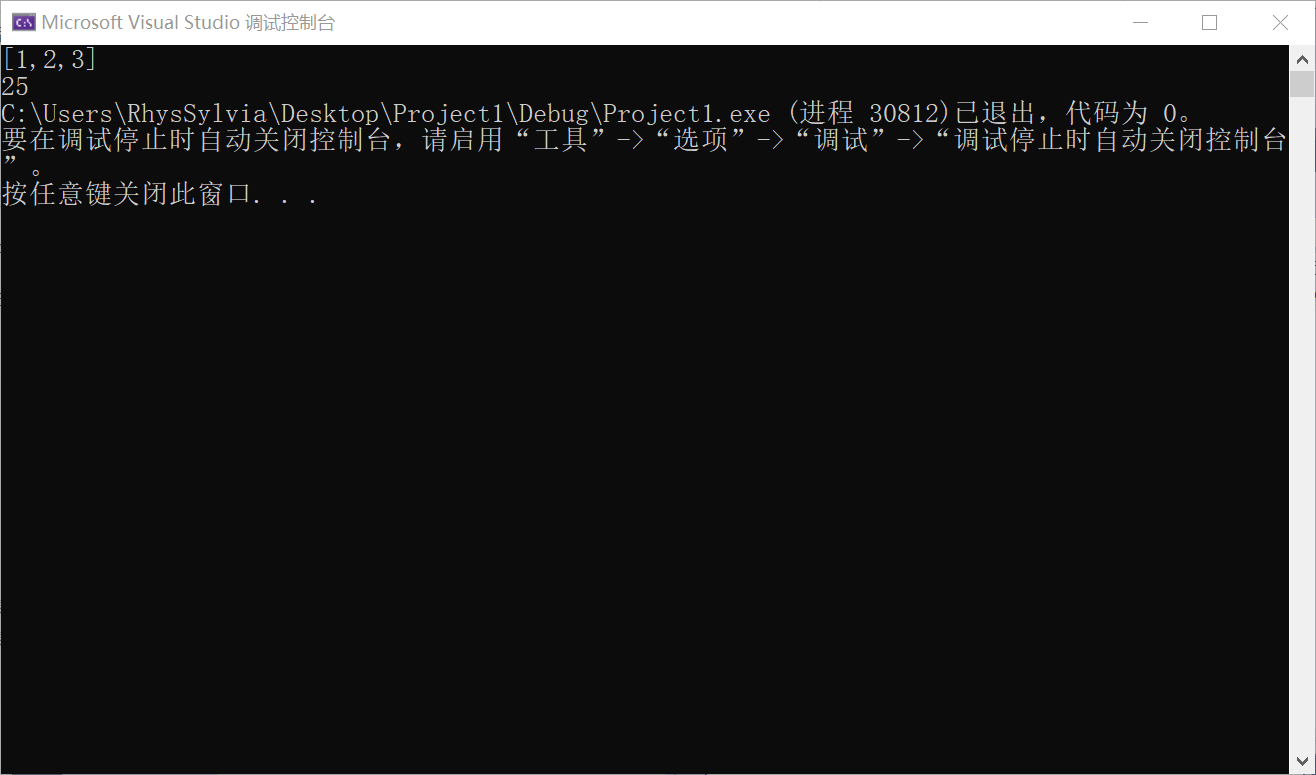
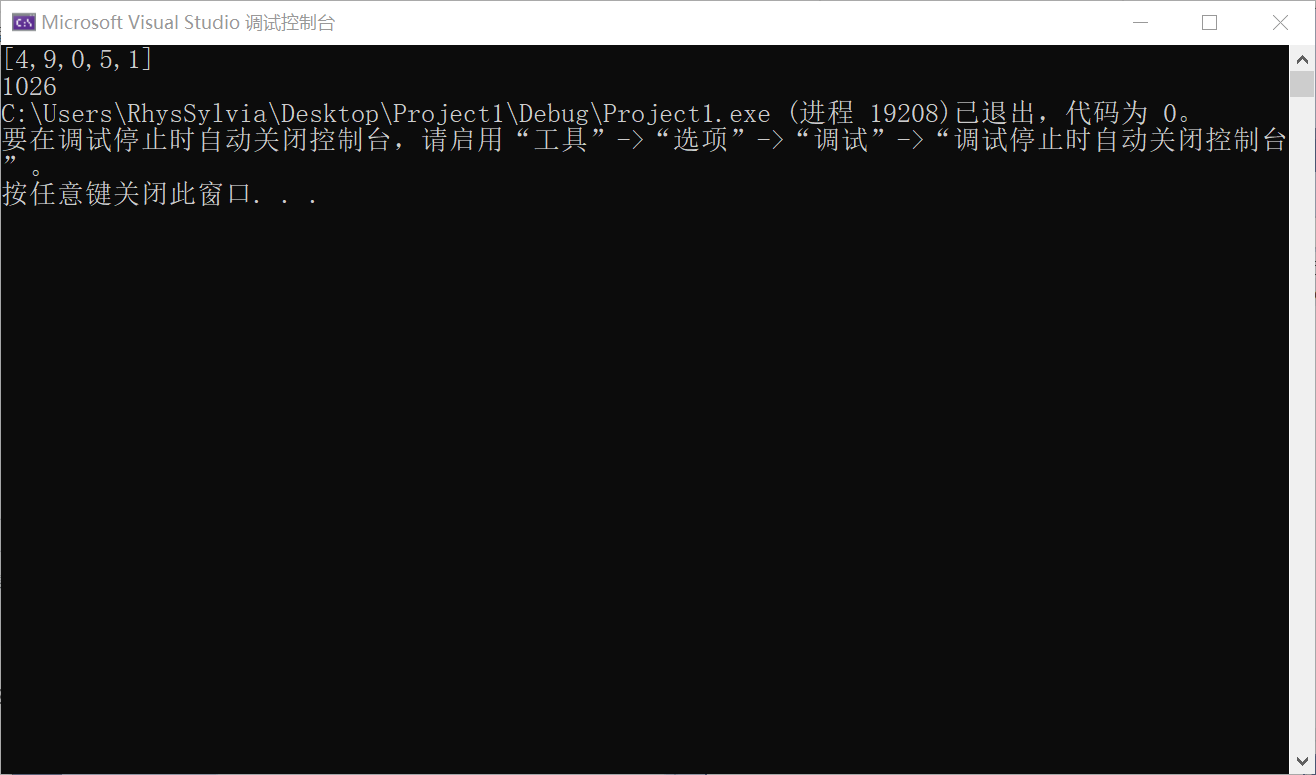
2.4.4 分析该题目解题优势及难点
- 这道题主要思路就是先深度遍历整个树,每遍历一层,值就是当前节点值+10倍之前的值,然后构造一个可传函数值的变量result,当树的左、右节点都为空即是叶结点时返回结果。
- 返回结果时要注意还有根结点为空的情况;递归该结点的孩子时,需要将先前的值乘10
附:阅读代码相关资料
- [ACM题库题解] (https://www.nowcoder.com/ta/acm-solutions?query=&asc=true&order=&page=2)
- [题库 - 力扣 (LeetCode) - 树] (https://leetcode-cn.com/tag/tree/)

