洛城
DS01-线性表

目录

0. PTA得分截图

1. 本周学习总结

1.1 总结线性表内容

1.顺序表结构体定义


#define MaxSize 100
typedef int ElemType;//ElemType类型实际上是int 
typedef struct 
{	ElemType data[MaxSize];//存放顺序表元素
   	int length ;//存放顺序表的长度
} List;	
typedef List *SqList;

2.顺序表插入


void InsertSqList(SqList& L, int x)//在有序表L中插入x
{
	int i;
	int j;

	i = j = 0;

	for (i = 0; i<L->length && x>L->data[i]; i++);//利用空循环，在L中找到比x大的第一个数，然后就找到了应该插入的节点i

	for (j = L->length; j > i; j--)//将i后面的数据，倒序往后移一位，空出i处的内存
	{
		L->data[j] = L->data[j - 1];
	}

	L->length++;//有序表长度加1
	L->data[i] = x;//在插入位置存入x
}

3.顺序表删除


bool ListDelete(SqList& L, int i, ElemType& e)//删除第i个元素
{
    int j = 0;

    if (i<1 || i>L->length)//如果删除位置不合法，返回false
    {
        return false;
    }

    i--;//将顺序表逻辑序号转化为物理序号，因为下标以0开始

    e = L->data[i];//存储要删除的数据

    for (j = i; j < L->length - 1; j++)//要删除的数据的后面依次往前挪
    {
        L->data[j] = L->data[j + 1];
    }

    L->length--;//顺序表长度减1

    return true;
}
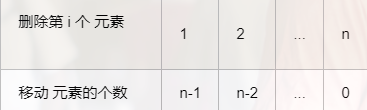
  • Ps：删除元素,时间复杂度为O(n)：
    删除第i个元素，则需要移动n-i个数据元素，即需要移动第i+ 1到第n个元素。通过均值的计算方法可以算出均值为:(n-1)/2，所以时间复杂度为O(n)

void DelSameNode(List& L)//删除顺序表重复元素
{
	int i;
	int j;
	int k;

	i = j = k = 0;

	for (i = 0; i < L->length - 1; i++)//将顺序表遍历
	{
		for (j = i + 1; j < L->length; j++)
		{
			if (L->data[i] == L->data[j])//如果相等，则将后续数据依次往前挪
			{
				for (k = j; k < L->length - 1; k++)
				{
					L->data[k] = L->data[k + 1];
				}

				L->length--;//顺序表长度减1
				j--;//长度减1后，如果少了j--，就会把链表中减少重复后改变的略过，导致有元素没有参与
			}
		}
	}
}




void DelNode(SqList& L, int min, int max)//顺序表删除区间元素
{
	int i = 0;
	int j = 0;

	for (i = 0; i < L->length; i++)//遍历
	{
		if (L->data[i] > max || L->data[i] < min)//如果不在区间内，则将其存入新的顺序表中
		{
			L->data[j] = L->data[i];
			j++;
		}
	}

	L->length = j;//长度改变
}

4.链表结构体定义


typedef struct LNode {
    ElemType data;//数据域
    struct LNode* next;//指针域
}LNode, * LinkList;

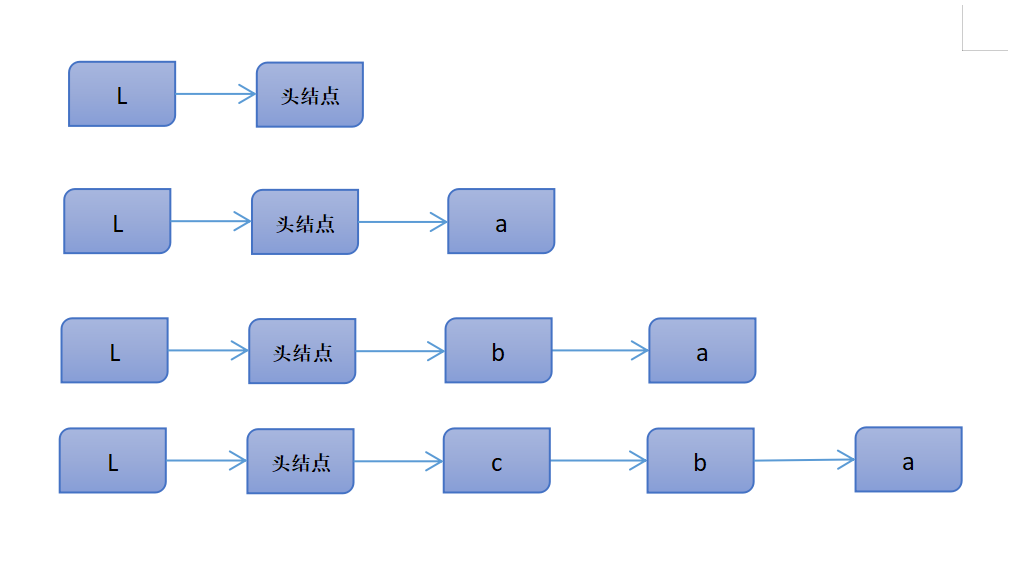
5.头插法建链表


void CreateListF(LinkList& L, int n)//头插法建链表，L表示带头结点链表，n表示数据元素个数
{
	int i;
	LinkList nodePtr;

	L = new LNode;
	L->next = NULL;

	for (i = 0; i < n; i++)
	{
		nodePtr = new LNode;//每个节点都动态申请
		cin >> nodePtr->data;
		nodePtr->next = L->next;
		L->next = nodePtr;
	}
}


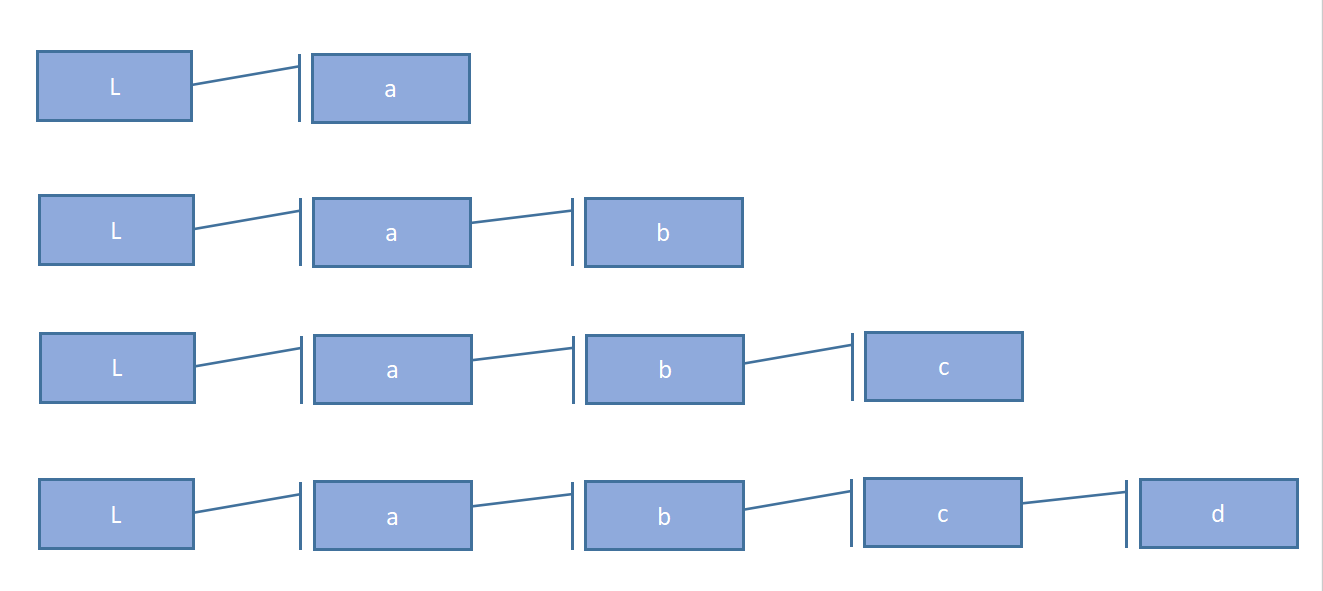
6.尾插法建链表


void CreateListR(LinkList& L, int n)//尾插法建链表，L表示带头结点链表，n表示数据元素个数
{
	int i;
	LinkList q = new LNode;
	LinkList p = new LNode;

	L = new LNode;
	L->next = NULL;
	q = L;

	for (i = 0; i < n; i++)
	{
		p = new LNode;
		cin >> p->data;
		q->next = p;//q的后继为新的元素
		q = p;//q后移至下一位
	}

	q->next = NULL;

}

7.链表插入


void ListInsert(LinkList& L, ElemType e)//有序链表插入元素e
{
    LinkList p;
    LinkList node;

    p = new LNode;
    p = L;
    node = new LNode;

    while (1) 
    {
        if (p != NULL && p->next != NULL) 
        {
            if (e >= p->data && e <= p->next->data)//找到可以插入的前和后
            {
                node->data = e;
                node->next = p->next;
                p->next = node;
                return;
            }
            p = p->next;
        }
        else
        {
            break;
        }
            
    }

    //插入的数在最后
    node->data = e;
    p->next = node;
    p = p->next;
    p->next = NULL;

    return;
}

8.链表删除


void ListDelete(LinkList& L, ElemType e)//链表删除元素e
{
    LinkList p;

    p = new LNode;
    p = L;

    if (p->next == NULL)
    {
        return;
    }
        
    while (1) 
    {
        if (p != NULL && p->next != NULL) 
        {
            if (e == p->next->data)//找到e，跳过
            {
                p->next = p->next->next;
                return;
            }
        }
        
        if (p == NULL)
        {
            break;
        }
           
        p = p->next;

    }

    cout << e << "找不到！" << endl;//循环结束，找不到e
}

9.有序单链表数据插入


void ListInsert(LinkNode*& L，ElemType e)
{
    LinkNode* pre = L, * p;

    while (pre->next != NULL && pre->next->data < e)
    {
        pre = pre->next;//查找插入结点的前驱结点*pre
    }        

    p = new LinkNode;
    p->data = e;//创建存放e的数据结点*p
    p->next = pre->next;//在*pre结点之后插入*p结点
    pre->next = p;

}

10.有序单链表数据删除


void DeleteList(LinkNode*& L, int i, ElemType& e)
{
	int j = 0;
	LinkNode* p = L, * q;//p指向头结点，j为头结点的序号，即j为0

	if (i <= 0)//i值不合逻辑
	{
		return false;
	}

	while (j < i - 1 && p != NULL)//查找第i-1个结点
	{
		j++;
		p = p->next;
	}

	if (p == NULL)//如果未找到i-1个结点，返回false
	{
		return false;
	}
	else//找到第i-1个结点p
	{
		q = p->next;//q指向第i个结点

		if (q == NULL)//若不存在第i个结点，返回false
		{
			return false;
		}

		e = q->data;
		p->next = q->next;//从单链表中删除q结点
		free(q);//释放q结点

		return true;//返回true，成功删除第i个结点
	}


}

11.有序表合并(二路归并算法)


void UnionList(SqList* LA，SqList* LB，SqList*& LC)
{
	int i, j, k;//i、j分别为LA、LB的下标，k为LC中元素个数
	
	i = j = k = 0;
	LC = new SqList;//建立有序顺序表LC

	while (i < LA->length && j < LB->length)//LA、LB不为空时
	{
		if (LA->data[i] < LB->data[j])
		{
			LC->data[k] = LA->data[i];
			i++; k++;
		}
		else//LA->data[i]>=LB->data[j]
		{
			LC->data[k] = LB->data[j];
			j++; k++;
		}
	}

	while (i < LA->length)//LA尚未扫描完，将其余元素插入LC中
	{
		LC->data[k] = LA->data[i];
		i++; k++;
	}

	while (j < LB->length)//LB尚未扫描完，将其余元素插入LC中
	{
		LC->data[k] = LB->data[j];
		j++; k++;
	}

	LC->length = k;//LC的长度即为k
}

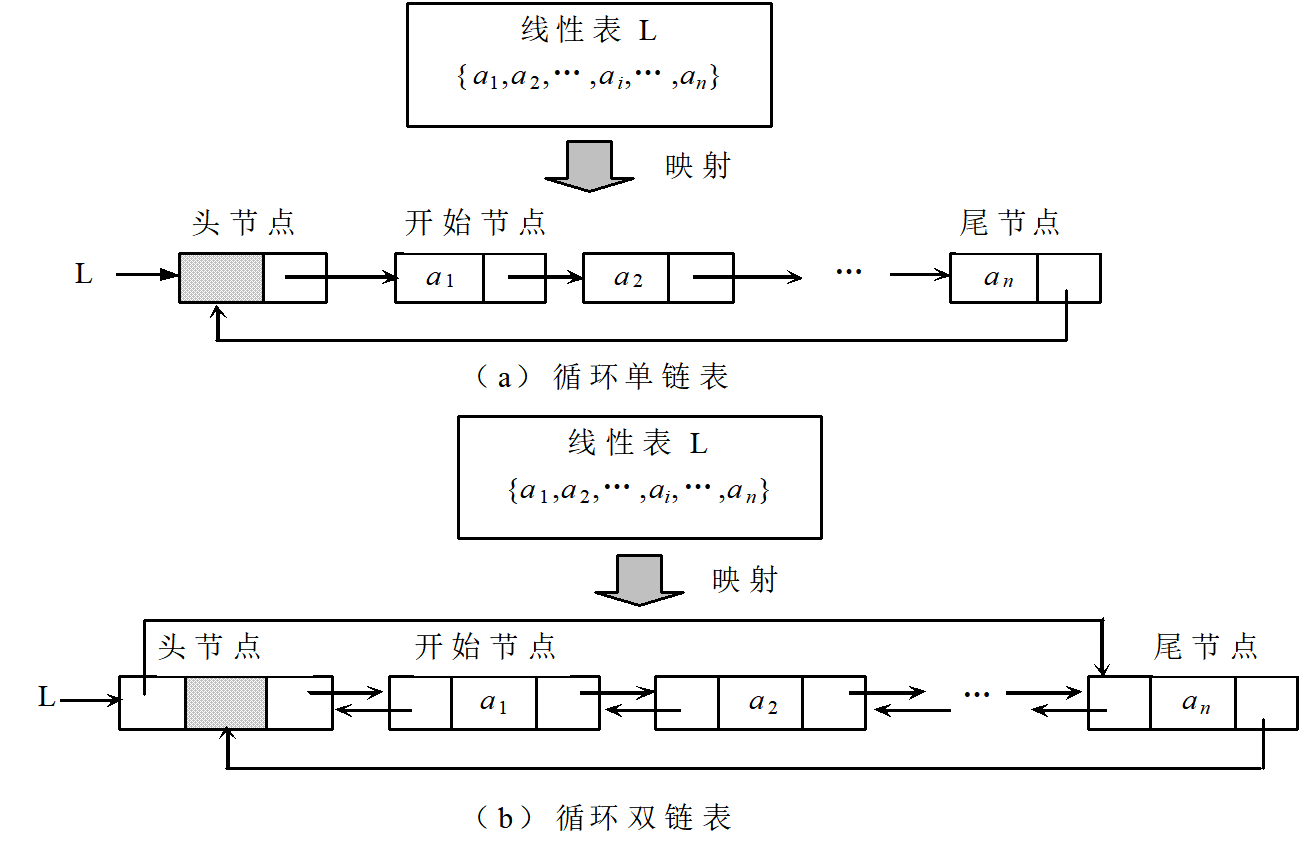
12.循环链表特点


1)循环单链表特点：
①从循环链表中的任何一个结点的位置都可以找到其他所有结点
②循环链表中没有明显的尾端，带头结点时循环条件为：p->next!=L，不带头结点时循环条件为：p!=L

2)循环双链表特点：
①链表中没有空指针域
②p所指结点为尾结点的条件：p->next==L
③一步操作即L->prior可以找到尾结点

13.双链表结构特点


1>双链表每个节点有2个指针域，一个指向后继节点，一个指向前驱节点

2>定义类型：
typedef struct DNode//声明双链表节点类型
{	ElemType data;
        struct DNode *prior;//指向前驱节点
	struct DNode *next;//指向后继节点
} DLinkList;

3>双链表优点：
①从任一结点出发可以快速找到其前驱结点和后继结点；
②从任一结点出发可以访问其他结点。

14.头插法建立双链表


void CreateListF(DLinkNode*& L，ElemType a[]，int n)//由含有n个元素的数组a创建带头结点的双链表L
{
    DLinkNode* s;
    int i = 0;

    L = (DLinkNode*)malloc(sizeof(DLinkNode));//创建头结点
    L->prior = L->next = NULL;//前后指针域置为NULL

    for (i = 0; i < n; i++)//循环建立数据结点
    {
        s = (DLinkNode*)malloc(sizeof(DLinkNode));
        s->data = a[i];//创建数据结点*s
        s->next = L->next;//将*s插入到头结点之后

        if (L->next != NULL)//若L存在数据结点，修改前驱指针
        {
            L->next->prior = s;
        }
            
        L->next = s;
        s->prior = L;

    }
}

15.尾插法建立双链表


void CreateListR(DLinkNode*& L，ElemType a[]，int n)//由含有n个元素的数组a创建带头结点的双链表L
{
    DLinkNode* s，* r;
    int i = 0;

    L = (DLinkNode*)malloc(sizeof(DLinkNode));//创建头结点
    L->prior = L->next = NULL;//前后指针域置为NULL
    r = L;//r始终指向尾结点，开始时指向头结点

    for (i = 0; i < n; i++)//循环建立数据结点
    {
        s = (DLinkNode*)malloc(sizeof(DLinkNode));
        s->data = a[i];//创建数据结点*s
        r->next = s;
        s->prior = r;//将*s插入*r之后
        r = s;//r指向尾结点
    }

    r->next = NULL;//尾结点next域置为NULL

}

1.2 对线性表的认识及学习体会


我感觉线性表这方面比较绕，一些的概念不是很明白。
线性表有顺序存储和链式存储之分，在做PTA时，我明显感觉到做顺序存储，也就是利用数组来做的时候，比较好理解一些，如果同样的题，我用链表去做，就很容易把自己绕进去，尤其一些比较细微的地方，比如空间堆栈溢出，然后就一直找不着到底是哪里错误了，而且消耗的时间也很久，基本上一道题需要做好几天，还需要经常去看别的代码，模仿着来一点一点地写。
而且在有关next的内容上，也比较混乱，画图画得最后越来越复杂......看代码时还比较好懂，可以想明白，但到了自己要写的时候就有些无从下手了，所以比较郁闷。
不过老师的课件以及课本上面的内容比较全面，也经常可以问问其他同学，现在基本上是全靠模仿来做题理解，距离理解透彻还有很大差距，不过我一定会多做题的！希望早日把这块弄明白！

2. PTA实验作业

2.1 题目1：6-11 jmu-ds-链表分割 (20分)

该函数实现链表的分割。尾插法建好初始链表L={a1,b1,a2,b2,.....an,bn}。分割2个链表，其中L1和L共享头结点，分割后链表如下：

  • L1:
  • L2:

函数接口定义：


void SplitList(LinkList &L, LinkList &L1, LinkList &L2);

L为原链表，L1和L共享头结点，正序链表，L2为倒序链表

裁判测试程序样例：


#include <iostream>
using namespace std;
typedef int ElemType;
typedef struct LNode  		//定义单链表结点类型
{
	ElemType data;
	struct LNode *next;		//指向后继结点
} LNode, *LinkList;
void CreateListR(LinkList &L, int n);//尾插法建链表
void DispList(LinkList L);//输出链表
void DestroyList(LinkList &L);//销毁链表
void SplitList(LinkList &L, LinkList &L1, LinkList &L2);
int main()
{
	LinkList L,L1,L2;
	int n;
	cin >> n;//输入链表节点个数
	CreateListR(L, n);//尾插法建带头结点链表，细节不表
	SplitList(L, L1, L2);
	DispList(L1);//输出链表，细节不表
	cout << endl;
	DispList(L2);//输出链表，细节不表
	DestroyList(L);//销毁链尾，细节不表
	return 0;
}

/* 请在这里填写答案 */

输入样例：

5
1 2 3 4 5

输出样例：

1 3 5
4 2

2.1.1 代码截图


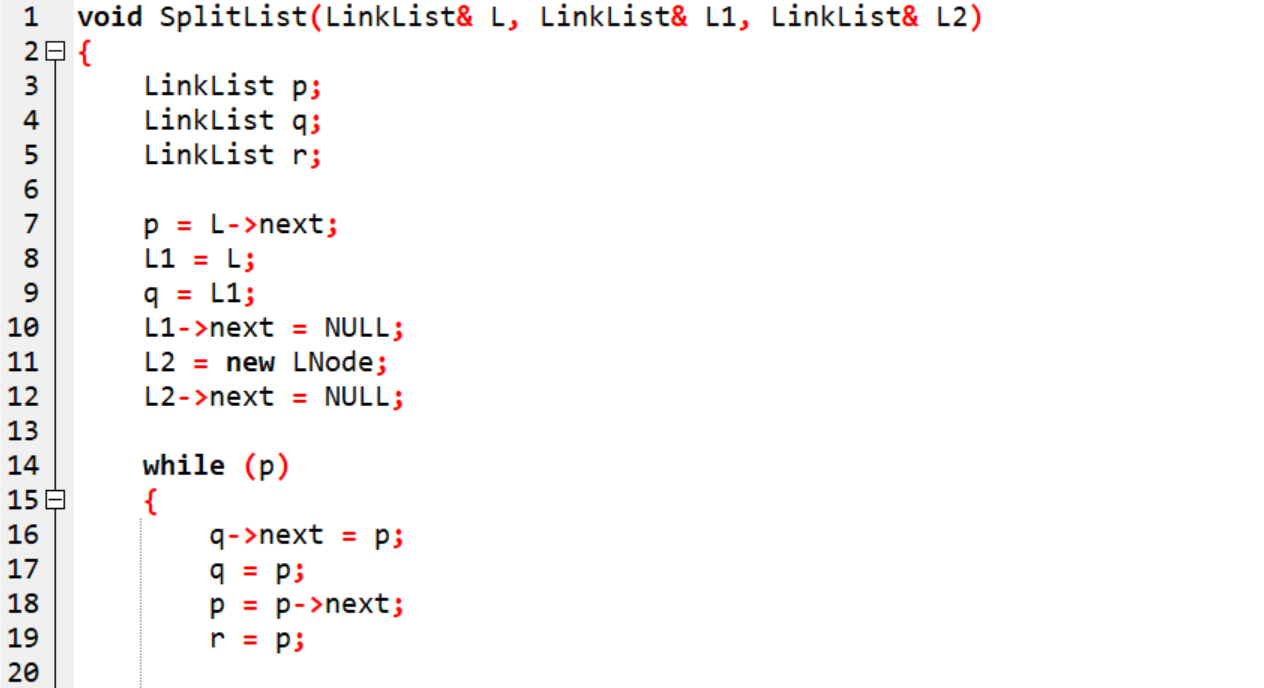
2.1.2 本题PTA提交列表说明

  • 段错误：结点之间的连接有问题，造成堆栈溢出
  • 答案正确：这道题是将初始链表L间隔分割成新的2条链表，但是需要注意L和L1是共享头结点的

2.2 题目2：7-1 两个有序序列的中位数 (25分)

输入样例1:

5
1 3 5 7 9
2 3 4 5 6

输出样例1:

4

输入样例2:

6
-100 -10 1 1 1 1
-50 0 2 3 4 5

输出样例2:

1

2.2.1 代码截图





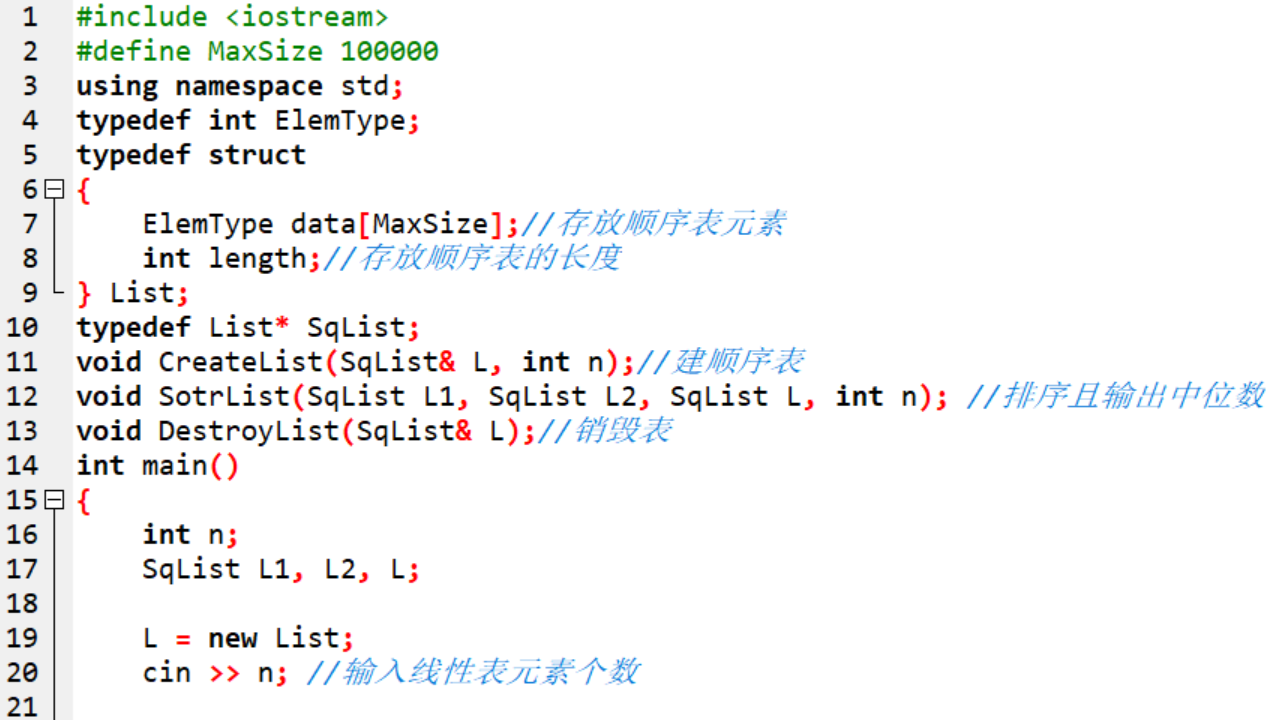
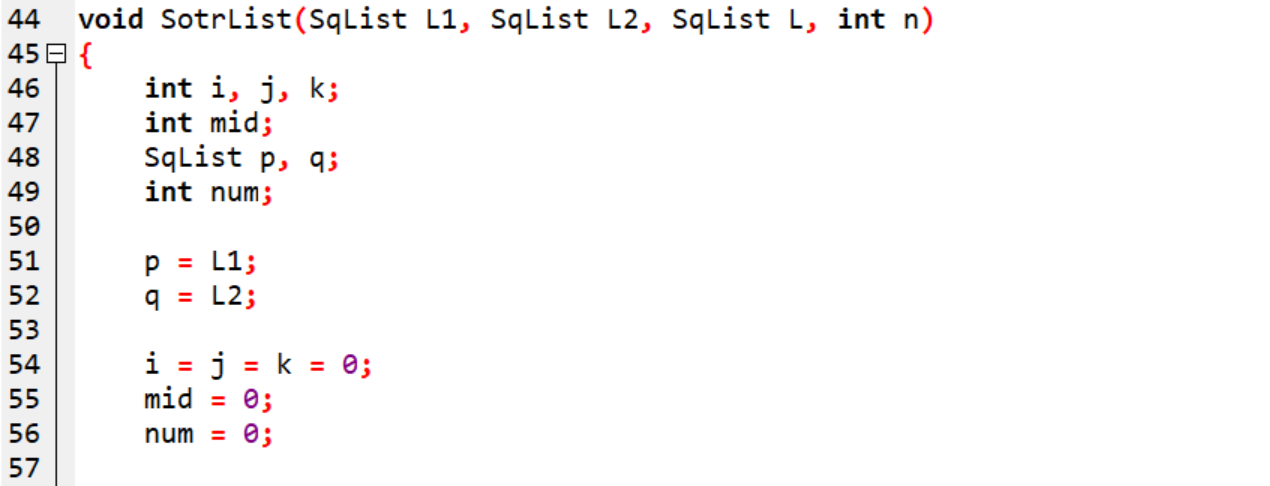
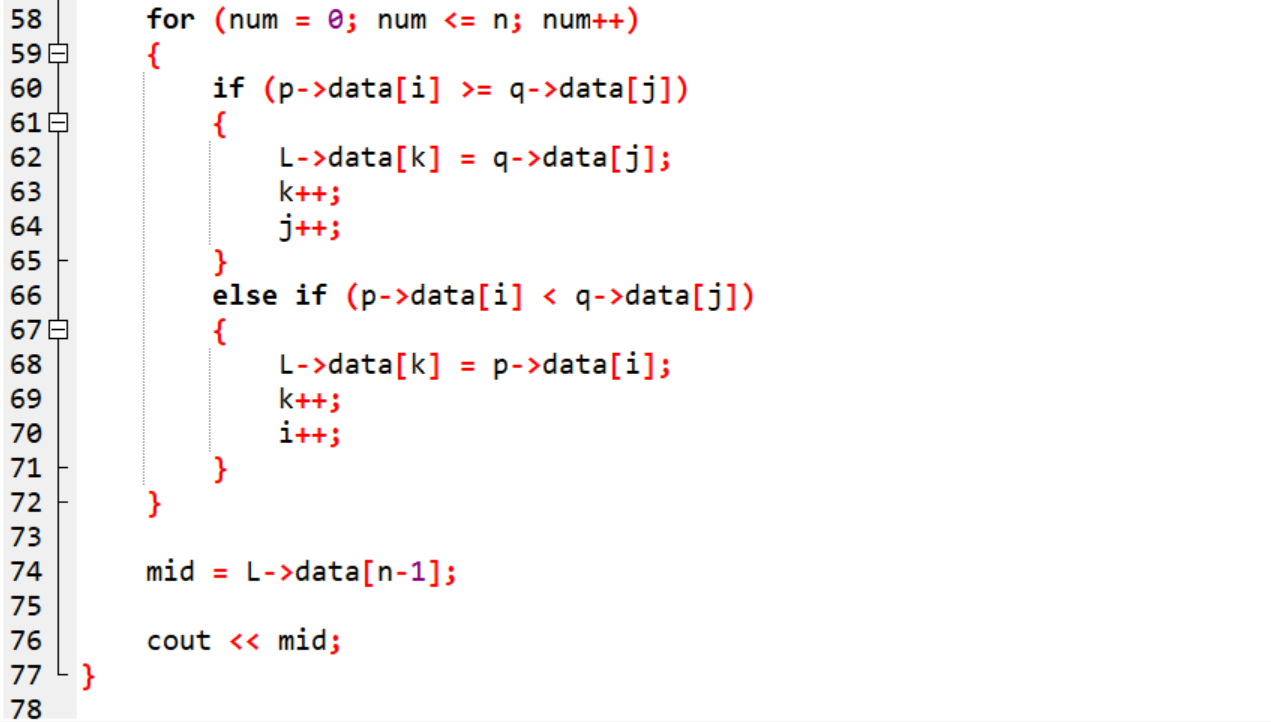
2.2.2 本题PTA提交列表说明

  • 部分正确：刚开始使用链表的方法，但是结点移动时造成错误，只有N最小，即N等于0时的测试点可以通过
  • 段错误：排序排到中间时的存储空间不够，造成堆栈溢出
  • 答案正确：改用顺序表去做，在数据方面的认知可以比较清晰

2.3 题目3：7-2 一元多项式的乘法与加法运算 (20分)

输入样例:

4 3 4 -5 2  6 1  -2 0
3 5 20  -7 4  3 1

输出样例:

15 24 -25 22 30 21 -10 20 -21 8 35 6 -33 5 14 4 -15 3 18 2 -6 1
5 20 -4 4 -5 2 9 1 -2 0

2.3.1 代码截图











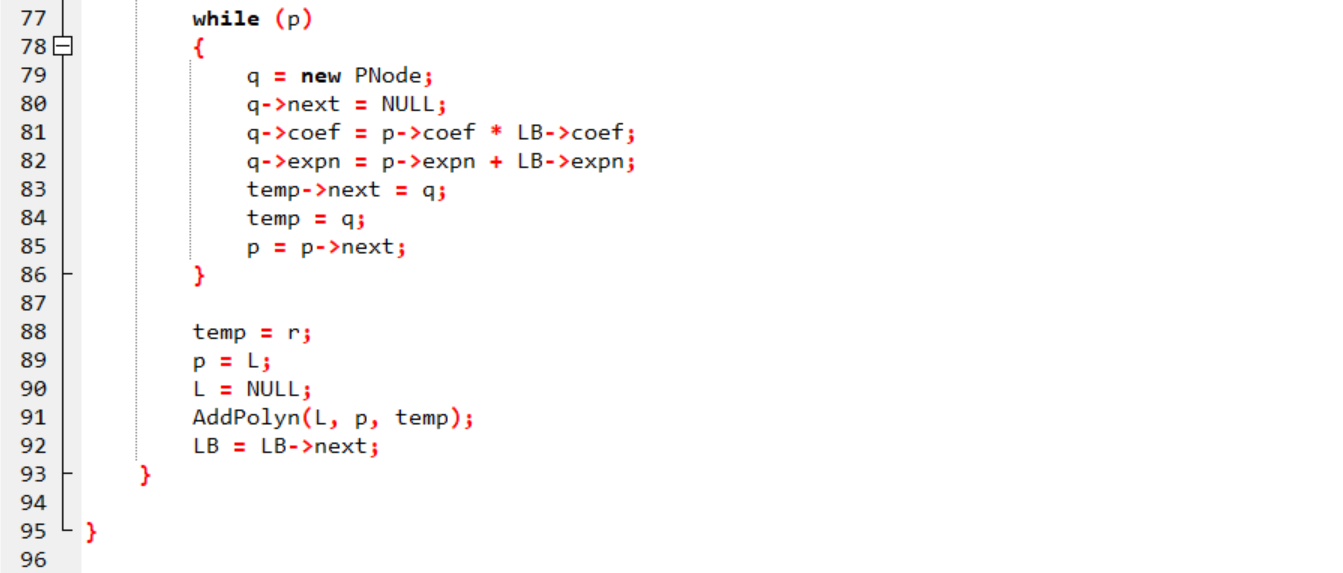
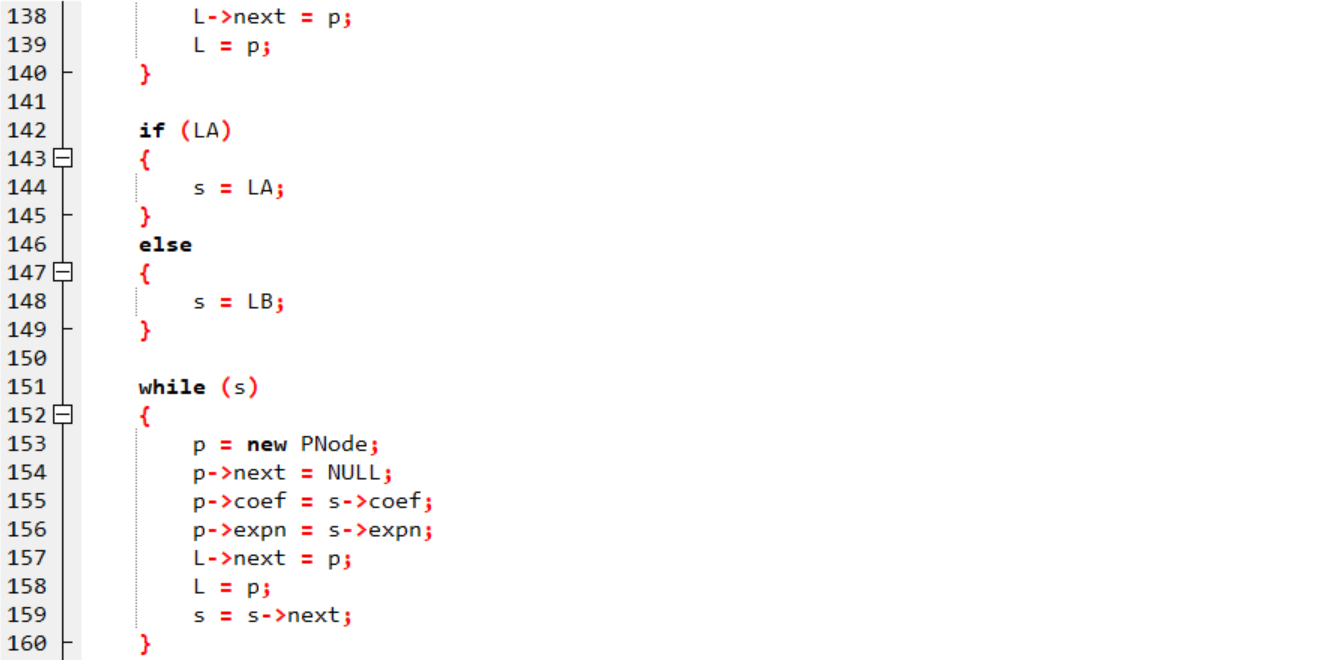
2.3.2 本题PTA提交列表说明

  • 编译错误：暂时没有找到这个错误的原因，vs上说无法解析
  • 段错误：在结点向后传递之后，没有改变先前结点的地址
  • 答案正确：这道题很复杂，但是题意比较好理解，一元多项式的乘法需要将两个多项式的每一项分别相乘，然后再把指数相同的项进行整合；而加法则是把指数相同的项进行相加

3. 阅读代码

3.1 有序链表转换二叉搜索树

3.1.1 题目描述

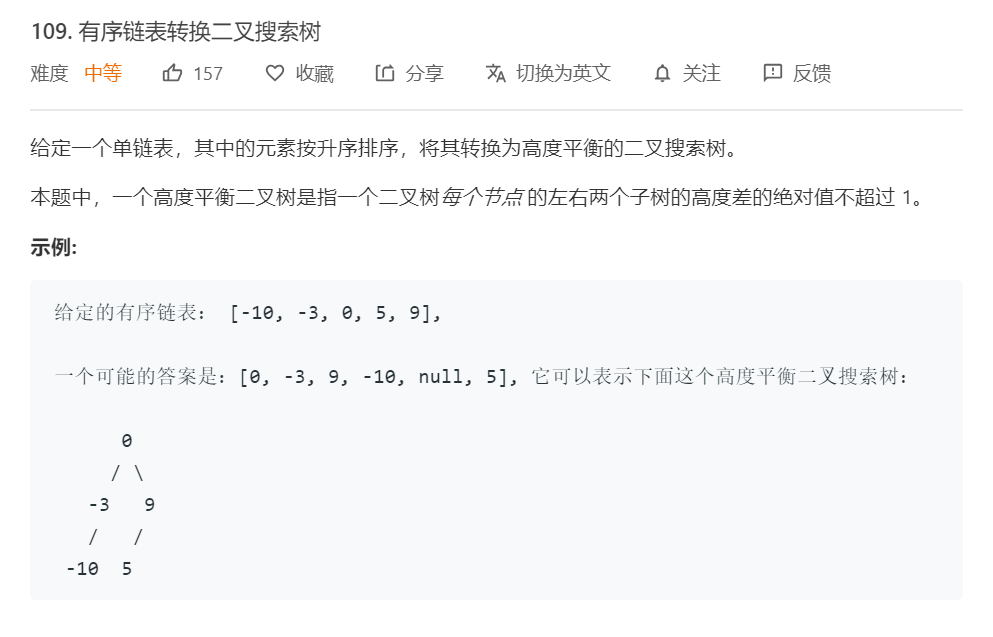
3.1.2 解题代码


/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
 /**
  * Definition for a binary tree node.
  * struct TreeNode {
  *     int val;
  *     TreeNode *left;
  *     TreeNode *right;
  *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
  * };
  */

class Solution {
public:
    ListNode* cuthalf(ListNode* head) {
        if (!head || !head->next) return NULL;
        ListNode* one = head, * two = head;
        ListNode* pre = NULL;
        while (two && two->next) {
            pre = one;
            one = one->next;
            two = two->next;
            two = two->next;
        }
        ListNode* nhead = pre->next;
        pre->next = NULL;
        return nhead;
    }

    TreeNode* sortedListToBST(ListNode* head) {
        return dfs(head);
    }

    TreeNode* dfs(ListNode* head) {
        if (!head) return NULL;
        if (!head->next) {
            return new TreeNode(head->val);
        }
        ListNode* righthalf = cuthalf(head);
        TreeNode* rt = new TreeNode(righthalf->val);
        rt->left = dfs(head);
        rt->right = dfs(righthalf->next);
        return rt;
    }

};

3.1.3 该题的设计思路

  • 作者采用了二分法构造来平衡树，每次选链表中间的节点作为树的根部，中间节点前后的链表分别递归构造两棵平衡树。
  • 例如：[-10,-3,0,5,9]，选择0为根，[-10,-3]为左子树, [5,9]为右子树。
  • 构建好两棵平衡树后，将后一半链表的第一个节点作为根节点，并对左右边的链表，递归构建二叉树。
  • 例如： [-10,-3,0,5,9,10]，要选择5为根，[-10,-3，0]为左子树, [9，10]为右子树。
  • 时间复杂度应该为O(n)，空间复杂度应该为O(1)

3.1.4 该题的伪代码


//将链表拆分成两半，并将后一半返回
cuthalf(head) {
    if (head为空 或 单节点) 返回空;
    one，two指向头结点head;
    pre;
    while (two 且 two的next不为空) {
        前驱pre规定为one;
        one指向one的next;
        two指向two的next的next;
    }
    右子树的头结点right就是pre的next;
    pre的next变为空;
    返回right;
}

dfs(head) {
    if (head为空) 返回空;
    if (head为单节点) 返回节点二叉树;
    
    //分成两半
    右子树right的头结点就是cuthalf(head);
    tree(right.val);
    左子树tree.left是dfs(head);
    右树tree.right是dfs(right.next);
    返回tree;
}

3.1.5 运行结果

  • 我把左子树和右子树分开来输出，但是题目中那个NULL不知道哪里冒出来的

3.1.6 分析该题目解题优势及难点

  • 优势：因为该链表给定的是有序链表，所以选择中间作为根部，可以容易计算，作者使用了一些指针来存储多个头结点，方便且不显凌乱
  • 难点：这道题目要求把给定链表中的数转换为二叉树，但是左支和右支的绝对值之差小于等于1，我不太理解题目给定的答案为什么有一个NULL，这个NULL在二叉树上也没有画出来，给定的链表是5个元素，可能的答案却多出一个来，本来以为是不是分隔开数的，但是后来发现并不是。

3.2 奇偶链表

3.2.1 题目描述


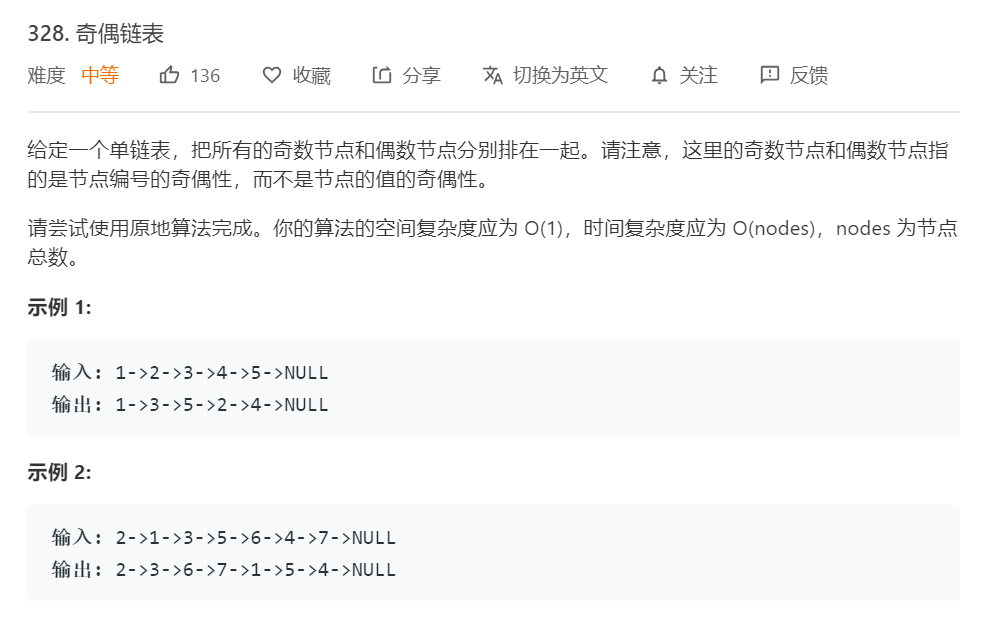
3.2.2 解题代码


public class Solution {
    public ListNode oddEvenList(ListNode head) {
        if (head == null) return null;
        ListNode odd = head, even = head.next, evenHead = even;
        while (even != null && even.next != null) {
            odd.next = even.next;
            odd = odd.next;
            even.next = odd.next;
            even = even.next;
        }
        odd.next = evenHead;
        return head;
    }
}

3.2.3 该题的设计思路

  • 将奇数结点放在一个链表里，偶数结点放在另一个链表里，然后再把偶链表接在奇链表的尾部。
  • 一个LinkedList需要一个头指针和一个尾指针来支持双端操作。我们用变量head和odd保存奇链表的头和尾指针。evenHead和even保存偶链表的头和尾指针。算法会遍历原链表一次并把奇节点放到奇链表里去、偶节点放到偶链表里去。遍历整个链表至少需要一个指针作为迭代器。这里odd指针和even指针不仅仅是尾指针，也可以扮演原链表迭代器的角色。
  • 该题的时间复杂度为O(n)，因为只遍历了一次；空间复杂度为O(1)

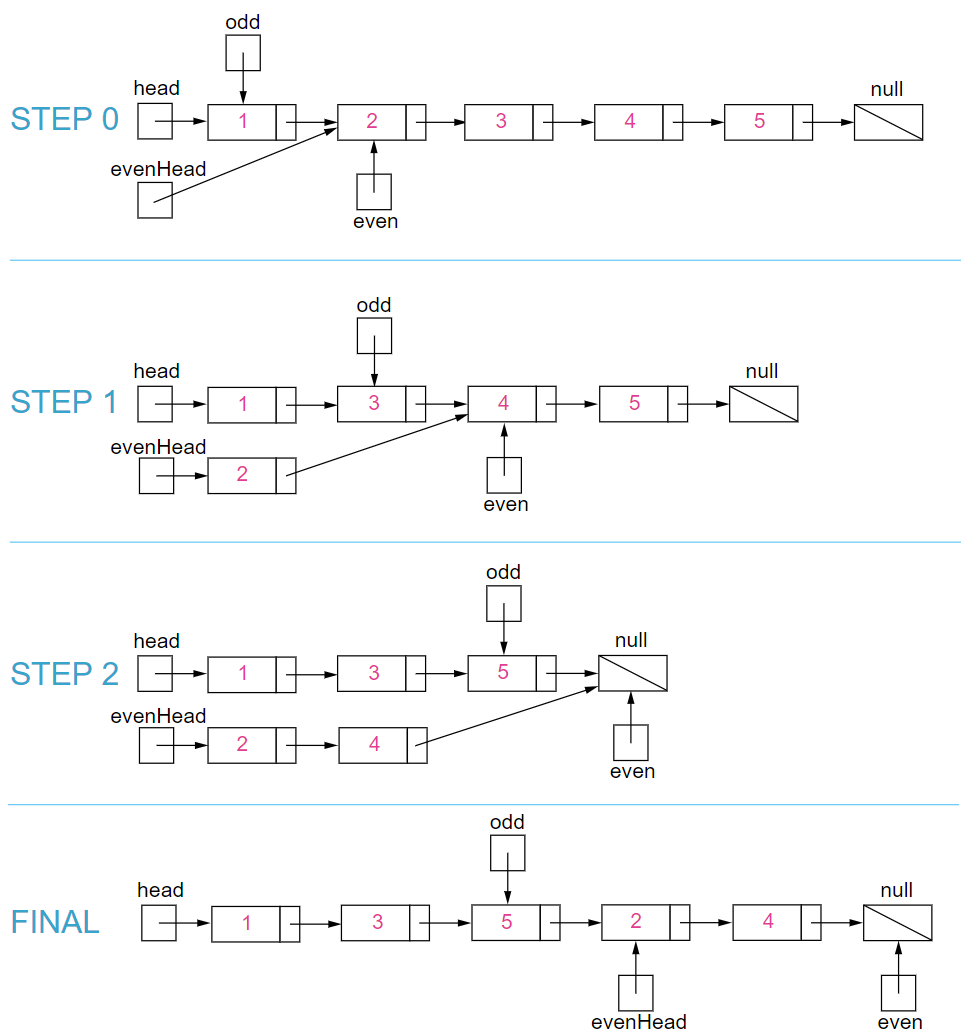
3.2.4 该题的伪代码


public class Solution {
    public ListNode oddEvenList(ListNode head) {
        如果 (head为空) 返回空;
        建立ListNode类型的odd来保存奇数链的头结点head
        建立ListNode类型的even来保存偶数链的头结点head的next, 即偶数头结点evenHead来存储even;

        当 (even和even的next都不为空时) {
            odd的next就是odd的next的next，也就相当于是even的next;
            改变结点后，odd就应该到新的odd结点，也就是odd的next;
            同理，even的next就是even的next的next，也就相当于是odd的next;
            改变结点后，even就应该到新的even结点，也就是even的next;
        }
        odd的next就是even链的头结点，即evenHead，将奇数链和偶数链连接起来;
        返回头结点head;
    }
}

3.2.5 运行结果


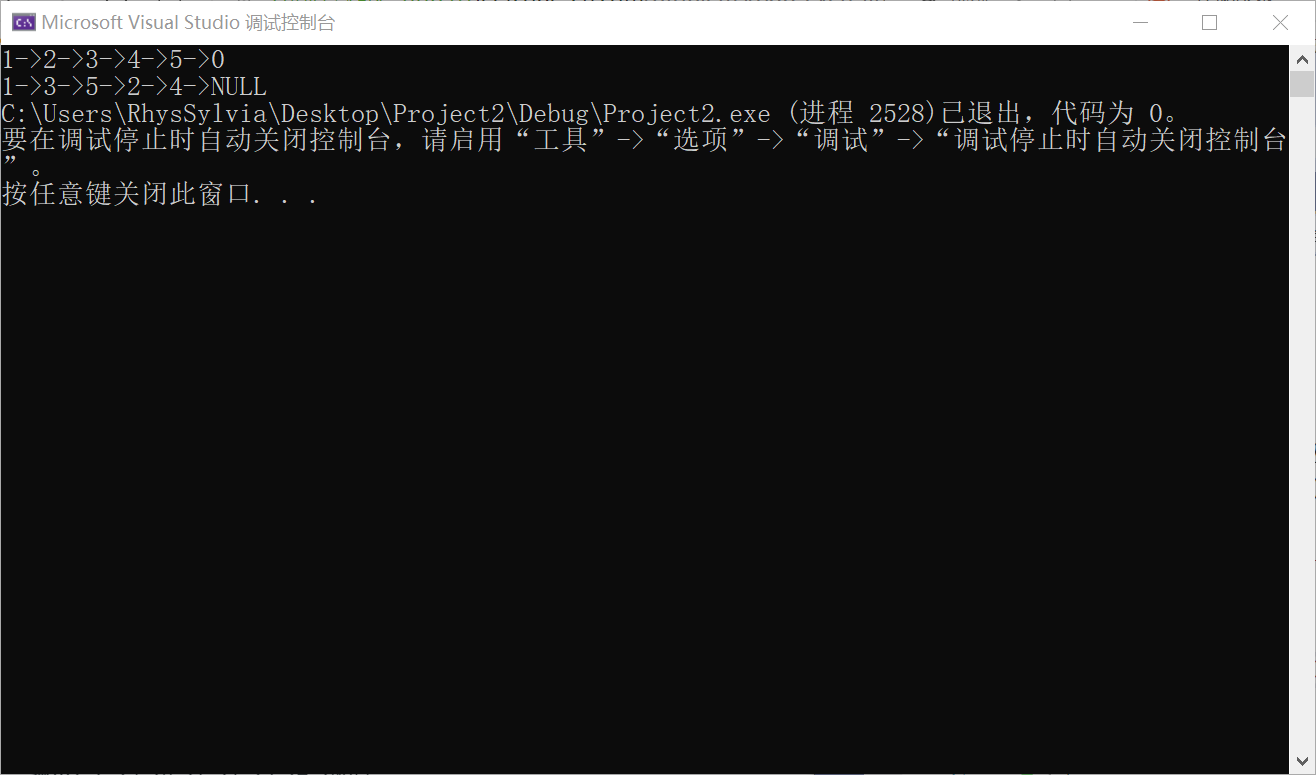
  • 输入链表时最后的NULL时识别不了，不知道怎么修改，所以我只能改成了0

3.2.6 分析该题目解题优势及难点

  • 优势：这道题相当于把一个链表先间隔分成两个链表，然后再把两个链表像接火车一样接在一起，比较好理解
  • 难点：容易将题目分析成为把奇数和偶数分开，所以审题需要认真

附：阅读代码相关资料

posted on 2020-03-08 13:30  R°  阅读(492)  评论(2)  编辑  收藏  举报

Copyright © 2024 R°
Powered by .NET 8.0 on Kubernetes Powered By博客园
/*
*/