之前我们介绍了多元线性回归的原理, 又通过一个案例对多元线性回归模型进一步了解, 其中谈到自变量之间存在高度相关, 容易产生多重共线性问题, 对于多重共线性问题的解决方法有: 删除自变量, 改变数据形式, 添加正则化项, 逐步回归, 主成分分析等. 今天我们来看看其中的添加正则化项.
添加正则化项, 是指在损失函数上添加正则化项, 而正则化项可分为两种: 一种是L1正则化项, 另一种是L2正则化. 我们把带有L2正则化项的回归模型称为岭回归, 带有L1正则化项的回归称为Lasso回归.
1. 岭回归
引用百度百科定义.
岭回归(英文名：ridge regression, Tikhonov regularization)是一种专用于共线性数据分析的有偏估计回归方法，实质上是一种改良的最小二乘估计法，通过放弃最小二乘法的无偏性，以损失部分信息、降低精度为代价获得回归系数更为符合实际、更可靠的回归方法，对病态数据的拟合要强于最小二乘法。
通过定义可以看出, 岭回归是改良后的最小二乘法, 是有偏估计的回归方法, 即给损失函数加上一个正则化项, 也叫惩罚项(L2范数), 那么岭回归的损失函数表示为
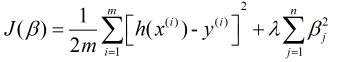
其中, m是样本量, n是特征数,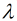 
是惩罚项参数(其取值大于0), 加惩罚项主要为了让模型参数的取值不能过大. 当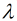趋于无穷大时, 对应
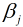趋向于0, 而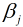表示的是因变量随着某一自变量改变一个单位而变化的数值(假设其他自变量均保持不变), 这时, 自变量之间的共线性对因变量的影响几乎不存在, 故其能有效解决自变量之间的多重共线性问题, 同时也能防止过拟合.
2. Lasso回归
岭回归的正则化项是对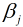求平方和, 既然能求平方也就能取绝对值, 而Lasso回归的L1范数正是对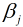取绝对值, 故其损失函数可以表示为
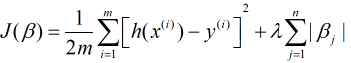
当只有两个自变量时, L1范数在二维上对应的图形是矩形(顶点均在坐标轴上, 即其中一个回归系数为0), 对于这样的矩形来说其顶点更容易与同心椭圆(等值线)相交, 而相交的点则为最小损失函数的最优解. 也就是说Lasso会出现回归系数为0的情况. 对于L2范数来说则是圆形,其不会相交于坐标轴上的点, 自然也就不会出现回归系数为0的情况. 当然多个自变量也是同样的道理
3. 岭回归和Lasso回归对比
相同点:
1. 岭回归和Lasso回归均是加了正则化项的线性回归模型, 本质上它们都是线性回归模型.
2. 两者均能在一定程度上解决多重共线性问题, 并且可以有效避免过拟合.
3. 回归系数均受正则化参数的影响, 均可以用图形表示回归系数和正则化参数的关系, 并可以通过该图形进行变量以及正则化参数的筛选.
不同点:
1. 岭回归的回归系数均不为0, Lasso回归部分回归系数为0
以上便是我本次分享的内容，如有任何疑问，请在下方留言，或在公众号【转行学数据分析】联系我！！！
