线性回归, 是回归分析中的一种, 其表示自变量与因变量之间存在线性关系. 回归分析是从数据出发, 考察变量之间的数量关系, 并通过一定的数学关系式将这种关系描述出来, 再通过关系式来估计某个变量的取值, 同时给出该估计的可靠程度. 下面我们从一元线性回归开始说起.
1. 一元线性回归
在回归分析中如果只涉及一个自变量(用来预测的变量)和一个因变量(要预测的变量), 这时就称为一元回归, 如果自变量与因变量之间存在线性关系, 那么此时的回归就称为一元线性回归.
1.1 模型
假设自变量x和因变量y存在线性关系, 那么x和y的线性关系函数可以表示为:
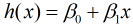
由于该函数是假设x和y存在线性关系, 因此该函数可以称为假设函数. 我们把描述因变量y和自变量x关系的函数称为回归模型, 故该函数又称一元线性回归模型.其中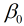
和
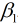称为模型参数, 不同的参数将会构造不同的模型, 因此构建模型的关键之处在于选择参数, 怎么样才能算好的参数呢?
由于我们构建模型的最终目的是用来预测, 因此好参数构建的模型应该具备很好的预测能力, 也就是说预测值和实际值差异很小, 我们把预测值h(x)与实际值y之间的差异称为误差. 对于某个值来说误差就是h(xi)-yi, 对于整个模型来说, 则是对所有误差进行求和, 但由于误差中有正负之分, 因此会产生误差相互抵消, 为了避免存在这种抵消问题, 对误差进行平方求和, 再对其求平均, 故有平均误差平方和
, 其表示为
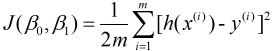
其中, m是样本量. h(x(i))表示第i个预测值, 与之对应的实际值则是y(i).
这种误差可以认为是实际值或者期望值的损失, 故该误差函数可以称为损失函数(有时也称为代价函数). 我们可以根据损失函数数值最小来选出最优模型(很好的预测能力).
1.2. 算法
这里我将介绍两种基于损失函数最小的算法: 梯度下降法和最小二乘法.
什么是梯度? 引出百度百科定义:
梯度的本意是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）。
在单个自变量函数曲线中, 梯度也就是曲线上某点处的斜率, 而对于我们的损失函数来说, 其有两个自变量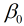和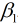, 故这两个自变量与损失函数将构成三维曲面.
可以将这三维曲面想象成一座山, 我们现在的目标是山底, 我们要想最快下山, 就需要走最陡峭的方向, 而最陡峭的方向可以看成是当前方向(下山方向)中变化最大的反方向. (其中, 变化最大的方向是指从下山改为上山, 与目标不符, 故取其反方向, 即最大的反方向).（具体来说就是：梯度的方向表示给定的某点上升最快的方向，而这个与我们下山的目标相反，故取其反方向，即梯度的反方向是下降最快的方向。）
梯度下降法与下山过程类似, 我们的目标是求出使得损失函数数值最小的最优解. 具体过程就是给定一个初始位置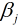
, 沿着梯度的反方向(也就是负的梯度)走一个步长的距离, 更新当前位置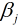, 如此反复, 直至找到使得损失函数最小的最优解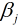, 可以表示为:
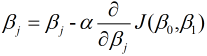
其中,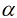 
为学习效率, 也称为步长, 等号右边的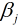为每次更新之前的模型参数(j=0,1), 即每走负梯度个步长, 更新一次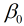和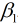, 而且这两者是同步更新. 具体的求解过程如下:
首先是微分的求解, 该部分需要链式法则, 公式为
由于在实际中, 往往很难直接求解z对x的微分, 但引入y这个"中介"就可以将问题转化为求z对y的微分和y对x的微分, 这就相当于分数约分的一个过程.
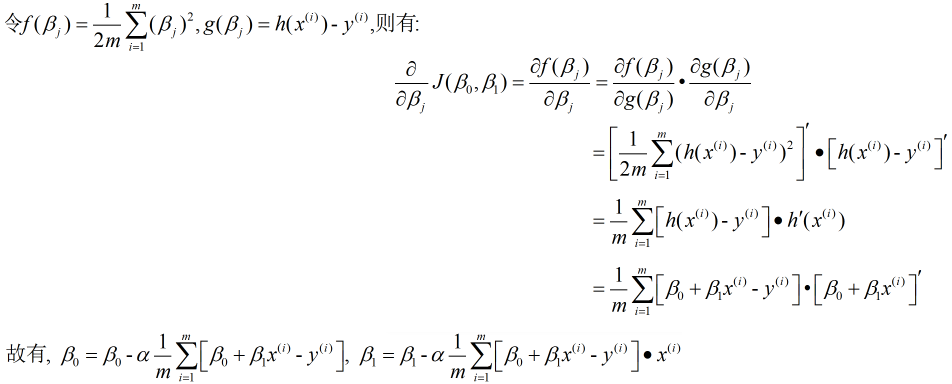
从计算过程中可以看出, 该算法在选择负的梯度方向时考虑到全部训练数据, 故该算法又称为批量(Batch)梯度下降法. 通过以上原理也可得知, 该算法是一个迭代求最优解的过程, 下面我们介绍一种可以直接一步到位的算法.
2. 最小二乘法
最小二乘法又称最小平方法, 即平均误差平方和最小, 也就是我们的损失函数数值最小. 引出百度百科费马引理定义:
函数f(x)在点ξ的某邻域U（ξ)内有定义，并且在ξ处可导，如果对于任意的x∈U（ξ)，都有f(x)≤f(ξ) (或f(x)≥f(ξ) )，那么f '(ξ）=0。
简单来说就是可导函数极值点处导数为0, 故分别对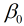和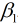求偏导, 并令其为0, 即:
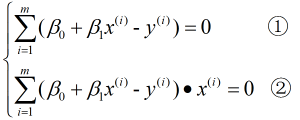
由①式可得: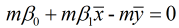 
, 故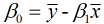
, 代入②式中, 可得:
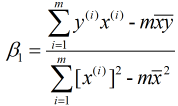
又由于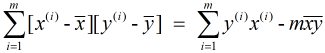
和 
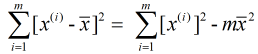, 故有:
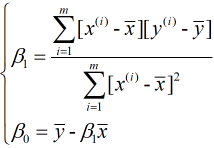
我们现在对一元线性回归介绍完了, 接下来看看多元线性回归.
2. 多元线性回归
多元线性回归与一元线性回归的区别在于自变量的个数, 一元是一个, 多元则是多个.
2.1 模型
假设多元线性回归中有多个自变量(x0, x1, x2,...xn), 那么多元线性回归模型的假设函数可以写成:
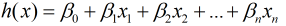
为了简化, 我们可以将假设函数写成矩阵的形式:
其中, x0=1
对应的其损失函数表示为(m表示样本量):
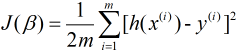
下面便是介绍求解最小损失函数的算法.
2.2 算法
同样介绍两种算法: 梯度下降法和最小二乘法.
1. 梯度下降法
与一元的方法类似, 不过这里需要注意的是对n个自变量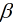
进行同步更新.即:
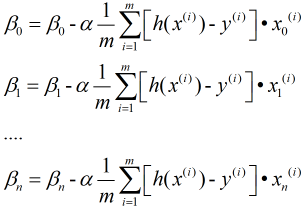
2. 最小二乘法
我们可以将损失函数转换为矩阵的形式:
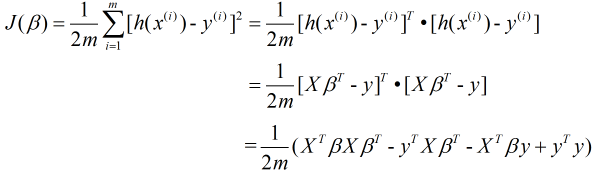
同样地, 令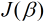
对
的偏导为0, 对于矩阵的运算需要用到以下公式:
然后套用公式:
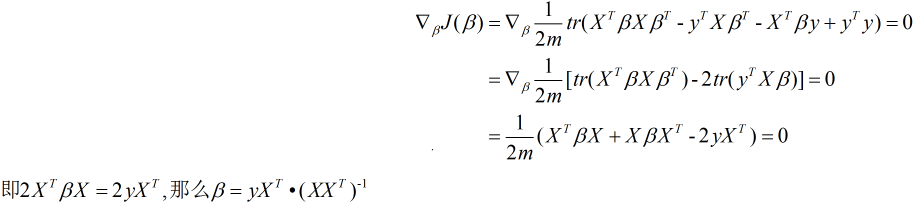
通过以上我们对一元和多元回归的模型以及算法均有所了解, 下面我们来看看这两大算法的优缺点.
3. 两大算法优缺点
3.1. 梯度下降法
优点
1. 在特征变量很多时, 能够很有效的运行
缺点
1. 容易依赖于步长和起始位置的选择, 因此需要多次尝试寻找合适的步长和起始位置.
2. 由于在每次更新当前位置需要计算全部训练数据, 因此其迭代速度过慢.
3.2 最小二乘法
优点
1. 直接应用公式计算即可, 学习效率高
缺点
1. 训练数据拟合的函数非线性的话, 则不能使用最小二乘法.
2. 需要计算
的逆矩阵, 如果逆矩阵不存在, 则没法应用最小二乘法.
3. 当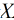
的样本特征n很大时, 计算的逆矩阵将会非常耗时, 或者说没法计算.
4. 算法优化问题
4.1 梯度下降法
上面我们介绍的梯度下降法是指批量梯度下降法, 即:
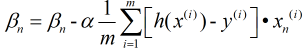
在批量梯度下降法中, 每次计算过程都考虑全部数据, 容易找到全局最优, 但数据量较大时将会非常耗费时间, 因此诞生了随机梯度下降法
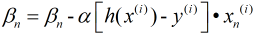
随机梯度下降法则是每次随机抽取一个样本进行计算, 可以大大提高学习效率, 但由于其具有随机性且仅有一个样本, 因此往往会导致不是最优解, 鉴于此, 产生了第三种方法: 小批量梯度下降法
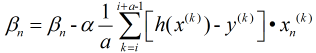
这是综合前两种方法产生的, 选取其中a个样本进行求解.
4.2 最小二乘法
若拟合函数非线性, 常常通过对数转换等方法将其转换为线性, 而且特征数量较少时直接运用公式进行计算即可.
4.3 小结
当训练数据特征数量较少时, 且拟合函数为线性, 则可以直接采用最小二乘法, 如果拟合函数非线性, 可以先对其进行对数转换再运用最小二乘法;
当训练数据特征数量较多时, 由于其对拟合函数无要求, 若数据量不大, 则可选用批量梯度下降, 若数据量很大, 则可以选用小批量梯度下降.
以上便是我本次分享的内容，如有任何疑问，请在下方留言，或在公众号【转行学数据分析】联系我！！！
