“物以类聚,人以群分”, 所谓聚类就是将相似的元素分到一"类"(有时也被称为"簇"或"集合"), 簇内元素相似程度高, 簇间元素相似程度低. 常用的聚类方法有划分聚类, 层次聚类, 密度聚类, 网格聚类, 模型聚类等. 我们这里重点介绍划分聚类.
1. 划分聚类
划分聚类, 就是给定一个样本量为N的数据集, 将其划分为K个簇(K<N), 每一个簇中至少包含一个样本点.
大部分的划分方法是基于距离的, 即簇内距离最小化, 簇间距离最大化. 常用的距离计算方法有: 曼哈顿距离和欧几里得距离. 坐标点(x1, y1)到坐标点(x2, y2)的曼哈顿距离和欧几里得距离分别表示为:
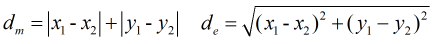
为了达到全局最优解, 传统的划分法可能需要穷举所有可能的划分点, 这计算量是相当大的. 而在实际应用中, 通常会通过计算到均值或中心点的距离进行划分来逼近局部最优, 把计算到均值和到中心点距离的算法分别称为K-MEANS算法和K-MEDOIDS算法, 在这里只介绍K-MEANS算法.
2. K-MEANS算法
K-MEANS算法有时也叫快速聚类算法, 其大致流程为:
第一步: 随机选取K个点, 作为初始的K个聚类中心, 有时也叫质心.
第二步: 计算每个样本点到K个聚类中心的距离, 并将其分给距离最短的簇, 如果k个簇中均至少有一个样本点, 那么我们就说将所有样本点分成了K个簇.
第三步: 计算K个簇中所有样本点的均值, 将这K个均值作为K个新的聚类中心.
第四步: 重复第二步和第三步, 直到聚类中心不再改变时停止算法, 输出聚类结果.
显然, 初始聚类中心的选择对迭代时间和聚类结果产生的影响较大, 选不好的话很有可能严重偏离最优聚类. 在实际应用中, 通常选取多个不同的K值以及初始聚类中心, 选取其中表现最好的作为最终的初始聚类中心. 怎么算表现最好呢? 能满足业务需求的, 且簇内距离最小的.
簇内距离可以簇内离差平方和表示:
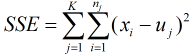
其中, K表示K个簇, nj表示第j个簇中的样本个数, xi表示样本, uj表示第j个簇的质心, K-means算法中质心可以表示为:
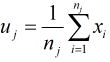
3. 优缺点及注意事项
优点:
1. 原理简单, 计算速度快
2. 聚类效果较理想.
缺点:
1. K值以及初始质心对结果影响较大, 且不好把握.
2. 在大数据集上收敛较慢.
3. 由于目标函数(簇内离差平方和最小)是非凸函数, 因此通过迭代只能保证局部最优.
4. 对于离群点较敏感, 这是由于其是基于均值计算的, 而均值易受离群点的影响.
5. 由于其是基于距离进行计算的, 因此通常只能发现"类圆形"的聚类.
注意事项:
1. 由于其是基于距离进行计算的, 因此通常需要对连续型数据进行标准化处理来缩小数据间的差异.(对于离散型, 则需要进行one-hot编码)
2. 如果采用欧几里得距离进行计算的话, 单位的平方和的平方根是没有意义的, 因此通常需要进行无量纲化处理
以上便是我本次分享的内容,如有任何疑问,请在下方留言,或在公众号【转行学数据分析】联系我!!!





