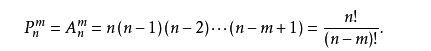
全排列
class Program
{
private static void Perm(int[] data, int k, ref int count)
{
int size = data.Length;
if (k == size - 1)
{
count++;
Console.WriteLine(string.Join(',', data));
}
else
{
for (int i = k; i < size; ++i)
{
if (i != k)
Swap(ref data[i], ref data[k]);
Perm(data, k + 1, ref count);
if (i != k)
Swap(ref data[i], ref data[k]);
}
}
}
private static void Swap(ref int a, ref int b)
{
b = Interlocked.Exchange(ref a, b);
}
static void Main(string[] args)
{
int n;
string nStr;
while (true)
{
while (true)
{
Console.WriteLine("输入一个正整数:");
nStr = Console.ReadLine();
if (int.TryParse(nStr, out n))
{
break;
}
}
var data = Enumerable.Range(1, n).ToArray();
int count = 0;
Perm(data, 0, ref count);
Console.WriteLine($"总计{count}种排列方式。");
}
}
}

组合
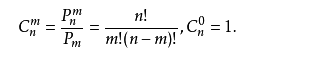
方法1: n个元素里取m个, 相当于先选中一个,然后从剩下的n-1个元素中取m-1个
class Program
{
public static void Combine(int[] data, int k, int m, int[] indexArr, ref int count)
{
int n = data.Length;
for (int i = (k == m ? n - 1 : indexArr[k] - 1); i >= 0; i--)
{
indexArr[k - 1] = i;
if (k > 1)
{
Combine(data, k - 1, m, indexArr, ref count);
}
else
{
count++;
Console.WriteLine(string.Join(",", indexArr.Select(c => data[c])));
}
}
}
static void Main(string[] args)
{
int n = 0, m = 0;
string nStr, mStr;
while (true)
{
while (true)
{
Console.WriteLine("输入n:");
nStr = Console.ReadLine();
Console.WriteLine("输入m:");
mStr = Console.ReadLine();
if (int.TryParse(nStr, out n) && int.TryParse(mStr, out m) && m > 0 && n >= m)
{
break;
}
}
var data = Enumerable.Range(1, n).ToArray();
int count = 0;
var indexArr = new int[m];
Combine(data, m, m, indexArr, ref count);
Console.WriteLine($"从{n}个元素中取{m}个元素,总计{count}种组合方式。");
}
}
}
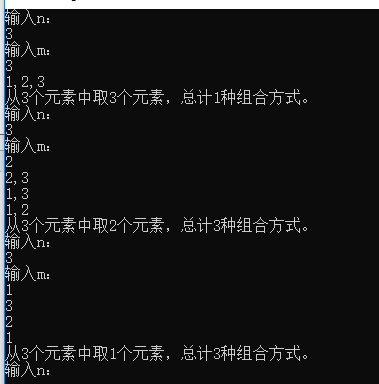
方法2:选择第一个,选择第二个,直到选够m个
class Program
{
public static void Combine2(int[] data, int k, int m, List<int> indexList, ref int count)
{
int selected = indexList.Count;
int n = data.Length;
if (selected == m)
{
count++;
Console.WriteLine(string.Join(",", indexList.Select(c => data[c])));
}
else
{
//选一个, 剩余的元素需要足够选出m个。
for (int i = k; i < n - m + selected + 1; i++)
{
indexList.Add(i);
Combine2(data, i + 1, m, indexList, ref count);
indexList.RemoveAt(indexList.Count - 1);
}
}
}
static void Main(string[] args)
{
int n = 0, m = 0;
string nStr, mStr;
while (true)
{
while (true)
{
Console.WriteLine("输入n:");
nStr = Console.ReadLine();
Console.WriteLine("输入m:");
mStr = Console.ReadLine();
if (int.TryParse(nStr, out n) && int.TryParse(mStr, out m) && m > 0 && n >= m)
{
break;
}
}
var data = new int[n];
for (int i = 0; i < n; i++)
{
data[i] = i + 1;
}
int count = 0;
var outList = new List<int>();
Combine2(data, 0, m, outList, ref count);
Console.WriteLine($"从{n}个元素中取{m}个元素,总计{count}种组合方式。");
}
}
}

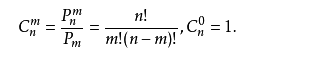



 浙公网安备 33010602011771号
浙公网安备 33010602011771号