如题。
显然,八皇后问题可以用栈来解决。
突然想试试用一维数组的下标和值,表示入栈的皇后在棋盘上的位置,就有了下面的c#代码:
using System; namespace ConsoleApp1 { class Program { //使用一维数组表示栈 // 用法:a[3]=5表示第三行第五列入栈 // main函数中的n指向靠近栈顶的空元素 static int[] a = new int[8]; static void Main(string[] args) { int i, n = 0, c = 0; //此处赋初值仅是为了使刚进循环时,i为0 a[0] = -1; do { //结合n--,i=a[n]表示出栈操作 i = a[n]; //结合后面的for循环,i++表示从出栈元素代表位置的后一个元素继续扫描 i++; for (; i < 8; i++) { if (isOK(n, i)) { a[n] = i;//入栈 if (n == 7) { c++; if (c == 1) { Console.WriteLine($"第{c}种解法:"); for (int j = 0; j < a.Length; j++) { Console.WriteLine($"({j},{a[j]})"); } } } else { n++; //为了使for循环的i从0重新开始 i = -1; } } } //当前行扫描完毕,回到上一行继续扫描 //把n看成栈顶的空单元格指针,这个操作也是“出栈”的前奏 n--; } while (n >= 0); Console.WriteLine($"共有{c}种解法。"); } static bool isOK(int x, int y) { bool myb = true; for (int i = 0; i < x; i++) { if (a[i] == y || i - a[i] == x - y || i + a[i] == x + y) { myb = false; break; } } return myb; } } } //原始思路: //n = 0 //第n行每个格子能否落子 //* 每个格子 //能 不能 //(第七行,结束) //(不是第7行) //压栈 //n++ 下一个 //*格子全部走完 //*n-- //*退栈
我是先写了后面的思路,再编的代码,然后稍微优化了一点点,添加了程序注释。
使用递归解八皇后问题,思考起来容易一些,写代码也更轻松。
思路:
fangGe(int n)表示在第n行和它后面的行放皇后。具体做法:
如果要放的是第八行(行标从0开始),说明前面(0-7行)已经摆出了8皇后的正确位置,这里输出结果就行了。
否则
1、第n行,从左到右,一个格子一个格子看。能放就放(放皇后就是格子里的值为1);不能放拉倒。
(如果能放)
2、放下之后,放它后面的所有行。即:执行fangGe(int n+1)。后面能不能放,输不输出结果,交给后面代码的去考虑。
3、”2“执行完以后,说明这个格子的使命完成,把它置为0,再看下一格。
java程序代码如下:
public class App { static int[][] a = new int[8][8]; static int c = 0, printNo = 5; public static void main(String[] args) throws Exception { fangGe(0); System.out.println("共有解法" + c + "种"); } public static void fangGe(int n) { if (n == 8) { c++; if (c == printNo) { System.out.println("第" + printNo + "种解法:"); showArray(); } return; } for (int i = 0; i < 8; i++) { if (nengFang(n, i)) { a[n][i] = 1; fangGe(n + 1); a[n][i] = 0; } } } public static boolean nengFang(int x, int y) { int hang = x, lie = y; boolean flag = true; while (--hang >= 0 && --lie >= 0) { if (a[hang][lie] == 1) { flag = false; } } if (!flag) { return flag; } hang = x; lie = y; while (--hang >= 0 && ++lie <=7) { if (a[hang][lie] == 1) { flag = false; } } if (!flag) { return flag; } hang = x; lie = y; while (--hang >= 0) { if (a[hang][lie] == 1) { flag = false; } } return flag; } static void showArray() { for (int i = 0; i < a.length; i++) { for (int j = 0; j < a[i].length; j++) { System.out.print(a[i][j] + "\t"); } System.out.println(); } } }
运行结果:
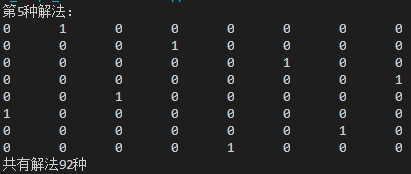
分类:
上课用内容







【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· go语言实现终端里的倒计时
· 如何编写易于单元测试的代码
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· ollama系列01:轻松3步本地部署deepseek,普通电脑可用
· 25岁的心里话
· 按钮权限的设计及实现