博文介绍
对于初学者来说，GNN还是好理解的，但是对于GCN来说，我刚开始根本不理解其中的卷积从何而来！！ 这篇博文分为两部分，第一部分是我对GNN的理解，第二部分是我个人对GCN中卷积的理解。
GNN
看了B站上up主小淡鸡的视频（视频：传送门）收益匪浅，我认为，GNN的目的就是怎样聚合各节点之间的信息。
GNN的流程
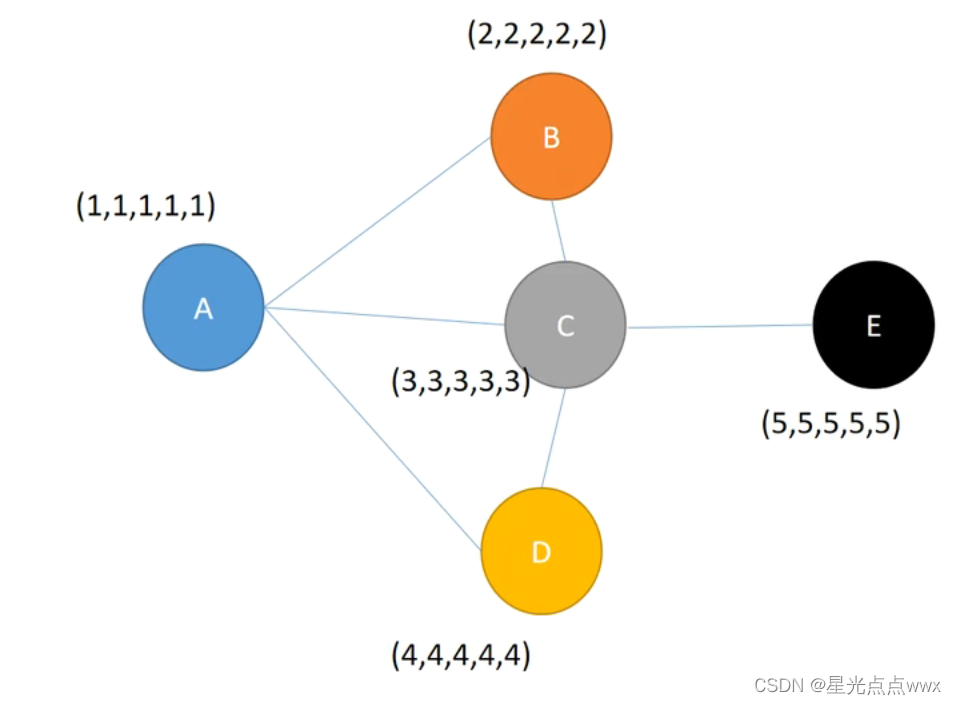
聚合
以上图\(A\)节点为例，\(A\)的邻居是节点\(B, C, D\), 经过一次聚合后：聚合到的信息为：
邻居信息\(N = a \times (2,2,2,2,2) + b \times (3,3,3,3,3) + c \times (4,4,4,4,4)\)
这里\(a,b,c\)都是权重参数
更新
\(A = \sigma (W((1,1,1,1,1))+ \alpha \times N)\)
\(\sigma\)是激活函数（relu，sigmoid 等）这里有点像普通神经网络的线性层。
\(W\)是模型需要学习的参数。
循环
图经过一次聚合后：
\(A\)有节点\(B, C, D\)的信息
\(B\)有节点\(A, C\)的信息
\(C\)有节点\(A, B, D, E\)的信息
\(D\)有节点\(A, C\)的信息
\(E\)有节点\(C\)的信息
第二次聚合，再以\(A\)节点为例，此时\(A\)聚合\(C\)的时候，\(C\)中有上一层聚合到的\(E\)的信息，所以这时\(A\)获得了二阶邻居\(E\)的特征。
GCN
GCN的卷积意义难以理解，我接下来会用图片(image)的卷积来讲解。
首先看一下公式：$$
H^{(l+1)} = \sigma (\tilde{D}^{-1/2} \tilde{A} \tilde{D}^{1/2} H^{(l)} W^{(l)}) $$
这里\(A\)是邻接矩阵， \(\tilde{D}\)是\(\tilde{A}\)的行求和所组成的对角阵, 也就是节点的度矩阵。
公式推导(物理意义)
先看这个图
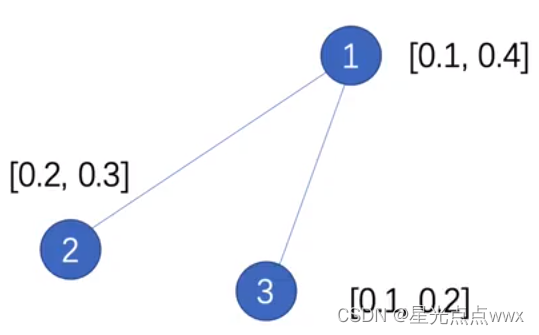
该图的邻接矩阵\(A\)：
节点特征值\(H^{(l)}\)为：
我们首先看一下\(A H^{(l)}\)是啥：
可以看到这做到了汇聚（上一节提到的GNN）的作用
再加上自己的特征值，也就是\(\tilde{A} H^{(l)}\) （这里\(\tilde{A} = A + I\)）：
这些矩阵乘法从数学上实现了个节点之间的聚合
Note：公式：\(H^{(l+1)} = \sigma (\tilde{D}^{-1/2} \tilde{A} \tilde{D}^{1/2} H^{(l)} W^{(l)})\)中的\(\tilde{D}^{-1/2}\)的作用其实是为了归一化
理解GCN，卷积从何而来
首先， 以两层的特征提取器举例：
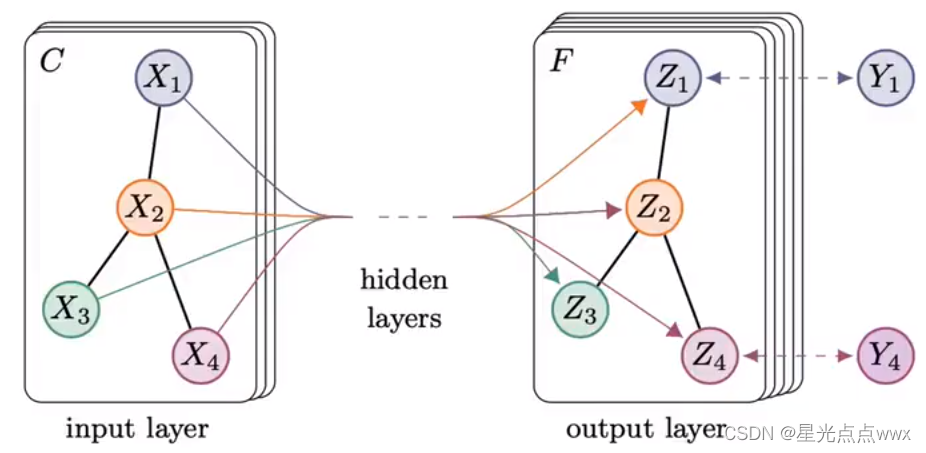
这里\(\hat{A} = \tilde{D}^{-1/2} \tilde{A} \tilde{D}^{1/2}\)， \(X\)是特征向量， \(W\)是要学习的参数。
类比图片
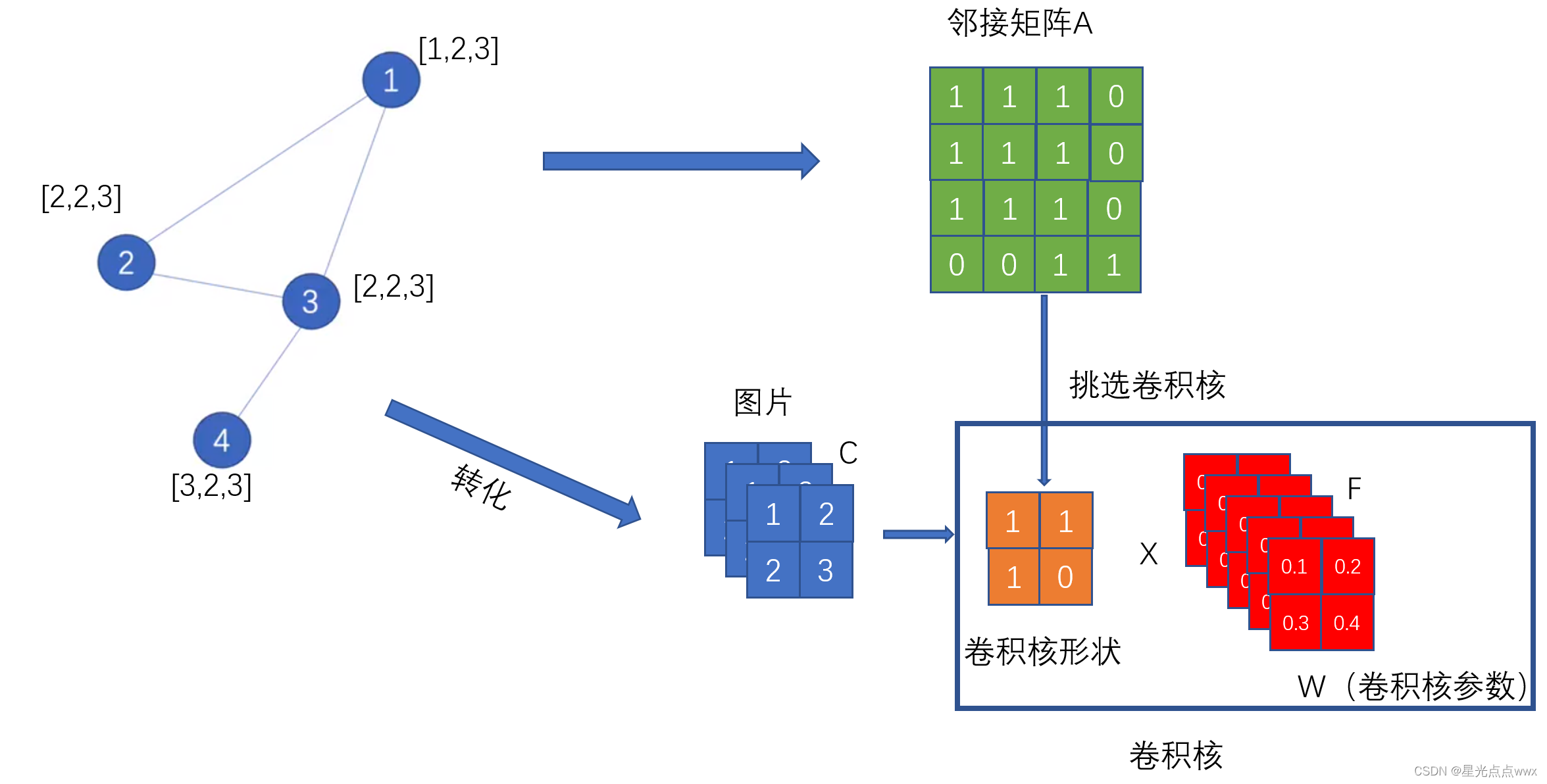
我们可以这么理解，如下图，图(graph) 的分类可以近似成 图片(image) 的像素级分类（即对每个像素(节点)进行分类）
- 每个节点代表一个像素，其特征维度(向量\(X_1\)的长度)代表通道数\(C\)
- 归一化后的邻接矩阵 \(\hat{A}\) 的每一行可以认为卷积核的形状参数 (比如说，对1号像素(节点)使用3X3的卷积核，对2号像素(节点)使用2X2的卷积核，等等)，注意这里\(\hat{A}\)是固定不变的。
- W就是所对应的卷积核参数
好， 现在根据形状参数 \(\hat{A}\) 给 图片\(I \in \mathbb{R}^{N \times C}\) 做卷积(这里图片有N个像素)，得到特征图\(H^{(2)} \in \mathbb{R}^{N \times F}\)，现在特征图的每个像素的特征值维度是\(\mathbb{R}^{1 \times F}\)，因为是像素级分类，我们就可以让每个像素进入分类器（全连接层）了！这样像素级(GCN)分类就做完了.
