这篇博客是啥?
icarl 这篇论文以算法伪代码的形式来展示作者的想法,对于我来说有点难理解,所以做个笔记。
这篇博客只对方法进行分析(论文的第二节就讲方法, 我很少见这种论文格式,一般第二节是Related work)
论文地址
iCaRL: Incremental Classifier and Representation Learning(CVPR 2017)
前提:什么是增量学习(终身学习 LongLife Learning)?
直接上图, 这是人类的增量学习过程

增量学习是使模型具有跟人一样的学习能力,即学了新知识不会忘了旧知识
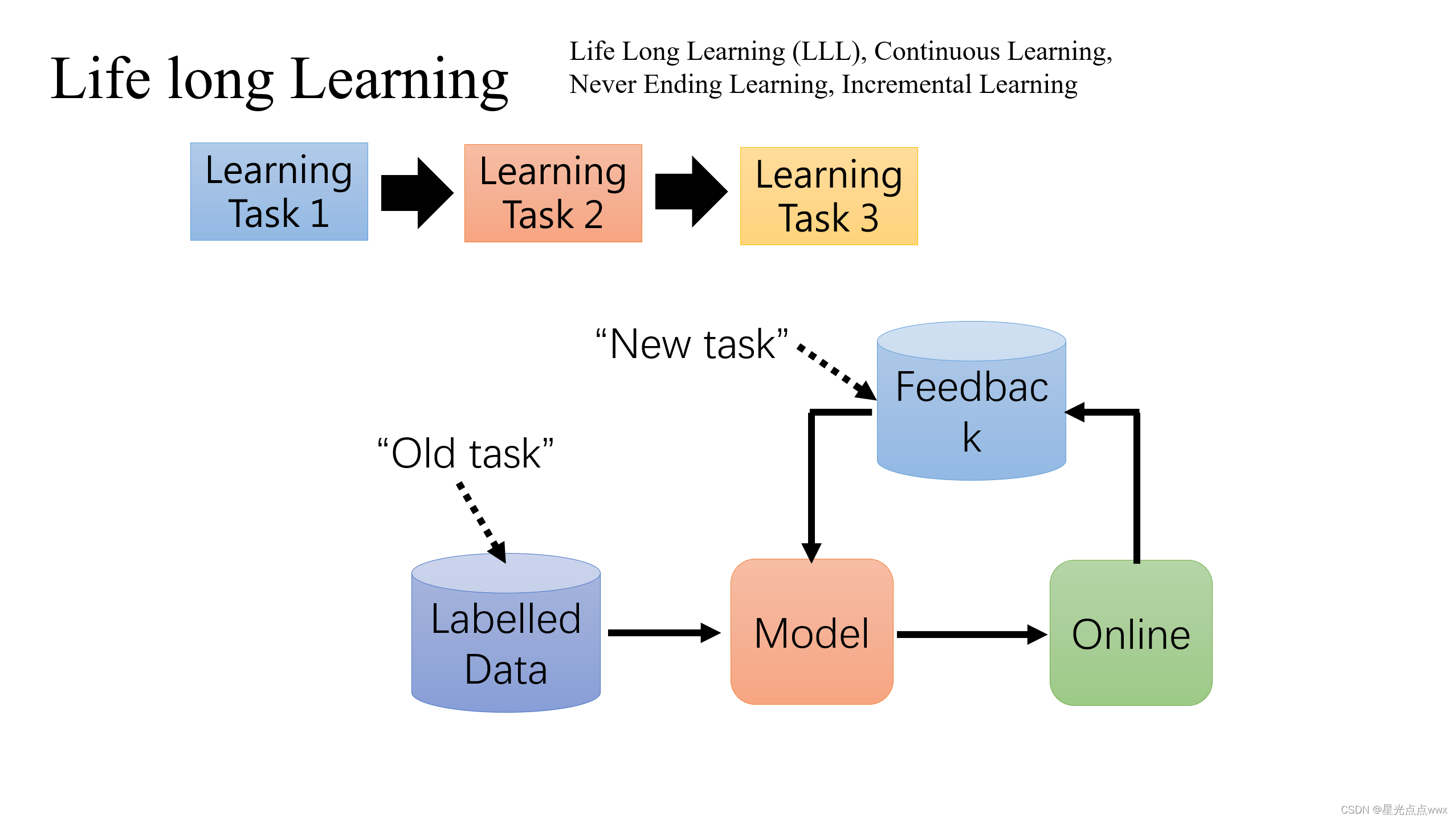
如上图, 就比如淘宝的恶心的推荐系统, 一开始新用户注册,新用户的爱好淘宝是不知道的,所以,淘宝会给新用户推荐大众化的商品,这里推荐系统模型的输出(应该叫prediction)是从“old task” 数据集来的(由“old task” 数据集训练来的)。然后,新用户开始选购商品, 过一段时间,淘宝的服务器就接收到反馈了(用户选了啥类型的商品),模型就根据新用户的反馈(用户选的商品的新的类别)继续训练,这样模型输出就是 “大众化商品” + “刚才选的”
方法
作者最先给出的算法伪代码1是关于分类的, 如下图
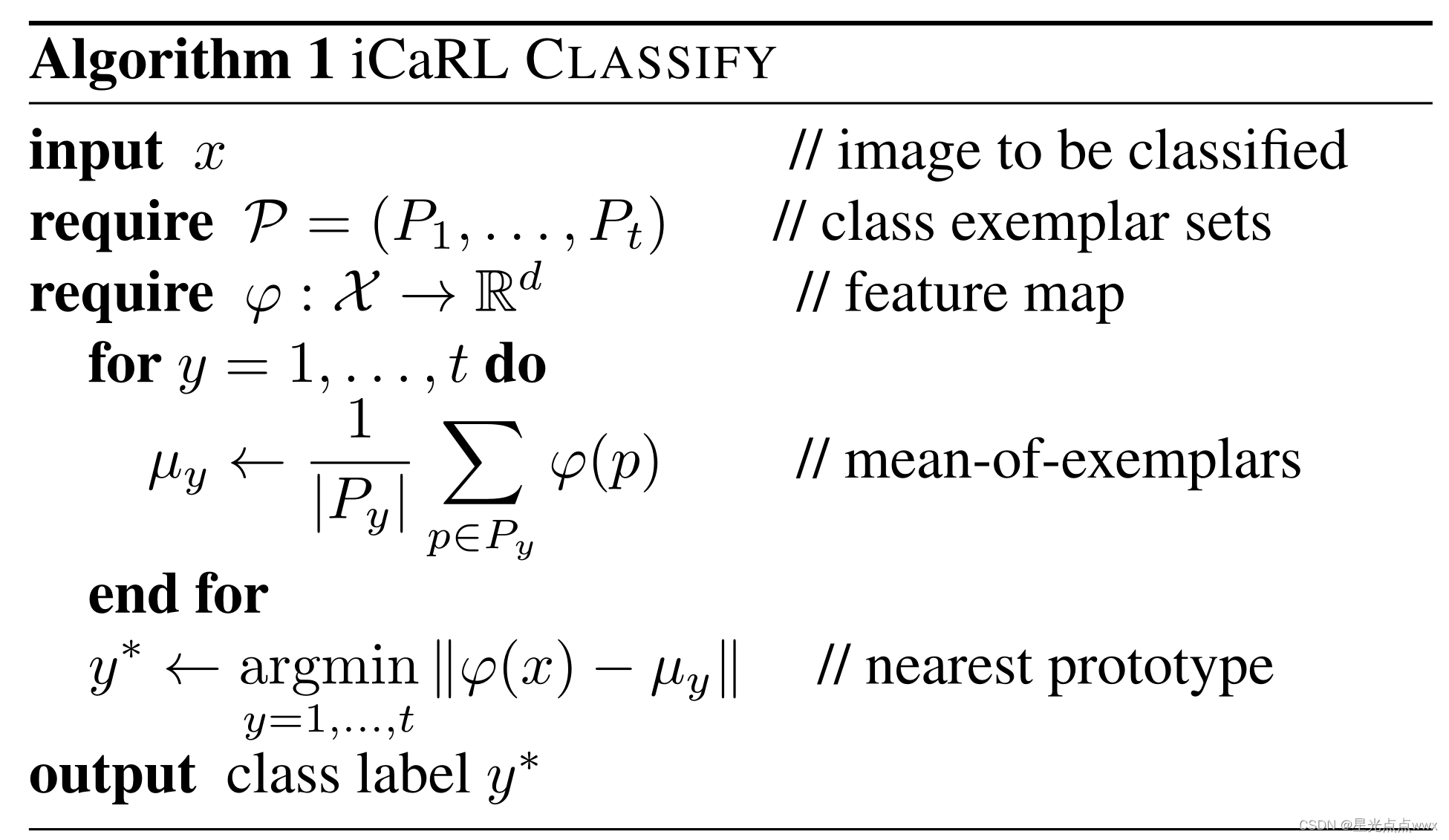
作者在这里引入了最近平均样本分类规则(nearest-mean-of-exemplars rule), 先不着急看伪代码咱们先看看作者是怎样解释传统方法的
传统方法
- 咱们理解的分类模型:首先, \(\varphi\)是特征提取器,一般传统的方法是在特征提取器\(\varphi\)后面直接接入分类器, 并且传统的分类器一般是全连接层(这里用FC表示),整体网络结构可以表示为FC(\(\varphi\)(x)), 这里x为输入图片。
- 论文的解释: 论文给的分类公式(好像有点难理解):
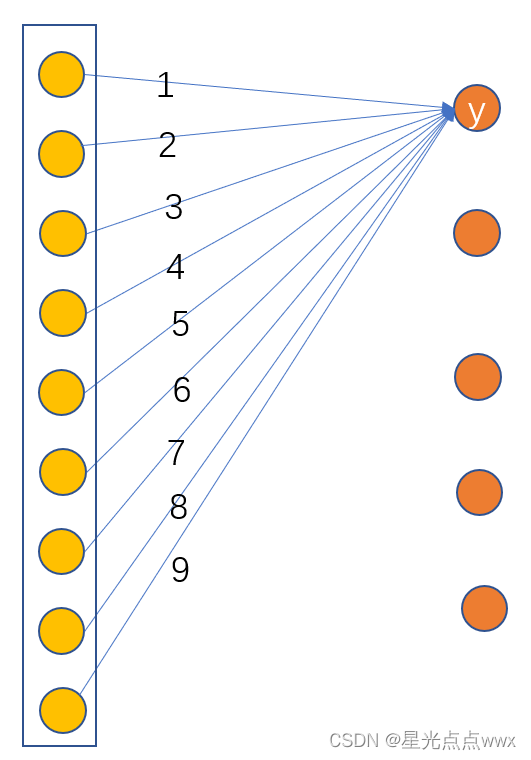
这里\(y\)表示第“\(y\)”类,\(w_y^T\)表示第“\(y\)”类权重(如下图),我的理解:论文这里其实是把FC拆开了,FC的数学表达式是\(Wx+b\), 这里\(W\)是一个矩阵被拆成\(\{w_1, . . . , w_t \}∈ \mathbb{R}^d\) 共t个向量,如下图, 对于第“\(y\)”类(这里在输出端是的一个节点)那么\(w_y = [1,2,3,4,5,6,7,8,9]\)
最近平均样本分类规则(nearest-mean-of-exemplars rule)
作者觉得传统方法(模型FC(\(\varphi\)(x))), 分类器FC和特征提取器\(\varphi\)的参数必须同步的更新,即每当\(\varphi\)改变时,所有\(w_1 , . . . , w_t\)都必须更新。否则,网络输出就会发生不可控的变化,这可以看作是灾难性的遗忘。 现在,我们再看看算法1
作者为每一个类(模型见过的)保存了一定的样本,例如模型见过t个类,就会保存t个样本集\(P_1,...,P_t\)(样本怎样挑选见下一节,这里假设挑选好了),然后对每一类的特征图求均值,例如,对于第y类有如下公式
其实这里作者想表达的是特征提取器\(\varphi\)对每一类的响应的均值,啥意思呢?就比如说我现在已经把所有样本集的均值都求了一遍得到\(\{\mu _{1}, ...\mu _{t}\}\), 现在输入了一张未标签的图片x,它的特征图是\(\varphi(x)\),我想预测它属于哪一类\(y^*\),现在就可以拿\(\varphi(x)\) 和 \(\{\mu _{1}, ...\mu _{t}\}\) 一一对比, 如下公式, 找一个y使得\(\parallel \varphi(x) - \mu _{y} \parallel\)最小。
再回到与传统方法对比,最近平均样本分类“没有分类器”,即分类器没有参数。请注意,由于我们使用的是归一化特征向量(向量模长为1),等式(2)可以等效地写成 \(y^* = \arg \max _{y} \mu _{y} \varphi(x)\)。现在最大的问题解决了,下面讨论样本挑选。
样本挑选
上一节,说拿\(\varphi(x)\) 和 \(\{\mu _{1}, ...\mu _{t}\}\) 一一对比得出最相近的\(\mu\),\(\mu\)的下标就是预测的类别,所以说\(\mu\)的值至关重要,然而上一节的\(\mu\)是从样本集P得出来的(假设记作\(\mu ^{p}\)),这个和整个数据集\(X\) 得出来的\(\mu\)(假设记作\(\mu ^{X}\)),并不一定是相等的(为啥要相等?新图片x肯定得跟整个数据集\(X\)的均值做对比啊,样本集P只是在这里近似替代\(X\)),问题就在于怎样使得\(\mu ^{X}\) 和 \(\mu ^{p}\) 尽可能相似,作者给出了算法4,如下图:

先求整个数据集\(X\) 的\(\mu ^X= \frac{1}{n} \sum _{x∈X} \varphi(x)\), 然后找出K个x, 使得其均值\(\frac{1}{k} [\varphi(x_k) + \sum _{j=1} ^{k-1}\varphi(x_j)]\)与\(\mu ^{X}\)最相近。 这里前K个x的均值为啥要拆开呢(k 和 1到k-1)?其实作者这里想给一个优先级 前k-1的更能拟合\(\mu ^X\)(把for循环走一遍就知道了,一开始k-1=0)。
然后在规定内存一定情况下,增加新类,可能会导致内存溢出,所以必须减少每一类的样本量,来为新类样本提供空间, 那怎么删除每一类的样本量呢,因为算法4挑选时有优先级,直接把末尾的样本删除即可, 如作者给出的算法5:

万事俱备只欠东风了!
增量学习 更新参数
之前我们保存了 每一类的均值\(\{\mu _{1}, ...\mu _{s-1}\}\),分类模型是 \(y^* = \arg \max _{y} \mu _{y} \varphi(x)\), 假设对于前s-1 类模型已经训练好了, 当后s ~ t 类开始增量学习该咋办, 这里作者用了表征学习,说白了还是记响应,对与新来的s类图片\(x ^s _i\),进老网络先过一遍,保存老模型对\(x ^s _i\)的响应\(\{ q _i ^1,...q _i ^{s-1}\}\), 这个可用作蒸馏损失(老模型是老师,新模型是学生)这样就可以保留以前的知识。下面就是损失函数
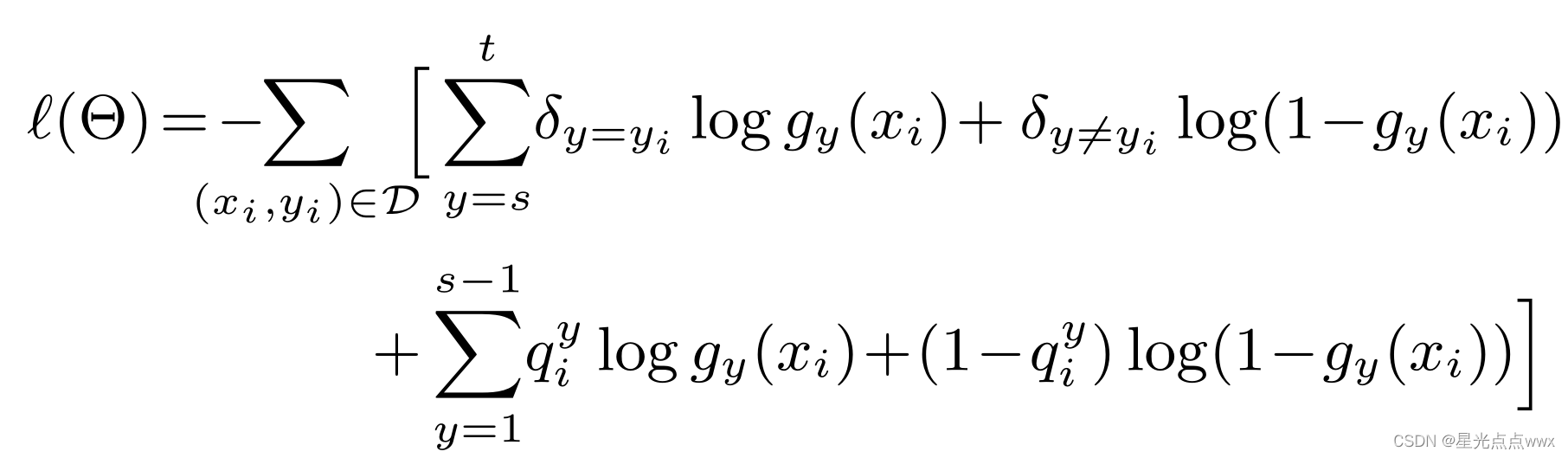
这里前一个求和是分类损失,有点像交叉熵损失, \(\delta _{y}\)离散情况下是独热码(像这样[0,0,1,0,0])
后面一个求和是蒸馏损失,是一个软标签(响应\(\{ q _i ^1,...q _i ^{s-1}\}\))的交叉熵。
好解释完了,上算法图:

增量学习 训练
将上面步骤联立起来, 大功告成!

个人感想
这篇论文是增量学习的基础中的基础, 结合数据驱动,结构驱动,蒸馏等方法。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号