算法执行时间需通过依据该算法编制的程序在计算机上运行时所消耗的时间来度量。而度量一个程序的执行时间通常有两种方法。(1)事后统计的方法。(2)事前分析估算的方法。因事后统计方法更多的依赖于计算机的硬件、软件等环境因素,有时容易掩盖算法本身的优劣。因此人们常常采用事前分析估算的方法。
两个N * N矩阵相乘。如 2 * 2的矩阵,
void CMatrixNN::ComputeN2(void) { const int n = 2; int a[n][n] = { {1, 2}, {1, 2} }; int b[n][n] = { {1, 2}, {1, 2} }; int result2[][n] = {0, 0, 0, 0}; for (int i = 0; i < n; i ++) for (int j = 0; j < n; j ++) { result2[i][j] = 0; for (int k = 0; k < n; k ++) result2[i][j] += a[i][k] * b[k][j]; } for (int l = 0; l < n; l ++) { for (int m = 0; m < n; m ++) cout << result2[l][m] << " "; cout << endl; } }
//输出
3 6
3 6
即使这个矩阵是2 * 2矩阵仍然需要三重循环来完成这个计算。一般情况下,算法中基本操作重复执行的次数是问题规模n的某个函数f(n),算法的时间量度记作T(n) = O(f(n))。表示随问题规模n的增大,算法执行时间的增长率和f(n)的增长率相同,称做算法的渐近时间复杂度(asymptotic time complexity),简称时间复杂度。
显然,被称做问题的基本操作的原操作应是其重复执行次数和算法的执行时间成正比的原操作,多数情况下它是最深层循环内的语句的原操作,它的执行次数和包含它的语句的频度相同。语句的频度(frequency count)指的是该语句重复执行的次数,例如,在下列3个程序段中:
(a){ ++x; z = 0; }
(b)for (int i = 1; i <= n; ++i) { ++x; z += x; }
(c)for (int j = 1; j <= n; ++j)
for (int k = 1; k <= n; ++k) { ++x; z += x; }
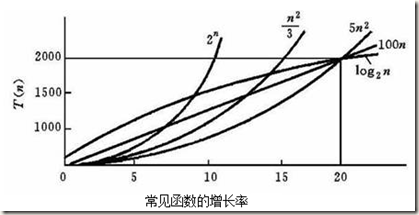
含基本操作“x增1”的语句的频度分别为1、n和n^2,则这3个程序段的时间复杂度分别为O(1)、O(n)和O(n^2),分别称为常量阶、线性阶和平方阶。算法还可能呈现的时间复杂度有对数阶O(log n)、指数阶O(2^n)等。不同数量级时间复杂度的性状如图所示。
从图中可见,我们应该尽可能选用多项式阶O(n^k)的算法,而不希望用指数阶的算法。
一般情况下,对一个问题(或一类算法)只需选择一种基本操作来讨论算法的时间复杂度即可,有时也需要同时考虑几种基本操作,甚至可以对不同的操作赋予不同的权值,以反映执行不同操作所需的相对时间,这种做法便于综合比较解决同一问题的两种完全不同的算法。
由于算法的时间复杂度考虑的只是对于问题规模n的增长率,则在难以精确计算基本操作执行次数(或语句频度)的情况下,只需求出它关于n的增长率或阶即可。例如,在下列程序段中:
for (int i = 2; i <= n; ++i)
for (j = 2; j <= i – 1;) { ++x; a[i][j] = x; }
语句 ++x 的执行次数关于n的增长率为n^2,它是语句频度表达式(n-1)(n-2)/2中增长最快的项。
有的情况下,算法中基本操作重复执行的次数还随问题的输入数据集不同而不同。例如在下列起泡排序的算法中:
void bubble_sort(int a[], int n)
{
for (int i = n - 1, change = TRUE; i >= 1 && change; --i)
change = FALSE;
for (int j = 0; j < i; ++j)
if (a[j] > a[j + 1]) { int temp = a[j]; a[j] = a[j + 1]; a[j + 1] = temp; change = TRUE; }
}//bubble_sort
“交换序列中相邻两个整数”为基本操作。当a中初始序列为自小至大有序,基本操作的执行次数为0;当初始序列为自大至小有序时,基本操作的执行次数为n(n-1)/2。对这类算法的分析,一种解决的办法是计算它的平均值,即考虑它对所有可能的输入数据集的期望值,此时相应的时间复杂度为算法的平均时间复杂度。如假设a中初始输入数据可能出现n!种的排列情况的概率相等,则起泡排序的平均时间复杂度Tavg(n)=O(n^2),然而,在很多情况下,各种输入数据集出现的概率难以确定,算法的平均时间复杂度也就难以确定。因此,另一种更可行也更常用的办法是讨论算法在最坏情况下的时间复杂度,即分析最坏情况以估算算法执行时间的一个上界。例如,上述起泡排序的最坏情况为a中初始序列为自大至小有序,则起泡排序算法在最坏情况下的时间复杂度为T(n)=O(n^2)。
实践中我们可以把事前估算和事后统计两种办法结合起来使用。以两个矩阵相乘为例,若上机运行两个10 * 10矩阵相乘,执行时间为12ms,则由算法的时间度T(n)=O(n^3)可估算两个31 * 31的矩阵相乘所需时间大致为(31/10)^3 * 12ms = 358ms(约等于)。