单纯形法
提出单纯形的思路
我们知道,线性规划(LP)问题如果有最优解,必可在某个极点(基本可行解)上达到。一个直观的想法是:对于LP问题,找出所有的基本可行解,然后逐个比较,即枚举法。但是事实上,时间开销会非常大,假设原问题中有n个变量,m个约束条件,则时间开销为$C^{m}_{n}$,而$C^{m}_{n}$会随着m,n的增大而迅速地增大。显然,这不可行。
换种思路:若从某一基本可行解出发,每次总是寻求比上一个更“好”的基本可行解,直至找到最优解。这样就可以大大减少计算量,其实这样的思想应用在非常多的地方,比如梯度下降等等。
如果我们要使用这种迭代的求解方法,我们需要解决下面的三个问题:
- (1) 如何判断当前的基本可行解是最优解(迭代终点);
- (2) 如何寻找下一个改善的基本可行解(迭代关系式);
- (3) 如何得到一个初始的基本可行解(迭代起点);
美国数学家丹奇格(G.B.Dantzig)解决了上面的三个问题,也就得到了一种快速求解LP问题的方法,我们称为单纯形法。
通过一个例子进行分析
举个例子。
问题描述
设有某LP问题如下
$max\ z=cx\\ s.t.
\left\{ \begin{gathered}
Ax=b \hfill \\
x\geq 0 \hfill \\
\end{gathered} \right.$
其中,$c=\begin{bmatrix}5&2&0&0&0\end{bmatrix}$,$x=\begin{bmatrix}x_1\\x_2\\x_3\\x_4\\x_5\end{bmatrix}$,$A=\begin{bmatrix}30&20&1&&\\5&1&&1&\\1&&&&1\\ \end{bmatrix}$,$B=\begin{bmatrix}160\\15\\4\end{bmatrix}$。
解:
令$B^{(0)}=(p_3,p_4,p_5)=\begin{bmatrix}1&&\\&1&\\&&1\end{bmatrix}$为基矩阵,即$x_3,x_4,x_5$为基变量,$x_1,x_2$为非基变量。
使用非基变量表示基变量,有$\left\{ \begin{gathered}
x_3=160-30x_1-20x_2 \hfill \\
x_4=15-5x_1-x_2 \hfill \\
x_5=4-x_1 \hfill \\
\end{gathered} \right.$。因此,目标函数的非基表示为$z=0+5x_1+2x_2$。
令$x_1=0,x_2=0$,则得到一个基本可行解为$x^{(0)}=(0,0,160,15,4)^T$,目标函数$z^{(0)}=0$,显然这不是最优解。我们需要换一组基变量(即从一个顶点移动到另一个顶点)。于是,我们选取$(x_1,x_2)$中的一个变量(换入基变量),$(x_3,x_4,x_5)$中的一个变量(换出基变量),进行换入换出。现在,假设换入基变量为$x_1$,下面确定换出基变量。(在这里我们称进行基变换的两个变量为换入基变量和换出基变量,也可以称为进基变量和离基变量)
由于$x_2$仍为非基变量,故$x_2$仍取零值。因此,有$\left\{ \begin{gathered}
x_3=160-30x_1 \hfill \\
x_4=15-5x_1 \hfill \\
x_5=4-x_1 \hfill \\
\end{gathered} \right.$由于有$x\geq 0$,因此$x_1=min\{160/30,15/5,4/1\}=3$,故$x_4$为换出基变量,这样得到一个新的基本可行解$x^{(1)}=(3,0,70,0,1)$,相应的基矩阵$B^{(1)}=(p_3,p_1,p_5)$,基变量为$x_3,x_1,x_5$,非基变量为$x_2,x_4$,对应的目标函数值$z^{(1)}=15>z^{(0)}=0$。因此,$x^{(1)}$是比$x^{(0)}$改善的基本可行解。
下面分析$x^{(1)}$是否是最优解。在上面我们得到目标函数值$z=0+5x_1+2x_2$,根据约束方程组,我们可以得到$x_1=3-\frac{1}{5}x_2-\frac{1}{5}x_4$,代入目标函数式,我们得到$z=15+x_2-x_4$。观察左式,我们发现非基变量$x_2$前的系数为正,增加$x_2$,目标函数值仍可以增大,或者说,让$x_2$做换入基变量,进行换入,我们有可能使目标函数值增大。因此,$x^{(1)}$不是最优解。
使用相同的方法,以$x_2$为换入基变量,我们得到$x_3$为换出基变量,得到新的基本可行解$x^{(2)}=(2,5,0,0,2)^T$,目标函数$z=20-\frac{1}{14}x_3-\frac{4}{7}x_4$,在左式中,我们可以看出非基变量$x_3$或$x_4$由零值增加,只会使得目标函数值$z$减少,故$x^{(3)}$是最优解。
下面归纳一下单纯形法的基本解题步骤。
单纯形法的基本过程
第一步:构造一个初始的基本可行解。
第二步:判断当前基本可行解是否为最优解。
第三步:若当前解不是最优解,则要进行基变换迭代到下一个基本可行解。
最优性检验
这一部分,我们来判断当前解是否是最优解。我们将目标函数化为如左的形式$z=z_0+\sum_{j=m+1}^{n}{\sigma_j\cdot x_j}$。我们称$\sigma_j$为非基变量$x_j$的检验数。有以下定理
若关于非基变量的所有检验数$\sigma_j\leq 0$成立,则当前基本可行解$x^*$就是最优解。
基变换
我们通过基变换迭代到下一个改善了的基本可行解。问题在于,我们如何选择换入基变量和换出基变量。
- (1) 换入基变量的选择 对于$z=z_0+\sum_{j=m+1}^{n}{\sigma_j\cdot x_j}$,若有两个以上的$\sigma>0$,则选最大$\sigma$。
- (2) 换出基变量的选择 假设换入基变量为$x_k$。在上一轮迭代中的多个基变量中,增长$x_k$最先达到0的基变量为换出基变量。
无穷多个最优解及无界解的判定
实际上,有些LP问题无解或者会有无穷多个解。这两类情况有些特殊,需要在迭代中进行额外的判断,防止程序陷入死循环或者出错。
- (1) 无穷多个最优解的判定 如果当前基本可行解$x^{(k)}$的所有非基变量的检验数$\sigma_i$满足$\sigma_i\leq 0$,且其中一个$\sigma_j=0$,则该LP问题有无穷多个最优解。
- (2) 无界解的判定 如果当前基本可行解$x^{(k)}$,其中一个非基变量$x_i$的检验数$\sigma_i>0$,且$x_i$对应的系数列向量$p_i=(a_1,a_2,...,a_m)$中,所有分量$a_j\leq 0$,则该线性规划问题具有无界解(或者称无最优解)。这个可能比较费解,换种说法,可能会容易理解一点:某次迭代中,对于换入基变量$x_i$,无法找到一个换出基变量,则此问题无界。
单纯形法的python实现
在编程的过程中,我们会思考一些具体的细节,也许会有新发现哦。
#python 3
import numpy as np
from itertools import combinations
# 实体类 Solution
# 控制类 Simplex
class Solution:
def __init__(self):
pass
def set_para(self,A,b,z):
# A m*n
# b m*1
# z 1*(m+1)
self.A=A
self.b=b
self.z=z
self.m,self.n=A.shape
self.x_index=[i for i in range(self.n)]
def get_init_solution(self):
for JB in combinations(range(self.n),self.m):
if self._is_solution(JB):
JB,JN=self._rearrange(JB)
self._set_JB_JN(JB,JN)
return True
return False
def _is_solution(self,JB):
B=np.hstack([self.A[:,i] for i in JB])
# B的行列式的值不为0,则B是一个可逆矩阵
if np.linalg.det(B):
return True
return False
def _rearrange(self,JB):
JN=[i for i in range(self.n) if i not in JB]
B=np.hstack([self.A[:,i] for i in JB])
N=np.hstack([self.A[:,i] for i in JN])
self.z=[self.z[0,i] for i in JB]+[self.z[0,i] for i in JN]+[self.z[0,-1]]
self.z=np.matrix([self.z],dtype=float)
# 将B转化为单位矩阵
# 即(B|N)x=b -> (I|B'N)x=B'b
self.A=np.hstack((np.eye(self.m),B.I*N))
self.b=np.dot(B.I,self.b)
# 相应的重新定义JN,JB
self.x_index=list(JB)+list(JN)
JB=[i for i in range(self.m)]
JN=[i for i in range(self.m,self.n)]
# 在目标函数中,使用非基变量替代基变量
for i in range(self.m):
_change=np.zeros((1,self.n+1))
_change[0,:self.n]=self.A[i,:]
_change[0,-1]=-self.b[i,0]
self.z-=_change*self.z[0,i]
return JB,JN
def _set_JB_JN(self,JB,JN):
self.JB=JB
self.JN=JN
def is_best(self):
best,inf_solution=True,False
for i in self.JN:
sigma=self.z[0,i]
if sigma>0:
best=False
elif sigma==0:
inf_solution=True
return best,inf_solution
def get_inVar(self):
greatest_sigma=0
for i in self.JN:
sigma=self.z[0,i]
if greatest_sigma<sigma:
greatest_sigma=sigma
inVar=i
return inVar
def get_outVar(self,inVar):
min_ratio=self.b[self.JB[0],0]/self.A[self.JB[0],inVar]
outVar=self.JB[0]
flag=False
for i in self.JB[1:]:
k=self.A[i,inVar]
if k>0:
flag=True
_tmp=self.b[i,0]/k
if _tmp<min_ratio:
min_ratio=_tmp
outVar=i
if flag==False:
return None
return outVar
def in_and_out(self,inVar,outVar):
self.A[:,[inVar,outVar]]=self.A[:,[outVar,inVar]]
self.x_index[outVar],self.x_index[inVar]=self.x_index[inVar],self.x_index[outVar]
self.z[0,inVar],self.z[0,outVar]=self.z[0,outVar],self.z[0,inVar]
B=np.hstack([self.A[:,i] for i in self.JB])
N=np.hstack([self.A[:,i] for i in self.JN])
# 将B转化为单位矩阵
# 即(B|N)x=b -> (I|B'N)x=B'b
self.A=np.hstack((np.eye(self.m),B.I*N))
self.b=np.dot(B.I,self.b)
# 在目标函数中,使用非基变量替代基变量
for i in range(self.m):
_change=np.zeros((1,self.n+1))
_change[0,:self.n]=self.A[i,:]
_change[0,-1]=-self.b[i,0]
self.z-=_change*self.z[0,i]
def getX(self):
x=[0]*self.n
for i in self.JB:
x[self.x_index[i]]=self.b[i,0]
return x
class Simplex:
def __init__(self):
self.solution=Solution()
# 0 正常,尚未得到最优解,继续迭代
# 1 无解,无界解
# 2 达到最优解
# 3 问题有无数个最优解
self.status=0
def set_para(self,A,b,z):
# A,b,z 需以矩阵的形式输入
self.solution.set_para(A,b,z)
def output_result(self):
self._main()
if self.status==1:
print("此问题无界")
elif self.status==2:
print("此问题有一个最优解")
elif self.status==3:
print("此问题有无穷多个最优解")
def _main(self):
# 获得初始可行解
self._get_init_solution()
if self.status==1:
return
while True:
print ("--------------------")
print ("z:",self.solution.z[0,-1])
print ("x:",self.solution.getX())
# 最优性检验
self._is_best()
if self.status in (2,3):
return
# 换入换出
self._mainloop()
if self.status in (1,2):
return
def _get_init_solution(self):
if self.solution.get_init_solution():
self.status=0
else:
self.status=1
def _is_best(self):
best,inf_solution=self.solution.is_best()
if best==True and inf_solution==False:
self.status=2
elif best==True and inf_solution==True:
self.status=3
else:
self.status=0
def _mainloop(self):
inVar =self.solution.get_inVar()
outVar=self.solution.get_outVar(inVar)
# 未找到换出基变量,此问题有无界解
if outVar==None:
self.status=1
return
self.solution.in_and_out(inVar,outVar)
if __name__=="__main__":
s=Simplex()
A=np.matrix([[30,20,1,0,0],
[ 5, 1,0,1,0],
[ 1, 0,0,0,1]])
b=np.matrix([[160,15,4]]).T
# sigma,...,z0
z=np.matrix([[5,2,0,0,0, 0]])
s.set_para(A,b,z)
s.output_result()
单纯形表法及其python实现
上面了说了一下单纯形的原理和程序实现,下面我们看一下单纯形表。
表格格式
设线性规划问题
$max\ z=cx\\ s.t.
\left\{ \begin{gathered}
Ax=b \hfill \\
x\geq 0 \hfill \\
\end{gathered} \right.$
其中,$A=\begin{bmatrix}1&&&&a_{1,m+1}&\cdots&a_{1,n}\\&1&&&a_{2,m+1}&\cdots&a_{2,n}\\&&\ddots&&&&\\&&&1&a_{m,m+1}&\cdots&a_{m,n} \end{bmatrix}$,$c=\begin{bmatrix}c_1&c_2&\cdots &c_n\end{bmatrix}$,
$x=\begin{bmatrix}x_1&x_2&\cdots&x_n\end{bmatrix}^T$,$B=\begin{bmatrix}b_1&b_2&\cdots&b_m\end{bmatrix}^T$。
我们建立如下表格

其中,
- (1) 第1行是价值系数,标出了决策变量$x_j$的价值系数$c_j(j=1,2,\cdots,n)$。
- (2) 第2行是标识行,标出表中主体各列的含义。
- (3) 最后1行是检验数行,除$(-z_0)$是表示当前解的目标函数$z$的负值外,其余各元素均为对应决策变量$x_j$的检验数$\sigma_j(j=0,1,\cdots,n)$(基变量的检验数为0)。
- (4) 第1列是$c_B$列,标出基变量的价值系数。
- (5) 第2列是$x_B$列,标出当前基变量的名称。
- (6) 第3列是右端项,前$m$个元素是当前基本可行解的基变量的取值。第$(m+1)$个元素是$(-z)$的取值。
- (7) 其余个列标出了约束方程组中决策变量$x_j$的系数列向量$p_j(j=0,1,\cdots,n)$(因为$z$永远不会被换出,因此表中省去了$z$的系数列)。
- (8) 最后一列留做最小比值准则求各个比值时填数据用。(最小比值准则,即选择换出基变量的准则)。
具体步骤
- (1) 检验当前基本可行解是否为最优解?
观察单纯形表的检验数行,若所有的$\sigma_j\leq 0$,则停止计算,已得到最优解,否则进行下一步。
- (2) 检验是否为无界解?
在$\sigma_j>0(j∈J_N)$,若有一个$\sigma_{m+t}>0$,而在单纯形表中$\sigma_{m+t}$所在列的其他元素,即$p_{m+t}$列的所有分量$a_{i,m+t}\leq 0(i=1,2,\cdots,m)$,则该问题无最优解,停止计算,否则进入下一步。
- (3) 选择换入基变量。
由换入基变量选择准则:$\max{\sigma_j}(\sigma_j>0,j∈J_N) = \sigma_{m+t}$,选择$x_{m+t}$为换入基变量,相应$p_{m+t}$为换入基向量。称$p_{m+t}$所在列为主列。
- (4) 选择换出基变量。
由换出基变量的最小比值准则:
$\theta=min_i\{\frac{b_i}{a_{i,m+t}}|a_{i,m+t}>0\}=\frac{b_l}{a_{l,m+t}}$
则称第$l$行为主行,与主行所对应的基变量$x_l$为换出基变量。
在求最小比值时,可将每一个比值$\frac{b_i}{a_{i,m+t}}(a_{i,m+t}>0)$纪在单纯形表的最后一列($\theta$列)的对应位置上,然后从中选出最小值。
- (5) 基变换。
将可行基由$(p_1,\cdots,p_l,\cdots,p_m)$变换为$(p_1,\cdots,p_{l-1},p_{m+t},p_{l+1},\cdots,p_m)$,且将主列$p_{m+t}$化为单位列向量$e_l$即
$p_{m+t}=\begin{bmatrix}a_{1,m+t}\\a_{2,m+t}\\ \vdots \\a_{m,m+t} \end{bmatrix} \underset{\Longrightarrow}{\ 化为\ }\ p_l=\begin{bmatrix}0\\ \vdots\\1\\ \vdots \\0\end{bmatrix}\leftarrow\ 第l个分量$
- (6) 回到(1),对新解做最优性检验。
看起来,是不是特别复杂,有没有感觉单纯表很麻烦。其实,单纯形表明确了同时大大简化了,单纯形的整个计算过程。下面以一个例子进行分析。
例子
仍然使用最开始的例子,即某问题的数学模型标准形式如下:
$\max{z}=5x_1+2x_2+0x_3+0x_4+0x_5$;
$s.t.\left \{ \begin{gathered}
30x_1+20x_2+x3=160 \hfill \\
5x_1+x_2+x_4=15 \hfill \\
x_1+x_5=4 \hfill \\
x_j\geq0,j=1,2,3,4,5 \hfill \\
\end{gathered} \right.$
解 首先,我们建立初始的单纯形表,如下
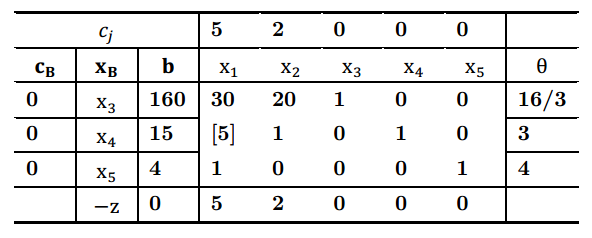
- 建表 初始可行基$B^{(0)}=(p_3,p_4,p_5)$,基变量为$x_3,x_4,x_5$,非基变量为$x_1,x_2$。
- 判优 由于$\sigma_1=5>0,\sigma_2=2>0$,故当前解不是最优解;同时判断得本题也不是无最优解问题。
- 选择换入换出基变量 由于$\sigma_1>\sigma_2$,所以选择$x_1$为换入基变量。根据最小比值准则:$\frac{160}{30},\frac{15}{5},\frac{4}{1}$,可见最小比值为3,选择$x_4$为换出基变量,$a_{2,1}$为主元素。
- 换入换出 使用初等行变换,将主元素$[5]$化为1,将主列$p_1$的其他各元素化为0,得到下表。(具体来说,首先将主元素那一行(主行)的所有元素除以5,然后主行上一行减去主行*30,主行下一行减去主行*1,此外检验数那一行减去主行*5)

- 判优 由于$\sigma_2=1>0$,故当前解不是最优解;同时判断得本题也不是无最优解问题。
- 选择换入换出基变量 由于$\sigma_2=1>0$,所以选择$x_2$为换入基变量。根据最小比值准则:$\frac{70}{14},\frac{3}{1/5}$,可见最小比值为3,选择$x_3$为换出基变量,$a_{1,2}$为主元素。
- 换入换出 使用初等行变换,将主元素$[14]$化为1,将主列$p_2$的其他各元素化为0,得到下表。

- 判优 由于所有的检验数都小于0,故当前解是最优解。因此,$z$的最大值为20,此时$x_1=2,x_2=5,x_5=2$。
python实现
import numpy as np
# 实体类 Table
# 控制类 Simplex
class Table:
def __init__(self):
pass
def set_para(self,A,b,c,base,z0):
"""
输入LP必须已经化为标准形式
"""
self.A=A
self.b=b
self.c=c
self.z0=z0
self.base=base
self.m,self.n=self.A.shape
def build(self):
self.table=np.zeros((self.m+1,self.n+1))
self.table[:-1,:1]=self.b.T
self.table[-1 ,0]=self.z0
self.table[:-1,1:]=self.A
self.table[-1, 1:]=c
self.baseVar=base
def is_best(self):
for sigma_index in range(self.n):
if sigma_index not in self.baseVar:
sigma=self.table[-1,1+sigma_index]
if sigma>0:
return False
return True
def is_no_solution(self):
for sigma_index in range(self.n):
if sigma_index not in self.baseVar:
sigma=self.table[-1,1+sigma_index]
if sigma>0:
no_solution_flag=True
for a in self.table[:-1,1+sigma_index]:
if a>0:
no_solution_flag=False
if no_solution_flag==True:
return True
return False
def get_inVar(self):
max_sigma=0
inVar=None
for sigma_index in range(self.n):
if sigma_index not in self.baseVar:
sigma=self.table[-1,1+sigma_index]
if sigma>max_sigma:
max_sigma=sigma
inVar=sigma_index
return inVar
def get_outVar(self,inVar):
rates=[]
for nobaseVar in range(self.m):
a=self.table[nobaseVar,inVar+1]
b=self.table[nobaseVar, 0 ]
if a>0:
rate=b/a
rates.append((rate,nobaseVar))
return min(rates)[1]
def in_out(self,inVar,outVar):
a=self.table[outVar,inVar+1]
self.table[outVar,:]/=a
for i in range(self.m+1):
if i != outVar:
self.table[i,:]-=self.table[outVar,:]*self.table[i,inVar+1]
self.baseVar[outVar]=inVar
def show(self):
print ('基变量/取值:',self.baseVar,end='/')
print (self.table[:-1,0])
print ("单纯形表")
for i in range(self.m+1):
for j in range(self.n+1):
print ('%6.2f'%self.table[i,j],end=' ')
print ()
print ()
class Simplex:
def __init__(self):
self.table=Table()
# 0 正常,尚未得到最优解,继续迭代
# 1 无解,无界解
# 2 达到最优解
self.status=0
self.inVar=None
self.outVar=None
def set_para(self,A,b,c,base,z0=0):
self.table.set_para(A,b,c,base,z0)
def output_result(self):
self._main()
if self.status==1:
print("此问题无界")
elif self.status==2:
print("此问题有一个最优解")
elif self.status==3:
print("此问题有无穷多个最优解")
def _main(self):
self._build_table()
while 1:
self.table.show()
if self._is_best() or self._is_no_solution():
return
self._get_inVar()
self._get_outVar()
self._in_out()
def _build_table(self):
self.table.build()
def _is_best(self):
if self.table.is_best():
self.status=2
return True
return False
def _is_no_solution(self):
if self.table.is_no_solution():
self.status=1
return True
return False
def _get_inVar(self):
self.inVar=self.table.get_inVar()
def _get_outVar(self):
self.outVar=self.table.get_outVar(self.inVar)
def _in_out(self):
self.table.in_out(self.inVar,self.outVar)
if __name__=="__main__":
s=Simplex()
A=np.matrix([[30,20,1,0,0],
[ 5, 1,0,1,0],
[ 1, 0,0,0,1]])
b=np.matrix([[160,15,4]])
c=np.matrix([[5,2,0,0,0]])
base=[2,3,4]
s.set_para(A,b,c,base)
s.output_result()
人工变量及其处理办法
需要注意的是,上面的单纯形表格法的基本假设是,输入的A中包含一个单位矩阵(也就是说,初始可行基为单位矩阵)。往往,我们需要添加人工变量来达到这个条件。例如
$A=\begin{bmatrix}30&20&1&1&2\\5&1&2&1&3\\1&2&3&4&1\\ \end{bmatrix}$,对于A这个矩阵,如果我们通过初等行变换将其转化为一个包含单位矩阵的矩阵,这是比较麻烦的;为了解决这个问题,我们通过添加人工变量$x_6,x_7,x_8$的方法,将A变成$\begin{bmatrix}30&20&1&1&2&1&&\\5&1&2&1&3&&1&\\1&2&3&4&1&&1\\ \end{bmatrix}$,这样A中就含有一个单位阵。我们可以以$x_6,x_7,x_8$为基变量,开始迭代。但是添加了人工变量后的问题与原问题已经不等价了。只有当最优解中,人工变量都取0值时,才可以认为两个问题的最优解是相当的。
为了解决这个问题,两种方法被引入。
1.大M法
假设原目标函数为$\max{z}=\sum{c_jx_j}$,添加人工变量之后,我们将目标函数修改为$\max{z}=\sum{c_jx_j}-Mx_{n+1}-Mx_{n+2}-\cdots-Mx_{n+m}$。其中,$M$是个很大的正数。为了对目标函数实现最大化,人工变量就会被迅速换出去。
2.两阶段法
当线性规划问题添加了人工变量之后,我们可以将问题拆成两个问题。
第一阶段求解第一个线性规划问题,目标函数为$\min{w}=\sum{x_{n+i}}$,即目标是对所有人工变量之和求最小。需要说明的是,当求得的最优解中,至少有一个人工变量不为0值,说明原问题无可行解,不需要继续进行第二阶段的计算。
第二阶段,目标函数为添加人工变量之前的目标函数。
1
posted on 2017-03-20 10:43 SuperZhang828 阅读(13032) 评论(2) 收藏 举报

 浙公网安备 33010602011771号
浙公网安备 33010602011771号