前言
员工离职,似乎已经成为每一家企业都要面对的问题,特别是优秀人才离职的问题会让领导特别头疼。今天我们就通过kaggle上某一家企业员工离职的真实数据来对离职率进行分析建模,并对预测结果显示要离职的员工提出挽留建议。
目录
1. 数据来源及背景
2. 明确分析目的
3. 数据探索分析
4. 数据预处理
5. 可视化分析
6. 特征工程
7. 逻辑回归模型
8. 朴素贝叶斯模型
9. 模型评估之ROC曲线
正文
1. 数据来源及背景
数据来源: https://www.kaggle.com/jiangzuo/hr-comma-sep/version/1
数据背景: 该数据集是指某公司员工的离职数据, 其包含14999个样本以及10个特征, 这10个特征分别为: 员工对公司满意度, 最新考核评估, 项目数, 平均每月工作时长, 工作年限, 是否出现工作事故, 是否离职, 过去5年是否升职, 岗位, 薪资水平.
2. 明确分析目的
该数据集讨论的是公司员工离职的问题, 那么, 我们首先需要对影响员工离职的因素进行分析:

将上述影响因素与现有的数据相结合来提出问题,进而明确我们的分析目的:
1) 员工对公司满意度平均水平如何?员工的最新考核情况又是如何?员工所参加项目数是怎样?员工平均每月工作时长以及平均工作年限分别是多少?
2) 当前离职率是多少?工作事故发生率?过去5年升职率?薪资水平又如何?共有多少种岗位?
3) 是否离职和其他9个特征的关系如何?
4) 根据现有数据, 如何对某个员工是否离职进行预测?
5) 针对当前的员工离职情况,企业该如何对待呢?
3. 数据探索分析
1) 查看前2行和后2行数据
import pandas as pd df = pd.read_csv(r'D:\Data\HR_comma_sep.csv') pd.set_option('display.max_rows', 4) df

数据维度14999行×10列, 除过岗位和薪资水平是字符型外, 其余均是数字 (具体是什么类型还需要进一步确定).
2) 查看数据类型等信息
df.info()
<class 'pandas.core.frame.DataFrame'> RangeIndex: 14999 entries, 0 to 14998 Data columns (total 10 columns): satisfaction_level 14999 non-null float64 last_evaluation 14999 non-null float64 number_project 14999 non-null int64 average_montly_hours 14999 non-null int64 time_spend_company 14999 non-null int64 Work_accident 14999 non-null int64 left 14999 non-null int64 promotion_last_5years 14999 non-null int64 sales 14999 non-null object salary 14999 non-null object dtypes: float64(2), int64(6), object(2) memory usage: 1.1+ MB
前两个特征为64位浮点型, 后两个为字符型, 其余为64位整型, 且均无缺失值.
3). 描述性统计
df.describe() df.describe(include=['O']).T

1) 员工对公司满意度平均水平如何?员工的最新考核情况又是如何?员工所参加项目数是怎样?员工平均每月工作时长以及平均工作年限分别是多少?
员工对公司的满意度: 范围 0.09~1, 中位数0.640, 均值0.613, 总体来说员工对公司较满意
最新考核评估: 范围 0.36~1, 中位数0.720, 均值0.716, 员工考核平均水平中等偏上.
项目数: 范围 2~7个, 中位数4, 均值3.8, 平均参加项目数为4个
平均每月工作时长: 范围96~310小时, 中位数200, 均值201
工作年限: 范围2~10年, 中位数3, 均值3.5
2) 当前离职率是多少?工作事故发生率?过去5年升职率?薪资水平又如何?共有多少种岗位?
当前离职率为23.81%
工作事故发生率14.46%.
过去5年升职率2.13%.

薪资水平共有3个等级, 最多的是低等, 多达7316人.
员工岗位有10种, 其中最多的是销售, 多达4140人.
4. 数据预处理
没有缺失值, 因此不用处理缺失值.
1. 异常值
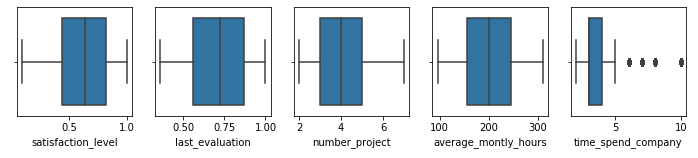
通过箱线图查看异常值.
import seaborn as sns fig, ax = plt.subplots(1,5, figsize=(12, 2)) sns.boxplot(x=df.columns[0], data=df, ax=ax[0]) sns.boxplot(x=df.columns[1], data=df, ax=ax[1]) sns.boxplot(x=df.columns[2], data=df, ax=ax[2]) sns.boxplot(x=df.columns[3], data=df, ax=ax[3]) sns.boxplot(x=df.columns[4], data=df, ax=ax[4])
除了工作年限外, 其他均无异常值. 该异常值也反映了该公司员工中以年轻人为主
5. 可视化分析
在这里通过可视化的形式对第三个问题“是否离职和其他9个特征的关系如何?”进行回答.
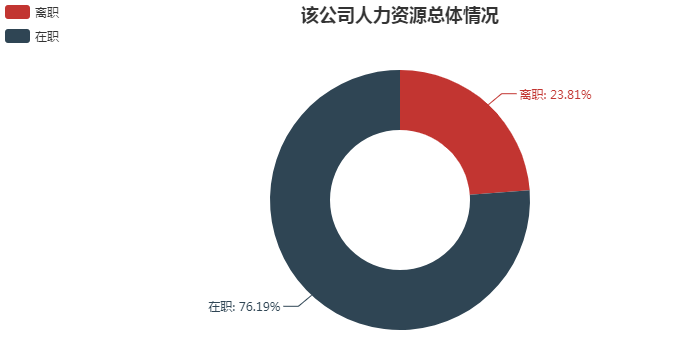
1. 人力资源总体情况
from pyecharts import Pie attr = ["离职", "在职"] v1 =[df.left.value_counts()[1], df.left.value_counts()[0]] pie = Pie("该公司人力资源总体情况", title_pos='center') pie.add( "", attr, v1, radius=[35, 65], label_text_color=None, is_label_show=True, legend_orient="vertical", legend_pos="left", ) pie.render()
离职3571人, 在职11428人, 离职率为23.81%
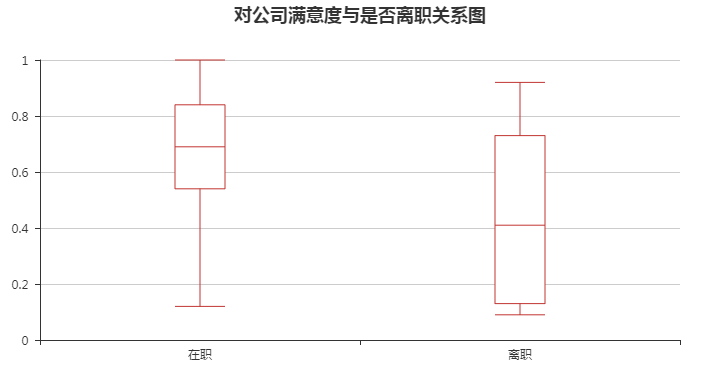
2. 对公司满意度与是否离职的关系
from pyecharts import Boxplot #字段重命名 df.columns=['satisfaction', 'evaluation', 'project', 'hours', 'years_work','work_accident', 'left', 'promotion', 'department', 'salary'] #绘制箱线图 boxplot = Boxplot("对公司满意度与是否离职关系图", title_pos='center') x_axis = ['在职', '离职'] y_axis = [df[df.left == 0].satisfaction.values, df[df.left == 1].satisfaction.values] boxplot.add("", x_axis, boxplot.prepare_data(y_axis)) boxplot.render()
就中位数而言, 离职人员对公司满意度相对较低, 且离职人员对公司满意度整体波动较大. 另外离职人员中没有满意度为1的评价.
3. 最新考核评估与是否离职的关系
boxplot = Boxplot("最新评估与是否离职关系图", title_pos='center') x_axis = ['在职', '离职'] y_axis = [df[df.left == 0].evaluation.values, df[df.left == 1].evaluation.values] boxplot.add("", x_axis, boxplot.prepare_data(y_axis)) boxplot.render()
就中位数而言, 离职人员的最新考核评估相对较高, 但其波动也大.

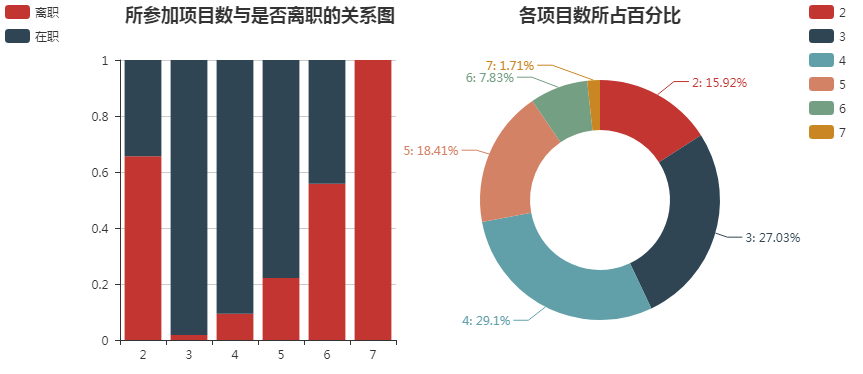
4. 所参加项目与是否离职的关系
from pyecharts import Bar, Pie, Grid #按照项目数分组分别求离职人数和所有人数 project_left_1 = df[df.left == 1].groupby('project')['left'].count() project_all = df.groupby('project')['left'].count() #分别计算离职人数和在职人数所占比例 project_left1_rate = project_left_1 / project_all project_left0_rate = 1 - project_left1_rate attr = project_left1_rate.index bar = Bar("所参加项目数与是否离职的关系图", title_pos='10%') bar.add("离职", attr, project_left1_rate, is_stack=True) bar.add("在职", attr, project_left0_rate, is_stack=True, legend_pos="left", legend_orient="vertical") #绘制圆环图 pie = Pie("各项目数所占百分比", title_pos='center') pie.add('', project_all.index, project_all, radius=[35, 60], label_text_color=None, is_label_show=True, legend_orient="vertical", legend_pos="67%") grid = Grid(width=1200) grid.add(bar, grid_right="67%") grid.add(pie) grid.render()
通过下图可以发现以下2点:
- 离职率随着项目数的增多而增大, 2个项目数是特例
- 离职率较高的项目数2, 6, 7在总项目数中所占百分比相对较少. 项目数为2的这部分人可能是工作能力不被认可, 其离职人数也相对较多; 项目数为6, 7的这部分人一方面体现的是工作能力较强, 另一方面也说明了工作强度大, 其可能在其他企业能有更好的发展, 自然离职率也相对较高.
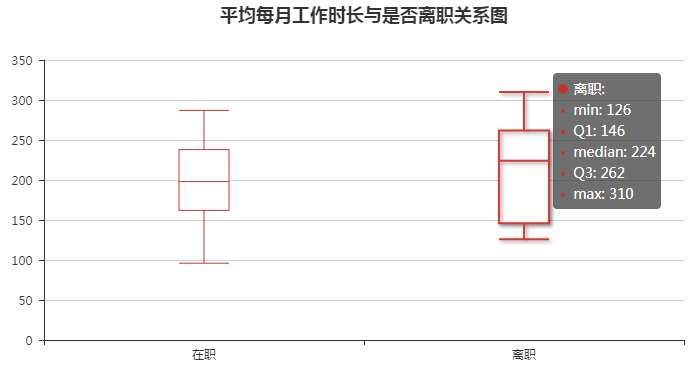
5. 平均每月工作时长和是否离职的关系
boxplot = Boxplot("平均每月工作时长与是否离职关系图", title_pos='center') x_axis = ['在职', '离职'] y_axis = [df[df.left == 0].hours.values, df[df.left == 1].hours.values] boxplot.add("", x_axis, boxplot.prepare_data(y_axis)) boxplot.render()
通过下图可以看到: 离职人员的平均每月工作时长相对较长, 每月按照22个工作日计算, 每日工作时数的中位数为10.18小时, 最大值为14.09小时.
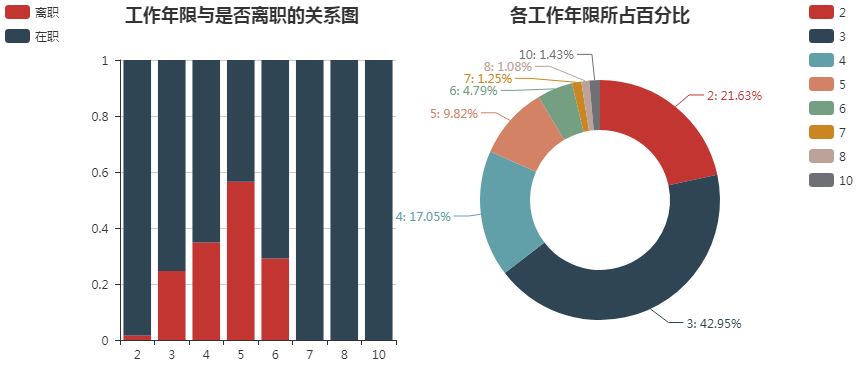
6. 工作年限和是否离职的关系
from pyecharts import Bar, Pie, Grid #按照工作年限分别求离职人数和所有人数 years_left_0 = df[df.left == 0].groupby('years_work')['left'].count() years_all = df.groupby('years_work')['left'].count() #分别计算离职人数和在职人数所占比例 years_left0_rate = years_left_0 / years_all years_left1_rate = 1 - years_left0_rate attr = years_all.index bar = Bar("工作年限与是否离职的关系图", title_pos='10%') bar.add("离职", attr, years_left1_rate, is_stack=True) bar.add("在职", attr, years_left0_rate, is_stack=True, legend_pos="left" , legend_orient="vertical") #绘制圆环图 pie = Pie("各工作年限所占百分比", title_pos='center') pie.add('', years_all.index, years_all, radius=[35, 60], label_text_color=None, is_label_show=True, legend_orient="vertical", legend_pos="67%") grid = Grid(width=1200) grid.add(bar, grid_right="67%") grid.add(pie) grid.render()
通过下图可以得出:
- 在各工作年限中, 离职人员较集中于3, 4, 5, 6年, 而6年以上则相对稳定
- 企业中工作年限为3年的人数所占百分比最多, 其次是2年, 主要以年轻人为主
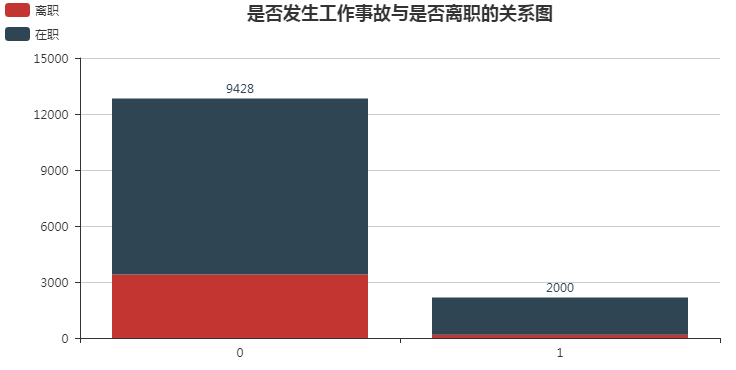
7. 是否发生工作事故与是否离职的关系
from pyecharts import Bar accident_left = pd.crosstab(df.work_accident, df.left) attr = accident_left.index bar = Bar("是否发生工作事故与是否离职的关系图", title_pos='center') bar.add("离职", attr, accident_left[1], is_stack=True) bar.add("在职", attr, accident_left[0], is_stack=True, legend_pos="left" , legend_orient="vertical", is_label_show=True) bar.render()
可以看到少部分出现工作事故, 且其中有较少部分人离职.
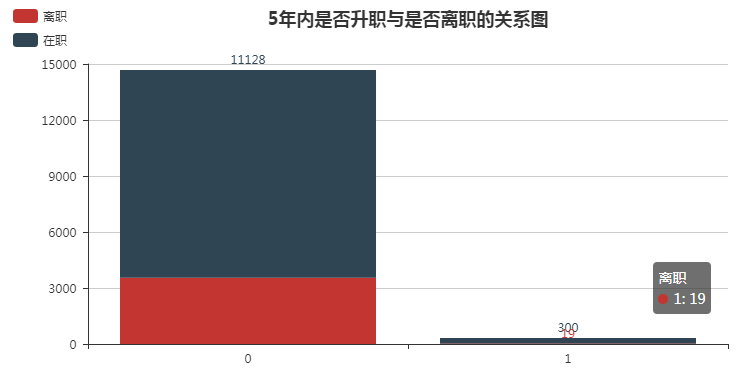
8. 5年内是否升职与是否离职的关系
promotion_left = pd.crosstab(df.promotion, df.left) attr = promotion_left.index bar = Bar("5年内是否升职与是否离职的关系图", title_pos='center') bar.add("离职", attr, promotion_left[1], is_stack=True) bar.add("在职", attr, promotion_left[0], is_stack=True, legend_pos="left" , legend_orient="vertical", is_label_show=True) bar.render()
5年内多数人没有升职, 离职率就相对较高.
9. 岗位与是否离职的关系
#分别计算各岗位离职人员比例和各岗位占总体百分比 department_left_0 = df[df.left == 0].groupby('department')['left'].count() department_all = df.groupby('department')['left'].count() department_left0_rate = department_left_0 / department_all department_left1_rate = 1 - department_left0_rate attr = department_all.index bar = Bar("岗位与离职比例的关系图", title_top='40%') bar.add("离职", attr, department_left1_rate, is_stack=True) bar.add("在职", attr, department_left0_rate, is_stack=True, is_datazoom_show=True, xaxis_interval=0, xaxis_rotate=30, legend_top="45%", legend_pos="80%") #绘制圆环图 pie = Pie("各个岗位所占百分比", title_pos='left') pie.add('', department_all.index, department_all,center=[50, 23], radius=[18, 35], label_text_color=None, is_label_show=True, legend_orient="vertical", legend_pos="80%", legend_top="4%") grid = Grid(width=1200, height=700) grid.add(bar, grid_top="50%", grid_bottom="25%") grid.add(pie) grid.render()
通过下图可以看出:
- 在所有岗位中销售岗位人数所占百分比最多, 达到27.6%, 最少是管理层, 其所占百分比是4.2%
- 令人意外的是岗位中hr离职率最高.

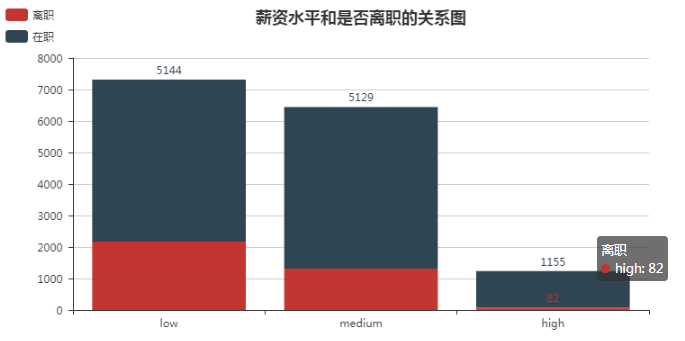
10. 薪资水平和是否离职的关系
from pyecharts import Bar #按照薪资水平分别求离职人数和所有人数 salary_left = pd.crosstab(df.salary, df.left).sort_values(0, ascending = False) attr = salary_left.index bar = Bar("薪资水平和是否离职的关系图", title_pos='center') bar.add("离职", attr, salary_left[1], is_stack=True) bar.add("在职", attr, salary_left[0], is_stack=True, legend_pos="left" , legend_orient="vertical", is_label_show=True) bar.render()
薪资分为三个水平: 低等, 中等, 高等. 低等水平离职人数最多, 所占比例也最大, 而高等则最少.
在回答第4个问题之前,需要对数据进行特征处理工作,以满足模型对数据的要求
6. 特征工程
1. 离散型数据处理
离散型数据可分为两种: 一种是定序, 一种是定类.
1) 定序
薪资水平其含有顺序意义, 因此将其字符型转化为数值型
df['salary'] = df.salary.map({"low": 0, "medium": 1, "high": 2}) df.salary.unique()
array([0, 1, 2], dtype=int64)
2) 定类
岗位是定类型变量, 对其进行one-hot编码, 这里直接利用pandas的get_dummies方法.
df_one_hot = pd.get_dummies(df, prefix="dep") df_one_hot.shape
(14999, 19)
2. 连续型数据处理
逻辑回归模型能够适应连续型变量, 因此可以不用进行离散化处理, 又由于多个特征之间差异差异较大会造成梯度下降算法收敛速度变慢, 故进行归一化处理
#采用max-min归一化方法 hours = df_one_hot['hours'] df_one_hot['hours'] = df_one_hot.hours.apply(lambda x: (x-hours.min()) / (hours.max()-hours.min()))
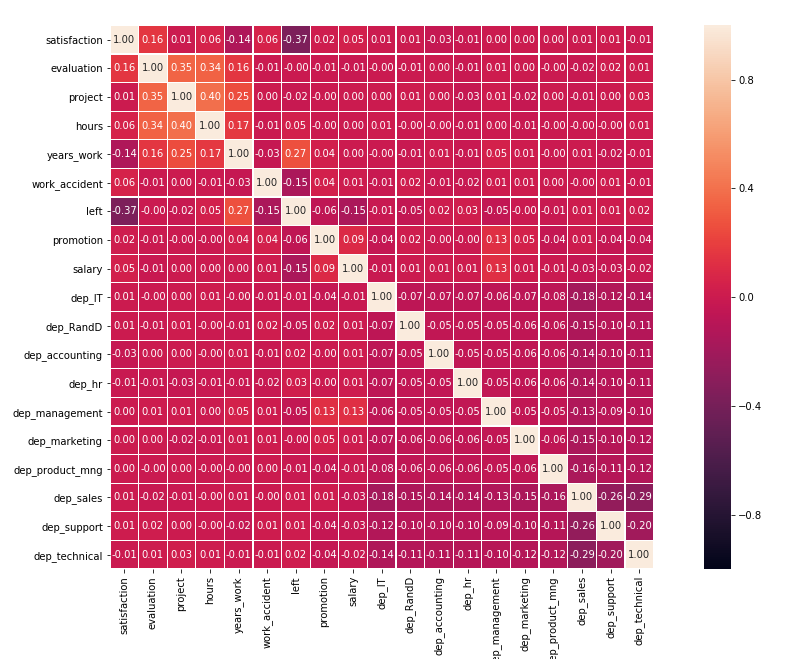
3. 相关系数
两个变量均是连续型且具有线性关系, 则可以使用皮尔逊相关系数, 否则使用斯皮尔曼相关系数, 这里采用斯皮尔曼相关系数
#计算相关系数 correlation = df_one_hot.corr(method = "spearman") plt.figure(figsize=(18, 10)) #绘制热力图 sns.heatmap(correlation, linewidths=0.2, vmax=1, vmin=-1, linecolor='w',fmt='.2f', annot=True,annot_kws={'size':10},square=True)
接下来就到了解释第四个问题的环节了, 下面将采用两种模型来对员工是否离职进行预测, 这两个模型分别是逻辑回归模型和朴素贝叶斯模型
7. 逻辑回归模型
1. 划分数据集
from sklearn.model_selection import train_test_split #划分训练集和测试集 X = df_one_hot.drop(['left'], axis=1) y = df_one_hot['left'] X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1)
2. 训练模型
from sklearn.linear_model import LogisticRegression LR = LogisticRegression() print(LR.fit(X_train, y_train)) print("训练集准确率: ", LR.score(X_train, y_train)) print("测试集准确率: ", LR.score(X_test, y_test))
LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
intercept_scaling=1, max_iter=100, multi_class='warn',
n_jobs=None, penalty='l2', random_state=None, solver='warn',
tol=0.0001, verbose=0, warm_start=False)
训练集准确率: 0.7978998249854155
测试集准确率: 0.7966666666666666
参考官方文档说明, 参数C是正则化项参数的倒数, C的数值越小, 惩罚的力度越大. penalty可选L1, L2正则化项, 默认是L2正则化.
参数solver可选{‘newton-cg’, ‘lbfgs’, ‘liblinear’, ‘sag’, ‘saga’}这5个优化算法:
newton-cg, lbfgs是拟牛顿法, liblinear是坐标轴下降法, sag, saga是随机梯度下降法, saga可以适用于L1和L2正则化项, 而sag只能用于L2正则化项.
#指定随机梯度下降优化算法 LR = LogisticRegression(solver='saga') print(LR.fit(X_train, y_train)) print("训练集准确率: ", LR.score(X_train, y_train)) print("测试集准确率: ", LR.score(X_test, y_test))
LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
intercept_scaling=1, max_iter=100, multi_class='warn',
n_jobs=None, penalty='l2', random_state=None, solver='saga',
tol=0.0001, verbose=0, warm_start=False)
训练集准确率: 0.7980665055421285
测试集准确率: 0.7973333333333333
在选择随机梯度下降法后, 训练集和测试集准确率均略有提升.
3. 调参
#用准确率进行10折交叉验证选择合适的参数C from sklearn.linear_model import LogisticRegressionCV Cs = 10**np.linspace(-10, 10, 400) lr_cv = LogisticRegressionCV(Cs=Cs, cv=10, penalty='l2', solver='saga', max_iter=10000, scoring='accuracy') lr_cv.fit(X_train, y_train) lr_cv.C_
array([25.52908068])
用该参数进行预测
LR = LogisticRegression(solver='saga', penalty='l2', C=25.52908068) print("训练集准确率: ", LR.score(X_train, y_train)) print("测试集准确率: ", LR.score(X_test, y_test))
训练集准确率: 0.7984832069339112 测试集准确率: 0.798
训练集和测试集准确率均有所提升, 对于二分类问题, 准确率有时不是很好的评估方法, 这时需要用到混淆矩阵
4. 混淆矩阵
from sklearn import metrics X_train_pred = LR.predict(X_train) X_test_pred = LR.predict(X_test) print('训练集混淆矩阵:') print(metrics.confusion_matrix(y_train, X_train_pred)) print('测试集混淆矩阵:') print(metrics.confusion_matrix(y_test, X_test_pred))
训练集混淆矩阵: [[8494 647] [1771 1087]] 测试集混淆矩阵: [[2112 175] [ 431 282]]
from sklearn.metrics import classification_report print('训练集:') print(classification_report(y_train, X_train_pred)) print('测试集:') print(classification_report(y_test, X_test_pred))
训练集:
precision recall f1-score support
0 0.83 0.93 0.88 9141
1 0.63 0.38 0.47 2858
micro avg 0.80 0.80 0.80 11999
macro avg 0.73 0.65 0.67 11999
weighted avg 0.78 0.80 0.78 11999
测试集:
precision recall f1-score support
0 0.83 0.92 0.87 2287
1 0.62 0.40 0.48 713
micro avg 0.80 0.80 0.80 3000
macro avg 0.72 0.66 0.68 3000
weighted avg 0.78 0.80 0.78 3000
在训练集有0.83的精准率和0.93的召回率, 在测试集上有0.83的精准率和0.92的召回率.
8. 朴素贝叶斯模型
朴素贝叶斯模型是基于特征条件独立假设和贝叶斯理论.
from sklearn.naive_bayes import GaussianNB from sklearn.model_selection import cross_val_score #构建高斯朴素贝叶斯模型 gnb = GaussianNB() gnb.fit(X_train, y_train) print("训练集准确率: ", gnb.score(X_train, y_train)) print("测试集准确率: ", gnb.score(X_test, y_test)) X_train_pred =gnb.predict(X_train) X_test_pred = gnb.predict(X_test) print('训练集混淆矩阵:') print(metrics.confusion_matrix(y_train, X_train_pred)) print('测试集混淆矩阵:') print(metrics.confusion_matrix(y_test, X_test_pred)) print('训练集:') print(classification_report(y_train, X_train_pred)) print('测试集:') print(classification_report(y_test, X_test_pred))
训练集准确率: 0.7440620051670973
测试集准确率: 0.741
训练集混淆矩阵:
[[6791 2350]
[ 721 2137]]
测试集混淆矩阵:
[[1680 607]
[ 170 543]]
训练集:
precision recall f1-score support
0 0.90 0.74 0.82 9141
1 0.48 0.75 0.58 2858
micro avg 0.74 0.74 0.74 11999
macro avg 0.69 0.75 0.70 11999
weighted avg 0.80 0.74 0.76 11999
测试集:
precision recall f1-score support
0 0.91 0.73 0.81 2287
1 0.47 0.76 0.58 713
micro avg 0.74 0.74 0.74 3000
macro avg 0.69 0.75 0.70 3000
weighted avg 0.80 0.74 0.76 3000
可以看到其准确率较逻辑回归低, 但是精准率高于逻辑回归.
9. 模型评估之ROC曲线
from sklearn import metrics from sklearn.metrics import roc_curve #将逻辑回归模型和高斯朴素贝叶斯模型预测出的概率均与实际值通过roc_curve比较返回假正率, 真正率, 阈值 lr_fpr, lr_tpr, lr_thresholds = roc_curve(y_test, LR.predict_proba(X_test)[:,1]) gnb_fpr, gnb_tpr, gnb_thresholds = roc_curve(y_test, gnb.predict_proba(X_test)[:,1]) #分别计算这两个模型的auc的值, auc值就是roc曲线下的面积 lr_roc_auc = metrics.auc(lr_fpr, lr_tpr) gnb_roc_auc = metrics.auc(gnb_fpr, gnb_tpr) plt.figure(figsize=(8, 5)) plt.plot([0, 1], [0, 1],'--', color='r') plt.plot(lr_fpr, lr_tpr, label='LogisticRegression(area = %0.2f)' % lr_roc_auc) plt.plot(gnb_fpr, gnb_tpr, label='GaussianNB(area = %0.2f)' % gnb_roc_auc) plt.xlim([0.0, 1.0]) plt.ylim([0.0, 1.0]) plt.title('ROC') plt.xlabel('FPR') plt.ylabel('TPR') plt.legend() plt.show()
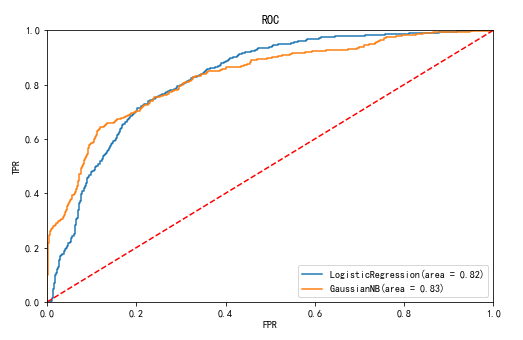
ROC曲线越靠近左上角说明分类效果越好, 与之对应的auc的值就越大. 对于该数据集来说, 高斯朴素贝叶斯模型略优于逻辑回归模型
以上就是对第四题的解释, 下面进入第五题
5) 针对当前的员工离职情况,企业该如何对待呢?
该公司的员工离职现状:
1.当前离职率为23.81%
2.离职人员对公司满意度普遍较低
3.离职人员的考核成绩相对较高, 说明离职人员多数为优秀人才.
4.项目数范围为2~7个, 其中参加7个项目的离职率最高,其次是2个的; 7个的工作能力较强, 在其他企业有更好的发展, 2个的可能是在该公司中工作能力不被认可
5.离职人员的平均每月工作时长较长
6.离职人员的工作年限集中在3到6年
7.5年内未升职的离职率较高
8.hr岗位的离职率最高, 目前企业普遍存在"留人难, 招人难”,这可能是导致该岗位的离职率高的主要原因
9.低等薪资水平的离职率最高
由于企业培养人才是需要大量的成本, 为了防止人才再次流失, 因此应当注重解决人才的流失问题, 也就是留人, 另外如果在招人时注意某些问题, 也能在一定程度上减少人才流失. 因此, 这里可将对策分为两种, 一种是留人对策, 一种是招人对策.
留人对策:
1.建立良好的薪酬制度, 不得低于市场水平
2.建立明朗的晋升机制
3.完善奖惩机制, 能者多劳, 也应多得.
4.实现福利多样化, 增加员工对企业的忠诚度
5.重视企业文化建设, 树立共同的价值观
6.改善办公环境以及营造良好的工作氛围
7.鼓励员工自我提升
招人对策:
1.明确企业招聘需求, 员工的能力应当与岗位需求相匹配
2.与应聘者坦诚相见
3.招聘期间给予的相关承诺必须实现
4.欢迎优秀流失人才回归
总结
本文从逻辑回归模型的原理开始介绍, 并通过实际案例对逻辑回归模型进行应用, 但是结果还不是很好, 一方面是模型表现不是很好(当然, 也仅仅用到了逻辑回归和朴素贝叶斯) ; 另一方面是特征工程没有处理好(朴素贝叶斯模型对特征条件独立假设较敏感), 应当进行特征选择, 比如主成分分析.
参考资料:
网易云课堂《吴恩达机器学习》
《Python数据分析与挖掘实战》
以上便是我本次分享的内容,如有任何疑问,请在下方留言,或在公众号【转行学数据分析】联系我!!!


