n=m1+m2+...+mi; (其中mi为正整数,并且1 <= mi <= n),则{m1,m2,...,mi}为n的一个划分。
如果{m1,m2,...,mi}中的最大值不超过m,即max(m1,m2,...,mi)<=m,则称它属于n的一个m划分。这里我们记n的m划分的个数为f(n,m);
例如但n=4时,他有5个划分,{4},{3,1},{2,2},{2,1,1},{1,1,1,1};
注意4=1+3 和 4=3+1被认为是同一个划分。
该问题是求出n的所有划分个数,即f(n, n)。下面我们考虑求f(n,m)的方法;
根据n和m的关系,考虑以下几种情况:
(1)当n=1时,不论m的值为多少(m>0),只有一种划分即{1};
(2)当m=1时,不论n的值为多少,只有一种划分即n个1,{1,1,1,...,1};
(3)当n=m时,根据划分中是否包含n,可以分为两种情况:
(a)划分中包含n的情况,只有一个即{n};
(b)划分中不包含n的情况,这时划分中最大的数字也一定比n小,即n的所有(n-1)划分。
因此 f(n,n) =1 + f(n,n-1);
(4)当n<m时,由于划分中不可能出现负数,因此就相当于f(n,n);
(5)但n>m时,根据划分中是否包含最大值m,可以分为两种情况:
(a)划分中包含m的情况,即{m, {x1,x2,...xi}}, 其中{x1,x2,... xi} 的和为n-m,可能再次出现m,因此是(n-m)的m划分,因此这种划分个数为f(n-m, m);
(b)划分中不包含m的情况,则划分中所有值都比m小,即n的(m-1)划分,个数为f(n,m-1);
因此 f(n, m) = f(n-m, m)+f(n,m-1);
综合以上情况,我们可以看出,上面的结论具有递归定义特征,其中(1)和(2)属于回归条件,(3)和(4)属于特殊情况,将会转换为情况(5)。而情况(5)为通用情况,属于递推的方法,其本质主要是通过减小m以达到回归条件,从而解决问题。其递推表达式如下: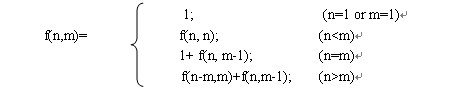
源码如下:




