P4147 玉蟾宫--单调栈

P4147 玉蟾宫

 

题目背景

 

有一天，小猫rainbow和freda来到了湘西张家界的天门山玉蟾宫，玉蟾宫宫主蓝兔盛情地款待了它们，并赐予它们一片土地。

 

题目描述

 

这片土地被分成N*M个格子，每个格子里写着'R'或者'F'，R代表这块土地被赐予了rainbow，F代表这块土地被赐予了freda。

 

现在freda要在这里卖萌。。。它要找一块矩形土地，要求这片土地都标着'F'并且面积最大。

 

但是rainbow和freda的OI水平都弱爆了，找不出这块土地，而蓝兔也想看freda卖萌（她显然是不会编程的……），所以它们决定，如果你找到的土地面积为S，它们每人给你S两银子。

 

输入输出格式

输入格式：

 

 

第一行两个整数N,M，表示矩形土地有N行M列。

 

接下来N行，每行M个用空格隔开的字符'F'或'R'，描述了矩形土地。

 

 

输出格式：

 

 

输出一个整数，表示你能得到多少银子，即(3*最大'F'矩形土地面积)的值。

 

 

 

输入输出样例

 

输入样例#1： 

5 6 
R F F F F F 
F F F F F F 
R R R F F F 
F F F F F F 
F F F F F F

输出样例#1： 

45

 

这是一道非常经典的题目。看到学长们个个都用悬线法来做，无奈本蒟蒻水平过低，只会用单调栈来切这道题。

 

我们可以把F看做1，R看做0。

来看下面这个矩阵：

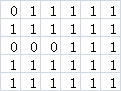
看起来这道题似乎无从下手，但是如果我们把每一列1的连续和求出来，像这样：

也许我们仍然没能发现什么规律，但是不要紧，我们接着看：

              

       

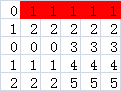
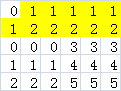
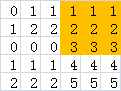
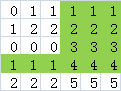
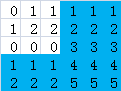
我们尝试以每一行作为这个矩形的底边，找出图中最大的矩形，也就是图中的染色部分，有没有想起点什么？

 这不就是poj 2559 Largest Rectangle in a Histogram 这道题吗？这样我们的思路也就得出了，我们可以先对读入的数据预处理一下，统计每一列的连续和，然后对每一行维护一个单调栈，求出以每一行为底的最大矩阵的大小，最后取最大值。

#include<stack>
#include<cstdio>
#include<string>
#include<cstring>
#include<queue>
#include<cmath>
#include<algorithm>
#include<map>
#include<iostream>
#define maxn 1005
using namespace std;

stack<int>s;

inline int read()
{
    char c=getchar();
    int res=0,x=1;
    while(c<'0'||c>'9')
    {
        if(c=='-')
        x=-1;
        c=getchar();
    }
    while(c>='0'&&c<='9')
    {
        res=res*10+(c-'0');
        c=getchar();
    }
    return x*res;
}

long long ans;
int n,m,a[maxn],w[maxn];
int ju[maxn][maxn];
char aa;

int main()
{
    n=read();m=read();
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            scanf("%s",&aa);
            if(aa=='F')
            {
                ju[i][j]=1;
            }
            if(aa=='R')
            {
                ju[i][j]=0;
            }
        }
    }
    for(int j=1;j<=m;j++)
    {
        for(int i=1;i<=n;i++)
        {
             if(ju[i][j]==1)
             {
                 ju[i][j]=ju[i-1][j]+1;
            }
            else
            {
                ju[i][j]=0;
            }
        }
    }
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            a[j]=ju[i][j];
        }
        a[1+m]=0;
        while(s.size()) s.pop();
        for(int j=1;j<=m+1;j++)
        {
            if(s.empty()||a[j]>=s.top())
            {
                s.push(a[j]);
                w[s.size()]=1;
            }
            else
            {
                int mi=0;
                while(!s.empty()&&a[j]<s.top())
                {
                    mi+=w[s.size()];
                    ans=max(ans,(long long)mi*s.top());
                    s.pop();
                }
                s.push(a[j]);
                w[s.size()]=mi+1;
            }
        }
    }
    printf("%lld\n",ans*3);
    return 0;
}