C/C++ 数据结构堆排序算法的实现

1.堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法，它是选择排序的一种。可以利用数组的特

点快速定位指定索引的元素。

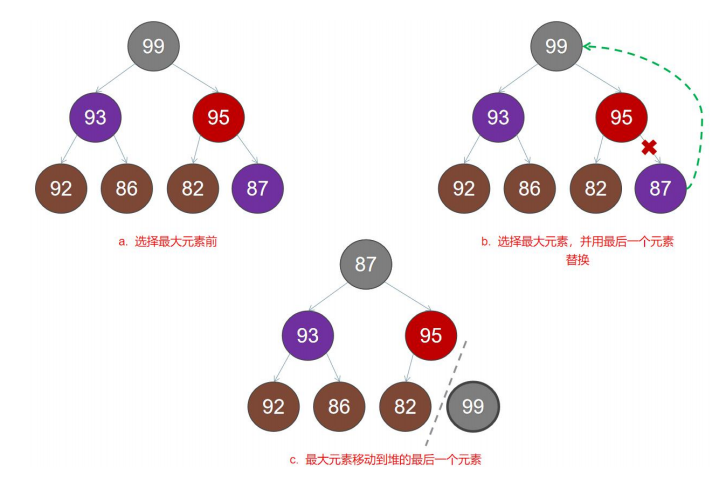
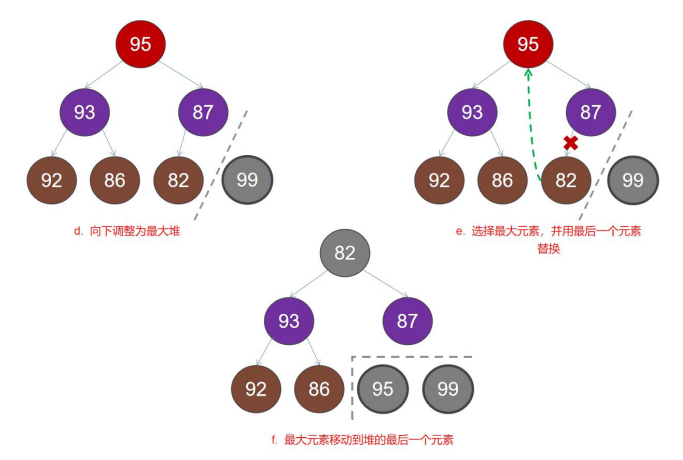
2.(选择排序工作原理 - 第一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，

然后再从剩余的未排序元素中寻找到最小（大）元素，然后放到已排序的序列的末尾。以此类推，直到全部待

排序的数据元素的个数为零)

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
typedef struct _Heap {
    int* arr; //存储堆元素的数组
    int size; //当前已存储的元素个数
    int capacity; //当前存储的容量
}Heap;
bool initHeap(Heap& heap, int* orginal, int size);
bool popMax(Heap& heap, int& value);
void heapSort(Heap& heap);
static void buildHeap(Heap& heap);
static void adjustDown(Heap& heap, int index);
/*初始化堆*/
bool initHeap(Heap& heap, int* orginal, int size) {
    //heap.arr = new int[capacity];
    heap.arr = orginal;
    if (!heap.arr) return false;
    heap.capacity = size;
    heap.size = size;
    //如果存在原始数据则构建堆
    if (size > 0) {
        //方式一: 直接调整所有元素
        //建堆
        buildHeap(heap);
    }
    return true;
}
/* 从最后一个父节点(size/2-1 的位置)逐个往前调整所有父节点（直到根节
点）, 确保每一个父节点都是一个最大堆，最后整体上形成一个最大堆 */
void buildHeap(Heap& heap) {
    int i;
    for (i = heap.size / 2 - 1; i >= 0; i--) {
        adjustDown(heap, i);
    }
}
/*将当前的节点和子节点调整成最大堆*/
void adjustDown(Heap& heap, int index)
{
    int cur = heap.arr[index];//当前待调整的节点
    int parent, child;
    /*判断否存在大于当前节点子节点，如果不存在 ，则堆本身是平衡的，不
    需要调整；
    如果存在，则将最大的子节点与之交换，交换后，如果这个子节点还有子节
    点，则要继续
    按照同样的步骤对这个子节点进行调整
    */
    for (parent = index; (parent * 2 + 1) < heap.size; parent = child) {
        child = parent * 2 + 1;
        //取两个子节点中的最大的节点
        if (((child + 1) < heap.size) && (heap.arr[child] < heap.arr[child +
            1])) {
            child++;
        }
        //判断最大的节点是否大于当前的父节点
        if (cur >= heap.arr[child]) {//不大于，则不需要调整，跳出循环
            break;
        }
        else {//大于当前的父节点，进行交换，然后从子节点位置继续向下调整
            heap.arr[parent] = heap.arr[child];
            heap.arr[child] = cur;
        }
    }
}
/* 实现堆排序 */
void heapSort(Heap& heap) {
    if (heap.size < 1) return;
    while (heap.size > 0) {
        int tmp = heap.arr[0];
        heap.arr[0] = heap.arr[heap.size - 1];
        heap.arr[heap.size - 1] = tmp;
        heap.size--;
        adjustDown(heap, 0);// 向下执行堆调整
    }
}int main(void) {
    Heap hp;
    int origVals[] = { 1, 2, 3, 87, 93, 82, 92, 86, 95 };
    int i = 0;
    if (!initHeap(hp, origVals, sizeof(origVals) / sizeof(origVals[0]))) {
        fprintf(stderr, "初始化堆失败！\n");
        exit(-1);
    }
    for (i = 0; i < hp.size; i++) {
        printf("the %dth element:%d\n", i, hp.arr[i]);
    }
    //执行堆排序
    heapSort(hp);
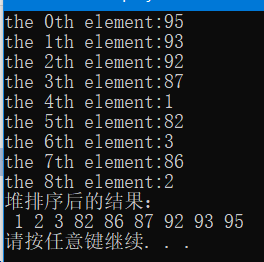
    printf("堆排序后的结果：\n");
    for (i = 0; i < sizeof(origVals) / sizeof(origVals[0]); i++) {
        printf(" %d", origVals[i]);
    }
    printf("\n");
    system("pause");
    return 0;
}