机器学习之条件随机场

　　CRF是一种灵活的框架，它包含了用于视觉识别的各种各样的特征，特别的，CRF被用于学习低级（颜色和边缘）线索的最佳组合和预学习高级模块（基于部件检测器，bag-of-words分类器）对特定视觉识别问题（eg.图像分割）中图像模型提供推理功能。

　　学习条件随机场之前，需要了解概率图模型的相关知识。

　　概率图模型

　　概率图模型是一类用图结构表达各属性之间相关关系的概率模型，一般的，图中的一个结点表示一个或一组随机变量，结点之间的边则表示变量间的相关关系，从而形成了一张‘变量关系图’。若使用有向的边来表达变量之间的依赖关系，这样的关系图称为贝叶斯网或有向图模型，若使用无向边，则称为马尔科夫网或无向图模型

　　1.隐马尔可夫模型（HMM）

　　隐马尔可夫模型（hidden Markov Model,HMM）是结构最简单的一种贝叶斯网，主要用于时序数据建模，在语音识别和自然语言处理上有着广泛的应用。在HMM中变量分为两组，观测变量和状态变量（隐变量），状态变量一般未知，比如在高斯模型中，某一种样本的分布是参数为多少的高斯模型，这个参数就是隐变量。观测变量是可以观测到的值，一般为已知的输出值。在隐马尔可夫模型中，变量之间的依赖关系遵循以下规则：

　　1）在任一时刻，观测变量的取值仅依赖于状态变量，即xt由yt确定，与其他状态变量及观测变量的取值无关。

 　   2）t时刻的y_t仅依赖于t-1时刻的状态y_t-1，与前t-2个个状态无关，这就是马尔可夫链，即：系统下一时刻的状态仅由当前状态决定，不依赖于以往的任何状态。

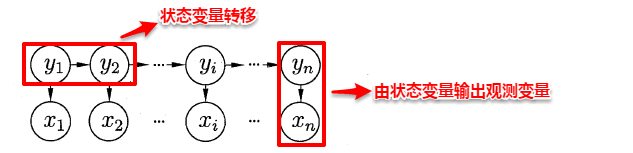
　　                                                                            y1,y2...yn表示状态变量，x1,x2..xn表示观测变量

　　基于上述的依赖关系，隐马尔可夫模型中所有变量的联合概率如下：

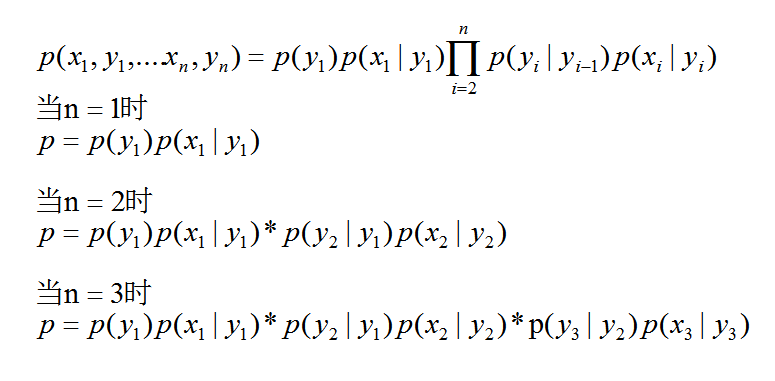
　　状态变量与它的前一个变量有直接的关系。状态变量的取值存在一个概率值，在此状态变量的条件下观测变量的取值也存在一个概率值

　　容易看出，想要确定一个HMM模型需要以下参数：

　　1）状态转移概率矩阵：从当前状态转移到下一个状态的概率矩阵，通常记为A=[a_ij]_N*N：

　              

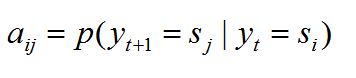
　　　　表示在任意时刻t，若状态为s_i，则在下一时刻为s_j的概率

　　2）根据状态输出观测值概率矩阵，通常记为B=[b_ij]_N*M：

　　　　

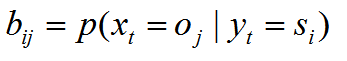
 　　b_ij表示在任意时刻t，若状态为s_i，则观测值o_j被获取的概率

　　3）初始状态概率，模型在初始时刻各状态出现的概率，通常记为π=（π₁，π₂,...,π_N）：

　　       π_i = p（y₁=s_i）

　　　　表示模型的初始状态为s_i的概率。

当确定了一个HMM模型的状态空间，观测空间，初始状态概率后，便按照下面的规则生成观测值序列：

　　（1）设置t=1,并根据初始状态概率π选择初始状态y₁，（根据初始状态概率向量）

　　（2）根据状态y_t和输出观测概率B选择观测变量取值x_t，（由状态产生观测值）

　　（3）根据状态y_t和状态转移矩阵A转移模型状态，即确定y_t+1，（状态转移概率矩阵）

　　（4）若t<n,（n表示状态数或者观测变量的数目），设置t=t+1，并转到第（2）步，否则停止

其中 y_t∈{s₁,s₂,..,s_N} 和 x_t∈{o₁,o₂,...,o_M}分别为第t时刻的状态和观测值

　　在实际应用中，HMM模型常被关注的三个问题：

　　（1）给定模型 λ=[A,B,π]，如何有效计算其产生观测序列x={x₁,x₂,...,x_n}的概率P(x|λ)，或者说，如何评价模型与观测序列之间的匹配程度？

　　（2）给定模型 λ=[A,B,π]和观测序列 x={x₁,x₂,...,x_n},如何找到与此观测序列最匹配的状态序列 y={y₁,y₂,...,y_n},或者说，如何根据观测序列推断出隐藏的模型状态。

　　（3）给定观测序列 x={x1,x2,...,xn},如何调整模型参数 λ=[A,B,π]使得该序列出现的概率p(x|λ)最大，或者说，如何训练模型是其最好的描述观测数据（EM算法：期望值最大算法，使用最大似然估计）

　　1.1 HMM评估

　　HMM评估问题指的是：给定了模型的三个参数与观测值序列，求该观测值序列出现的概率。例如：对于赌场问题可以根据骰子掷出的结果序列来计算该结果序列出现的可能性，若小概率事件发生了，则可认为赌场的骰子有作弊的可能。解决该问题使用的前向算法（步步为营，自底向上的方式逐步增加序列的长度，直到获得目标概率值），在前向算法中，定义了一个前向变量，即给定观察者序列且t时刻的状态为s_i的概率：

 

 

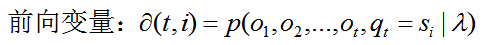
 　　递推关系和终止条件如下：

　　（个人理解）在递推关系中，a为状态转移矩阵，a(i,j):从s_i这个状态到s_j这个状态，表示给定的观察者序列且t时刻的状态为s_i的概率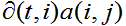，是一个联合概率，表示t时刻为s_i的概率乘上转移到下一个状态的概率，但是在前向变量里面还包含着一个观察者序列。求和表示把前j个状态的概率值加起来，最后乘上观测值概率（在第j个状态下，观测值的概率），最终结作为第t+1个时刻的前向变量。 

　　终止条件：到达最后的一个状态变量或者观测变量。

　　根据以上思路，可以使用动态规划法，从最小的子问题开始，通过填表格的形式一步步的计算目标结果。

　　1.2 HMM解码问题

　　HMM解码问题指的是：给定模型的三个参数与观测值序列，求可能性最大的状态序列。如，在语音识别问题中，人说话形成的数字信号对应着观测值序列，对应的具体文字则是状态序列，从数字信号转化为文字正是对应着根据观测值序列推断最有可能的状态序列。（解决该问题使用的是Viterbi算法，与前向算法十分类似，Viterbi算法定义了一个Viterbi变量，也是采用动态规划的方法，自底向上逐步求解。）

　　Viterbi算法公式：

 

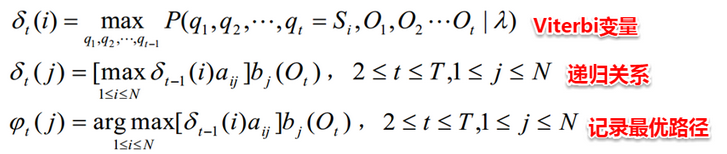
 　　1.3 HMM学习问题

　　HMM学习问题指的是：给定观测值序列，如何调整模型的参数使得该序列出现的概率最大。这便转化为机器学习问题，即从给定的序列中学习出一个HMM模型，这也正是EM算法的经典案例之一（在EM算法中采用的是最大似然估计）。其思想为：对于给定的观测值序列，如果我们能够按照序列潜在的规律来调整模型的三个参数，则可以使得该序列出现的可能性最大。假设状态序列已知，则很容易计算出该序列最契合的模型参数：

 　　公式的个人理解：

　　　　（1）：状态1到其他状态的值，根据x=y,等于1，否则等于0，这种规则确定的

                                                            

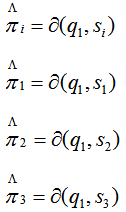
　　　　（2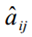）：a_ij表示状态转移概率矩阵，而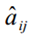仍表示状态转移矩阵

 

 

 

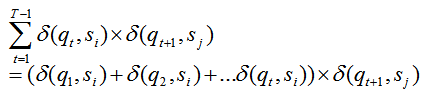
　　　　（3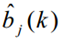）：Q中由状态q_j输出v_k的次数/Q到q_j的次数

 

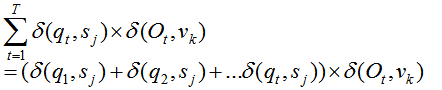
　　但一般状态值序列都是不可观测的，且即使给定观测值序列与模型参数，状态序列仍热遭遇组合爆炸。，因此上面的统计方法行不通，状态值序列看作为隐变量，这时便可以考虑使用EM算法来对该问题进行求解：（将序列拆分为两段）

　　（1）首先对HMM模型的三个参数进行随机初始化

　　（2）根据模型的参数与观测值序列，计算t时刻状态为i且t+1时刻状态为j的概率以及t时刻状态为i的概率。

 

 

 

 

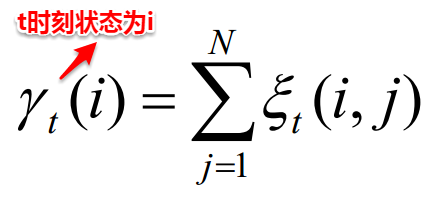
 　　（3）接着便可以对模型的三个参数进行重新估计：

 

 

 　　（4） 重复步骤2-3，直至三个参数值收敛，使得到了最终的HMM模型

 　　2 马尔可夫随机场（MRF）

　　马尔可夫随机场是是典型的马尔可夫网，是一种著名的无向图模型，图中的每个结点都表示一个或一组变量，结点之间的边表示两个向量之间的依赖关系。马尔可夫随机场有一组势函数，也称因子，这是定义在变量子集上的非负实函数，主要用于定义概率分布函数。

　　马尔可夫随机场：对于图中结点一个子集，若其中任意两结点间都有边连接，则称该结点子集为一个团，若在一个团中，加入另外任何一个结点都不再形成团，则称该团为极大团，换言之，极大团就是不能被其他团所包含的团。

　　在马尔可夫随机场中，多个变量之间的联合概率分布能基于团分解为多个因子的乘积，每个因子仅与一个团相关。具体来说，对于n个变量x={x₁,x₂,...,x_n},所有团构成的集合为C，与团Q∈C对应的变量集合记为x_Q,则联合概率P（x）定义为

　　

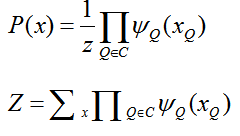
　　x(Q)为变量的集合，φ（Q）为与团Q对应的势函数，用于对团Q中的变量关系进行建模，是定义概率分布的函数，Z表示规范化因子，以确保P(x)是被正确定义的概率，在实际中，计算Z比较困难，但许多任务中不需获得Z的精确值。

　　例如，以下图是一个简单的马尔可夫随机场：

 

 

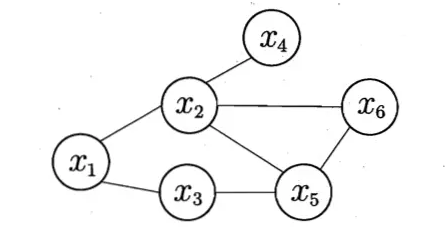
 　　极大团：{x₁,x₂},{x₂,x₅,x₆},{x₂,x₄},{x₁,x₃},{x₃,x₅},联合概率P(x)定义为：

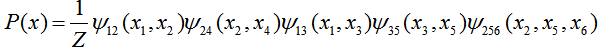
 note:势函数φ₂₅₆（x₂,x₅,x₆）定义在极大团{x₂,x₅,x₆}上，由于它的存在，使我们不需再为团{x₂,x₅},{x₂,x₆},{x₅,x₆}构建势函数。

　　在马尔可夫随机场中，如何得到条件独立性呢，借助分离的概念，如下图，若从结点集A的结点到结点集B的结点，则必须经过结点集C中的结点，则称结点集A和B被结点集C分离，C称为分离集，对马尔可夫随机场，有：

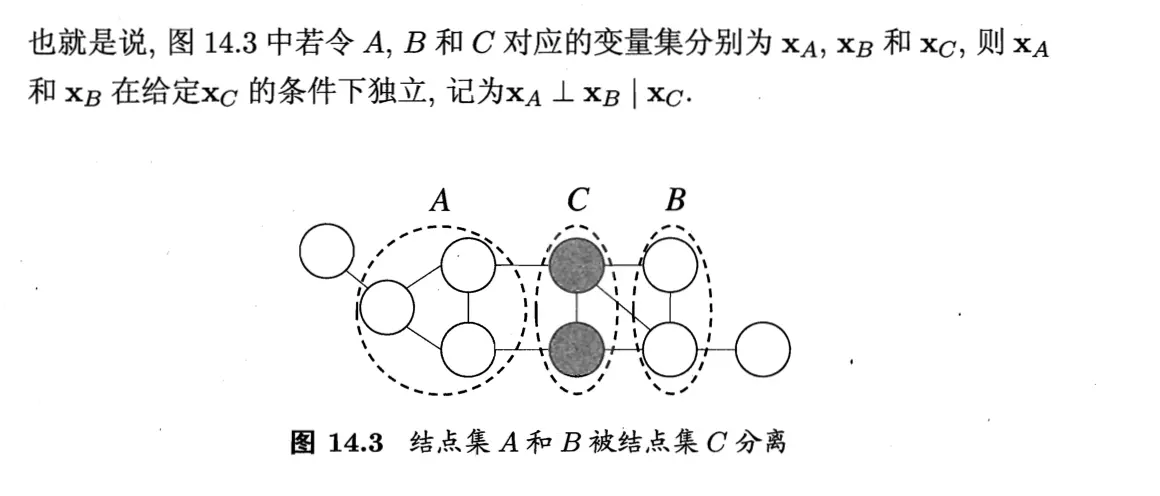
 　　全局马尔可夫性：给定两个变量子集的分离集，则这两个变量子集条件独立。

 

 

 　　局部马尔可夫性：给定某变量的邻接变量，则该变量与其他变量条件独立。

　　形式化表示：令V为图的结点集，n(v)为结点v在图上的邻接点，n*(v)=n(v)∪{v},有x_v⊥x_V\n*(v)|x_n(v),  x_v\n*(v)表示结点中除去n*(v),这个结点。eg，在图14.4中:x_a的邻接变量为x_c，则x_a与x_b在x_c的条件下独立

 　　成对马尔可夫性：给定所有其他变量，两个非邻接变量条件独立

　　形式化表示：令图中的结点集和边集分别为V和E，对图中的两个结点u和v,若<u，v>∉E，则x_u⊥x_v|x_V\<u,v>,x_V\<u,v>表示除去u和v之外的其他顶点

　　 3 条件随机场（CRF）

 　　隐马尔可夫模型和马尔可夫随机场都属于生成式模型（对联合概率进行建模），条件随机场则是对条件分布进行建模。CRF试图对多个变量在给定观测值序列后的条件概率进行建模，若x={x1,x2,...,xn}为观测序列，y ={y1,y2,...,yn}为与之相应的标记序列，则条件随机场的目标是构建条件概率模型即 P(y|x)，标记变量y可以上结构型变量，即分量之间具有某种相关性。eg 在自然语言处理的词性标注任务中，观测序列为语句（即单词序列），标记为相应的词性序列，具有线性序列结构，如下图（a），在语法分析任务中，输出标记则是语法树，具有树形结构，如下图（b）。

 

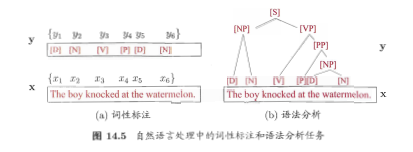
　　令图 G=<V,E>表示结点与标记变量y中元素一一对应的无向图，y_v表示与结点V对应的标记变量，n（v）表示结点v的邻接结点。若图中的每个结点y_v都满足马尔可夫性，即

 

 则（y，x）构成一个条件随机场。

　　图G可具有任意结构，在实际应用中，尤其对标记序列建模时，最常用的仍是如下图的链式结构，即链式条件随机场（chain-structured CRF）,下图是我们常用的链式条件随机场，其主要包含两种关于标记变量的团，即单个标记变量{y_i}以及相邻的标记变量{y_i-1,y_i}，与马尔可夫随机场定义联合概率类似，CRF也通过团以及势函数的概念来定义条件概率P（y|x）

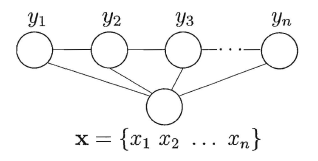
 　　通过引入两类特征函数便可以定义出目标条件概率：

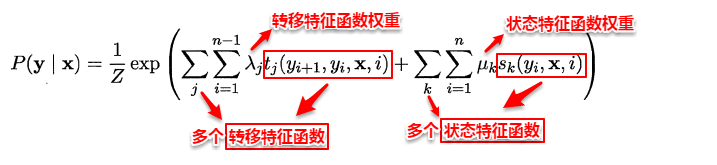
 公式解读：

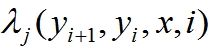　　　表示定义在观测序列的两个相邻标记位置上的转移特征函数，用于刻画相邻标记变量之间的相关关系以及观测序列对他们的影响，

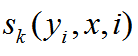 　　表示在观测序列的标记位置i上的状态特征函数，用于刻画观测序列对标记变量的影响，λ_j和u_k为参数，z为规范因子。

　　例如，词性标注：如何判断给出的标注序列靠谱不靠谱，转移特征函数主要判定两个相邻的标注是否合理，例如，动词+动词语法不通，状态特征函数判定观测值与对应的标注是否合理，例如：ly结尾的词-->副词较合理。因此我们可以定义一个特征函数集合，用这个特征函数集合来为一个标准序列打分，根据此选出靠谱的标注序列。每一个特征函数都可以用来为一个标准序列评分，把集合中所有特征函数对同一个标注序列的评分综合起来，就是这个标注序列最终的评分值。特征函数是一些经验的特性。