整数划分问题（Java递归）

整数划分问题（Java递归）

文章目录

• 整数划分问题（Java递归）
• • 0、 问题描述
  • 1、递归式
  • 2、代码
  • 3、参考

---

---

0、 问题描述

整数划分问题

将正整数n表示成一系列正整数之和：n=n₁+n₂+…+n_k，其中n₁≥n₂≥…≥n_k≥1，k≥1。正整数n的这种表示称为正整数n的划分。求正整数n的不同划分个数。

样例

例如正整数6有如下11种不同的划分：

6；
5+1； 
4+2，  4+1+1；
3+3，  3+2+1，3+1+1+1；
2+2+2，2+2+1+1，2+1+1+1+1；
1+1+1+1+1+1

1、递归式

在本例中，如果设p(n)为正整数n的划分数，则难以找到递归关系，因此考虑增加一个自变量：将最大加数n1不大于m的划分个数记作q(n,m)。可以建立q(n,m)的如下递归关系。

q(n,1)=1, n>=1

当最大加数n₁不大于1时，任何正整数n只有一种划分形式，
即n=1+1+1+…+1;

q(n,m)=q(n,n), m>=n

最大加数n₁实际上不能大于n。因此，q(1,m)=1。

q(n,n)=1+q(n,n-1)

正整数n的划分由n₁=n的划分和n₁≤n-1的划分组成。

q(n,m)=q(n,m-1)+q(n-m,m),n>m>1

正整数n的最大加数n₁不大于m的划分由n₁=m的划分和
n₁≤m-1 的划分组成。

递归关系如下：

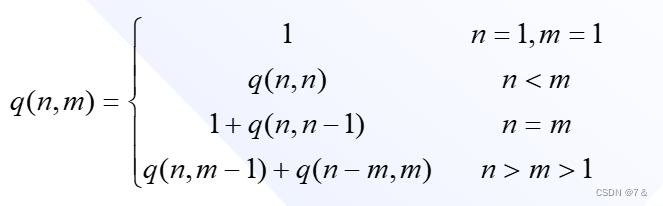
正整数n的划分数p(n)=q(n,n)。

递归图

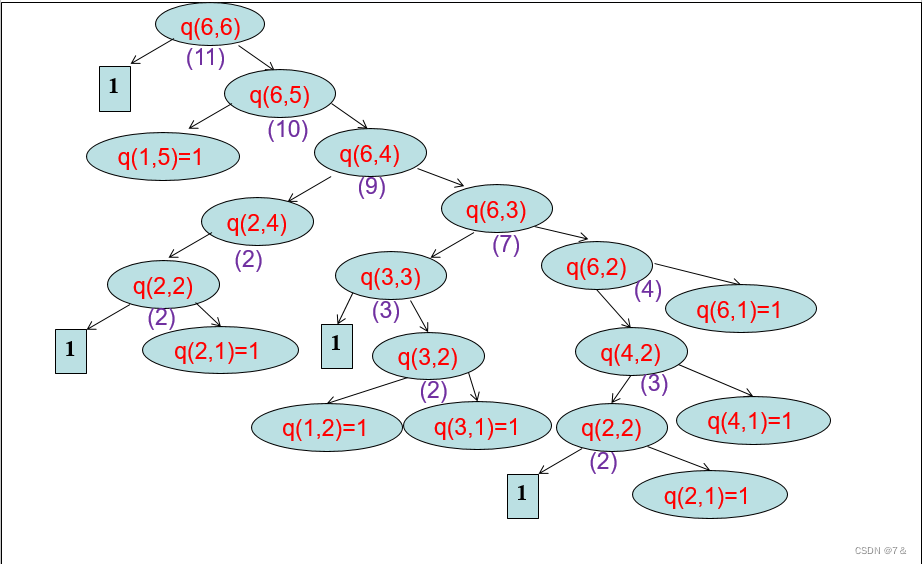
2、代码

对于一个给定的n(n>=1),计算最大加数不超过m的方案数量

public class Solution {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int[] arr = new int[2];
        for (int i = 0; i < arr.length; i++) {
            arr[i] = scanner.nextInt();
        }
        int x = arr[0];
        int y = arr[1];
        if (x < 1 || y < 1) {
            System.out.println("你输入的参数中有非正整数，请返回后重新输入!");
            return;
        }
        System.out.println("对于你输入的参数，求得的整数划分问题的解的个数为:" + helper(x, y));
    }

    public static int helper(int a, int b) {
        if (a == 1 || b == 1)
            return 1;
        if (a < b)
            return helper(a, a);
        if (a == b)
            return helper(a, b - 1) + 1;
        return helper(a, b - 1) + helper(a - b, b);
    }
}

3、参考

• 算法设计与分析（第4版）

结束！