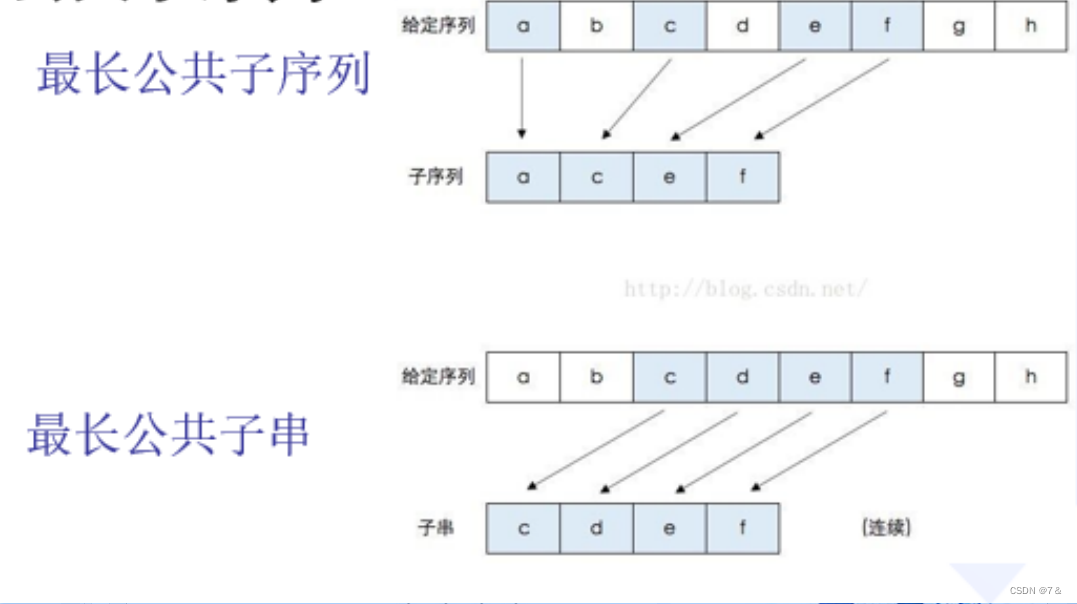
最长公共子序列（LCS）

最长公共子序列（LCS）

文章目录

• 最长公共子序列（LCS）
• • 0、写在前面
  • 1、问题描述
  • 2、最长公共子序列的结构
  • 3、子问题的递归结构
  • 4、计算最优值
  • 5、算法的改进
  • 6、参考

---

---

0、写在前面

本文文字大都来源于下方的参考资料

若给定序列X={x₁,x₂,…,x_m}，则另一序列Z={z₁,z₂,…,zk}，是X的子序列是指存在一个严格递增下标序列{i₁,i₂,…,ik}使得对于所有j=₁,₂,…,k有：z_j=x_i,j。例如，序列Z={B，C，D，B}是序列X={A，B，C，B，D，A，B}的子序列，相应的递增下标序列为{2，3，5，7}。

给定2个序列X和Y，当另一序列Z既是X的子序列又是Y的子序列时，称Z是序列X和Y的公共子序列。

给定2个序列X={x₁,x₂,…,x_m}和Y={y₁,y₂,…,y_n}，找出X和Y的最长公共子序列。

1、问题描述

给定序列 X=<x₁, x₂, … , x_m>, Y=<y₁, y₂, … , yn>，求 X 和 Y 的最长公共子序列

• 实例:

X: A B C B D A B
Y: B D C A B A
一个最长公共子序列: B C B A

蛮力算法：检查 X 的每个子序列在Y 中出现每个子序列 O(n) 时间，X 有 2^_m 个 子序列，最坏情况下时间复杂度：O(n·2^_m)

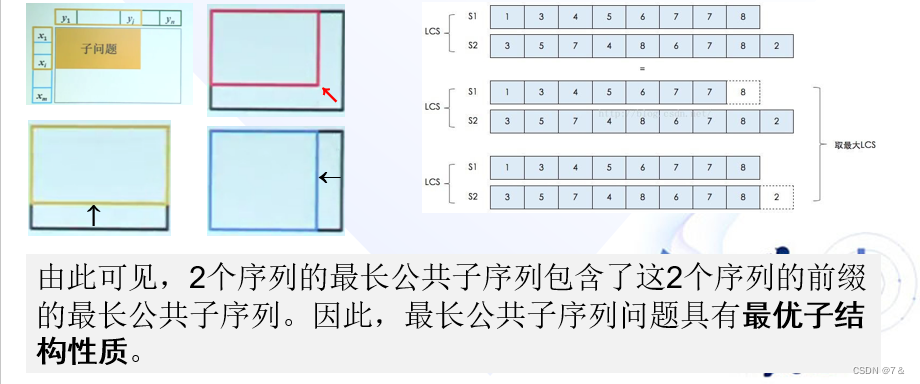
2、最长公共子序列的结构

设序列X={x₁,x₂,…,x_m}和Y={y₁,y₂,…,yn}的最长公共子序列为Z={z₁,z₂,…,zk} ，则

• 若x_m=yn，则zk=x_m=yn，且z_k-1是x_m-1和y_n-1的最长公共子序列。

• 若x_m≠y_n且z_k≠x_m，则Z是x_m-1和Y的最长公共子序列。

• 若x_m≠y_n且z_k≠yn，则Z是X和y_n-1的最长公共子序列。

3、子问题的递归结构

由最长公共子序列问题的最优子结构性质建立子问题最优值的递归关系。用c[i][j]记录序列和的最长公共子序列的长度。其中， X_i={x₁,x₂,…,x_i}；Y_j={y₁,y₂,…,y_j}。当i=0或j=0时，空序列是X_i和Y_j的最长公共子序列。故此时C[i][j]=0。其它情况下，由最优子结构性质可建立递归关系如下：

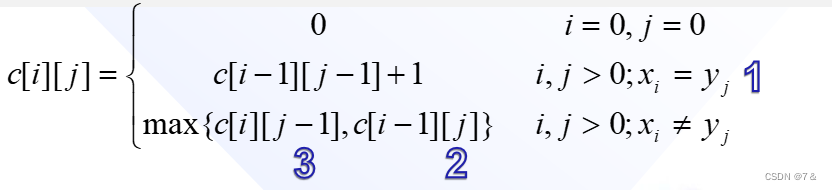
标记函数：B[i, j], 其值为字符↖(1)、⬅ (3)、⬆(2)分别表示C[i,j]取得最大值时的三种情况

4、计算最优值

由于在所考虑的子问题空间中，总共有θ(mn)个不同的子问题，因此，用动态规划算法自底向上地计算最优值能提高算法的效率。

• 计算最长公共子序列的长度

Algorithm lcsLength(x,y,b)
1:m<--x.length;
2:n<--y.length;
3:c[i][0]=0; c[0][i]=0;
4:for (int  i= 1; i <= m; i++)
5:    for (int j = 1; j <= n; j++) 
6:       if (x[i]==y[j]) 
7:           c[i][j]=c[i-1][j-1]+1;
8:           b[i][j]=1; ↖
9:        else if (c[i-1][j]>=c[i][j-1]) 
10:          c[i][j]=c[i-1][j];
11:          b[i][j]=2; ⬆
12:      else 
13:           c[i][j]=c[i][j-1];
14:           b[i][j]=3; ⬇

• 构造最长公共子序列

Algorithm lcs(int i,int j,char [] x,int [][] b) {
    if (i ==0 || j==0) return;
    if (b[i][j]== 1 ↖ ){
      lcs(i-1,j-1,x,b);
      System.out.print(x[i]);
      }
    else if (b[i][j]== 2  ) lcs(i-1,j,x,b);
      else  lcs(i,j-1,x,b);
 }

示例

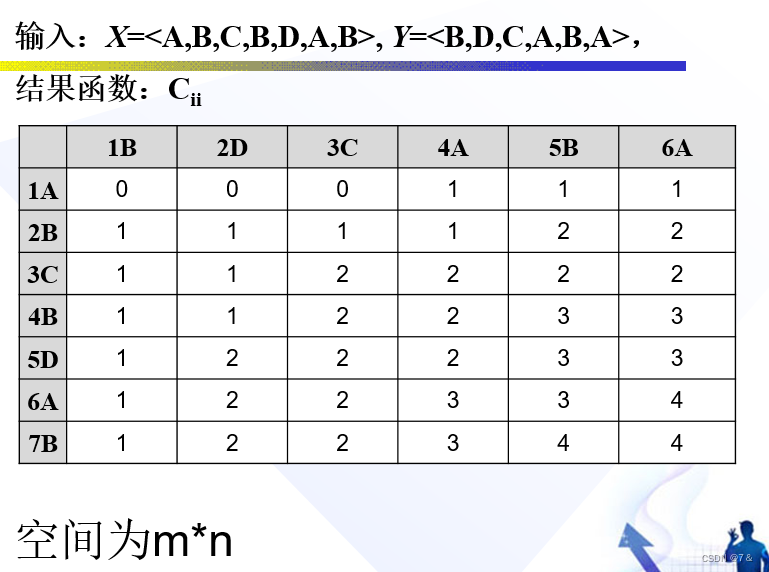
• 输入：

X=<A,B,C,B,D,A,B>, Y=<B,D,C,A,B,A>，

• 结果函数：C_ij

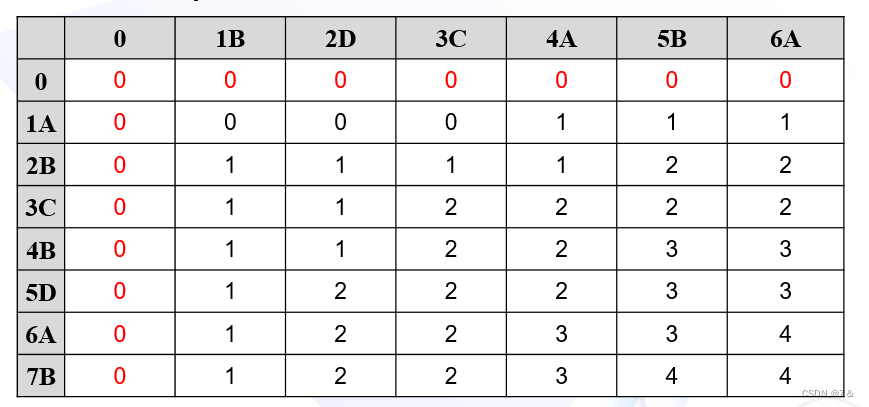
• 解：长度为4

实例

5、算法的改进

• 在算法lcsLength和lcs中，可进一步将数组b省去。事实上，数组元素c[i][j]的值仅由c[i-1][j-1]，c[i-1][j]和c[i][j-1]这3个数组元素的值所确定。对于给定的数组元素c[i][j]，可以不借助于数组b而仅借助于c本身在时间内确定c[i][j]的值是由c[i-1][j-1]，c[i-1][j]和c[i][j-1]中哪一个值所确定的。

• 如果只需要计算最长公共子序列的长度，则算法的空间需求可大大减少。事实上，在计算c[i][j]时，只用到数组c的第i行和第i-1行。因此，用2行的数组空间就可以计算出最长公共子序列的长度。

• 进一步的分析还可将空间需求减至O(min(m,n))。

6、参考

• 算法设计与分析（第4版）

结束！