1.本周学习总结
1.思维导图

2.谈谈你对图结构的认识及学习体会。
图结构相比树更好理解一些。在数据结构的学习当中,我们需要清楚地知道路径的走向。少用到了递归对代码也更容易吸收了解。
在图的学习当中,需要熟练掌握几个算法。emmm因为没上课所以体会会少一些。
- Dljkstra算法
- 本质上是贪心算法,下一条路径都是由当前更短的路径派生出来的更长的路径。不存在回溯的过程。 它每一步都是以当前最优选择为前提的。
- Floyd算法
- Floyd算法实际上是一个动态规划算法,经过三层遍历,是可回溯的。
tips:能用贪心算法解的问题肯定可以由动态规划解。但是可以用动态规划来解的问题,不一定能用贪心算法来解
2.PTA实验作业
2.1.题目1:7-1 图着色问题
图着色问题是一个著名的NP完全问题。给定无向图G=(V,E),问可否用K种颜色为V中的每一个顶点分配一种颜色,使得不会有两个相邻顶点具有同一种颜色?
但本题并不是要你解决这个着色问题,而是对给定的一种颜色分配,请你判断这是否是图着色问题的一个解。
2.1.1设计思路
对于题目样例,形成的邻接表如下:
1->3
2->4->5->1
3->6
4->6
5->6->4
(使用的是头插法,所以形成的邻接表是这个顺序)
然后对于每一种方案,遍历邻接表,如果相邻的情况颜色有一样就直接退出,输出no,如果相邻都不重复就输出yes
void CreateGraph(AdjGraph*& G, int v, int e)
{
G = new AdjGraph;
G->v = v;
G->e = e;
int adjh, adjt;
ArcNode* p;
for i=0 to i<v
初始化邻接表第一个指针为NULL
for i=0 to i<e
cin>>adjh>>adjt;
头插法建立adjh->adjt的邻接表
}
bool IsTrue(AdjGraph*& G, int k)
{
定义color为0;
定义数组visited,初始化为0;
for i=0 to i<G->v
cin>>G->adjlist[i].color;
if visited[顶点颜色] == 0
color++
end if
visited[顶点颜色]++;
if color!=k return false;
定义 p
i = 0;
while i<G->v
p = 第i个顶点的第一个相邻结点
while p!=NULL
if p的颜色和第i个顶点的颜色相同
return false;
end if
p = p->next;
end while
i++;
end while
return true
}
2.1.2代码截图



2.1.3本题PTA提交列表说明。
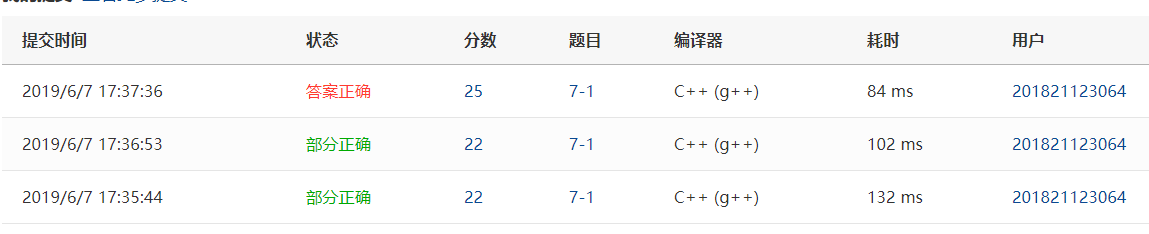
- Q: 最大图出现答案错误
- A: 题目设定有一点 在于 题目的要求是给了k种颜色,一定要用满k种.所以!=的情况下都要return false
2.2.题目2:7-4 公路村村通
现有村落间道路的统计数据表中,列出了有可能建设成标准公路的若干条道路的成本,求使每个村落都有公路连通所需要的最低成本。
2.2.1设计思路
这是一个求最小生成树的问题,使用prim算法解题
特殊的点:本题的要求是任意任意两个村庄都可以有公路连通,所以不可以有非连通图。
定义n,m;
cin >> n >> m;
if m < n-1
cout << "-1";
return 0;
end if
定义 i,j;
for i=0 to i<n
for j=0 to j<n
if i == j
edge[i][j] = 0;
else
edge[i][j] = inf;
end if-else
定义 arch, arcr, info, m_cost;
for i=0 to i<m
cin >> arch >> arcr >> info;
依据arch,arcr,info补全邻接矩阵
for i=0 to i<n
lowcost[i] = edge[0][i];
定义 index为-1,sum为0;
for i=1 to i<n
for j=0 to j<n
找到未修建道路中成本最低的那条路通向的村庄m
if 找到成本最低的路通向的村庄m
sum += m_cost;
lowcost[m] = 0;
else
cout << "-1";
return 0;
end if-else
for j=0 to j<n
if 村庄间未修建道路 && lowcost[j] < edge[m][j]
lowcost[j] = edge[m][j];
end if
cout << sum;
2.2.2代码截图


2.2.3本题PTA提交列表说明。

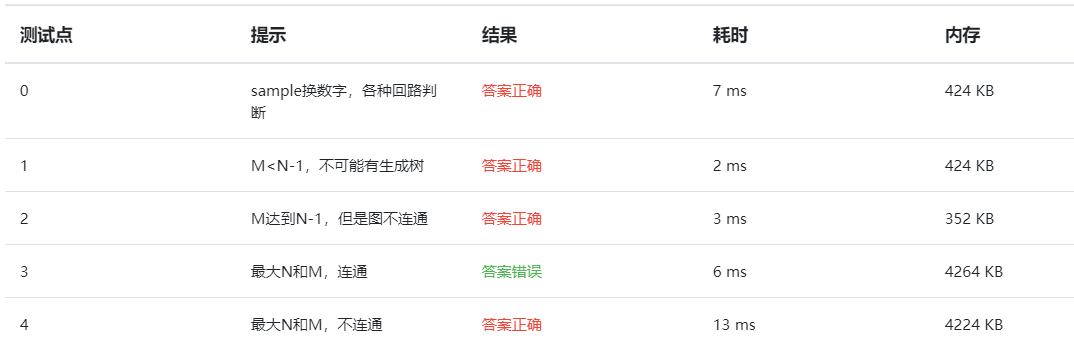
- Q:3样例点答案错误
- A:没有用inf初始化一下邻接矩阵
- Q:1,2,4三个样例点错误
- A:理解错题目意思,以为如果是非连通图,要一个个连通图算过去,求出每个连通图的最小成本之和。但实际上题目意思是,如果是非连通图,直接输出-1
2.3.题目3:7-6 修建道路
N个村庄,从1到N编号,现在请您兴建一些路使得任何两个村庄彼此连通。我们称村庄A和B是连通的,当且仅当在A和B之间存在一条路,或者存在一个存在C,使得A和C之间有一条路,并且C和B是连通的。
已知在一些村庄之间已经有了一些路,您的工作是再兴建一些路,使得所有的村庄都是连通的,并且兴建的路的长度是最小的。
2.1.1设计思路
定义 n,i,j,price,Q,vexi,vexj;
cin >> n;
for i=1 to i<=n
for j=1 to j<=n
cin >> edge[i][j];
cin >> Q;
for i=0 to i<Q
cin >> vexi >> vexj;
依据vexi和vexj将邻接矩阵中已修建道路的点赋值为-1
定义 m_cost,sum=0;
for i=1 to i<=n
将第一个村庄到其他村庄的距离赋值到lowcost数组中
for i=1 to i<n
for j=1 to j<=n
找出未修建道路的村庄中道路距离最短的村庄m
if 找到这个村庄m
sum+=m_cost;
lowcost[m]=0;
end if
for j=1 to j<=n
if 村庄间未修建道路 && lowcost[j] > edge[m][j]
lowcost[j] = edge[m][j];
end if
cout << sum;
2.3.2代码截图


2.3.3本题PTA提交列表说明。

- 这道题和7-4题型主干类似 因此没有碰到其他问题。
3、上机考试错题及处理办法
emmmmm请假没在学校上课所以没有参加考试以下多贴一题编程题的代码(我登陆看考试题集了来着,看不到题目
3.1.题目
六度空间”理论又称作“六度分隔(Six Degrees of Separation)”理论。这个理论可以通俗地阐述为:“你和任何一个陌生人之间所间隔的人不会超过六个,也就是说,最多通过五个人你就能够认识任何一个陌生人。”
“六度空间”理论虽然得到广泛的认同,并且正在得到越来越多的应用。但是数十年来,试图验证这个理论始终是许多社会学家努力追求的目标。然而由于历史的原因,这样的研究具有太大的局限性和困难。随着当代人的联络主要依赖于电话、短信、微信以及因特网上即时通信等工具,能够体现社交网络关系的一手数据已经逐渐使得“六度空间”理论的验证成为可能。
假如给你一个社交网络图,请你对每个节点计算符合“六度空间”理论的结点占结点总数的百分比。
3.2 代码
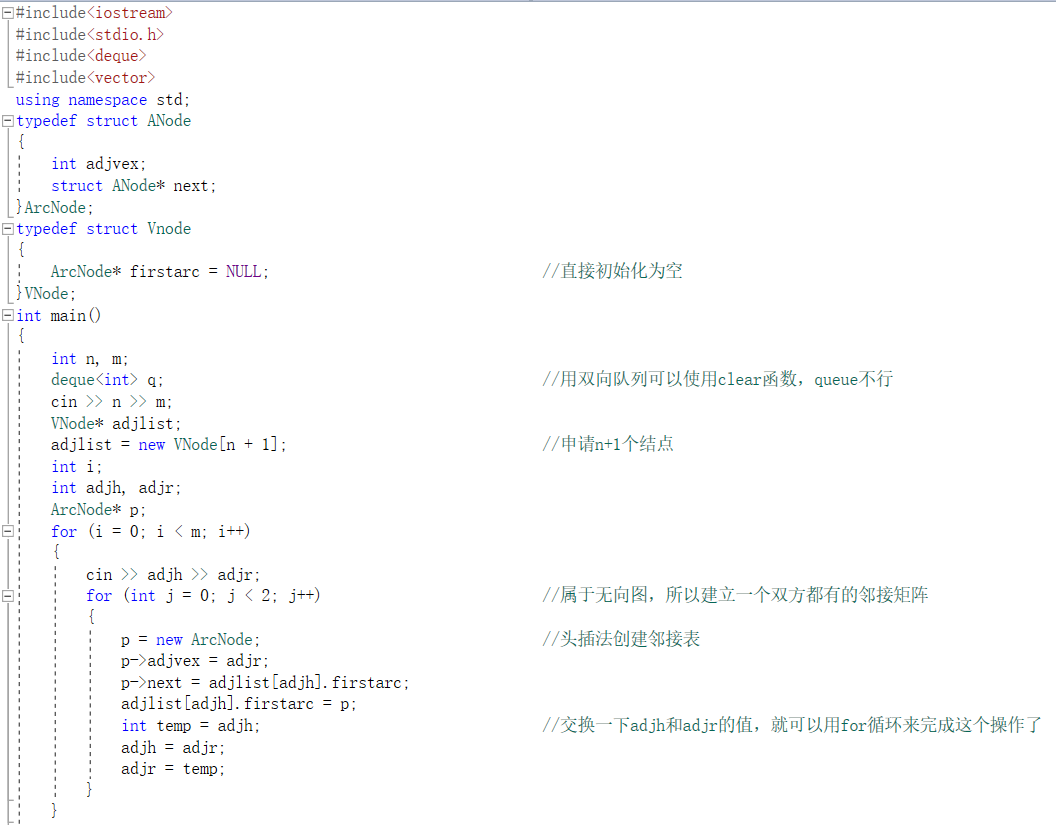


- 中间比较关键的思路
- 需要六次遍历,第一次遍历找到第一个结点相连的其他结点,然后将其他结点依次入队。
第二次遍历则是依次访问其他的结点的相邻结点,然后将这些结点也入队。
重复六次。
比如一个这样的邻接表:
1->2->3
2->4->5
3->5->6
...
第一次:将2,3入队
第二次:先遍历2的相连结点:4,5入队,然后遍历3的:5,6。其中5已经被访问过,所以不入队,只有6入队
...执行六次或者直到邻接表空
- 需要六次遍历,第一次遍历找到第一个结点相连的其他结点,然后将其他结点依次入队。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号