DS博客作业05--树

1.本周学习总结

1.思维导图

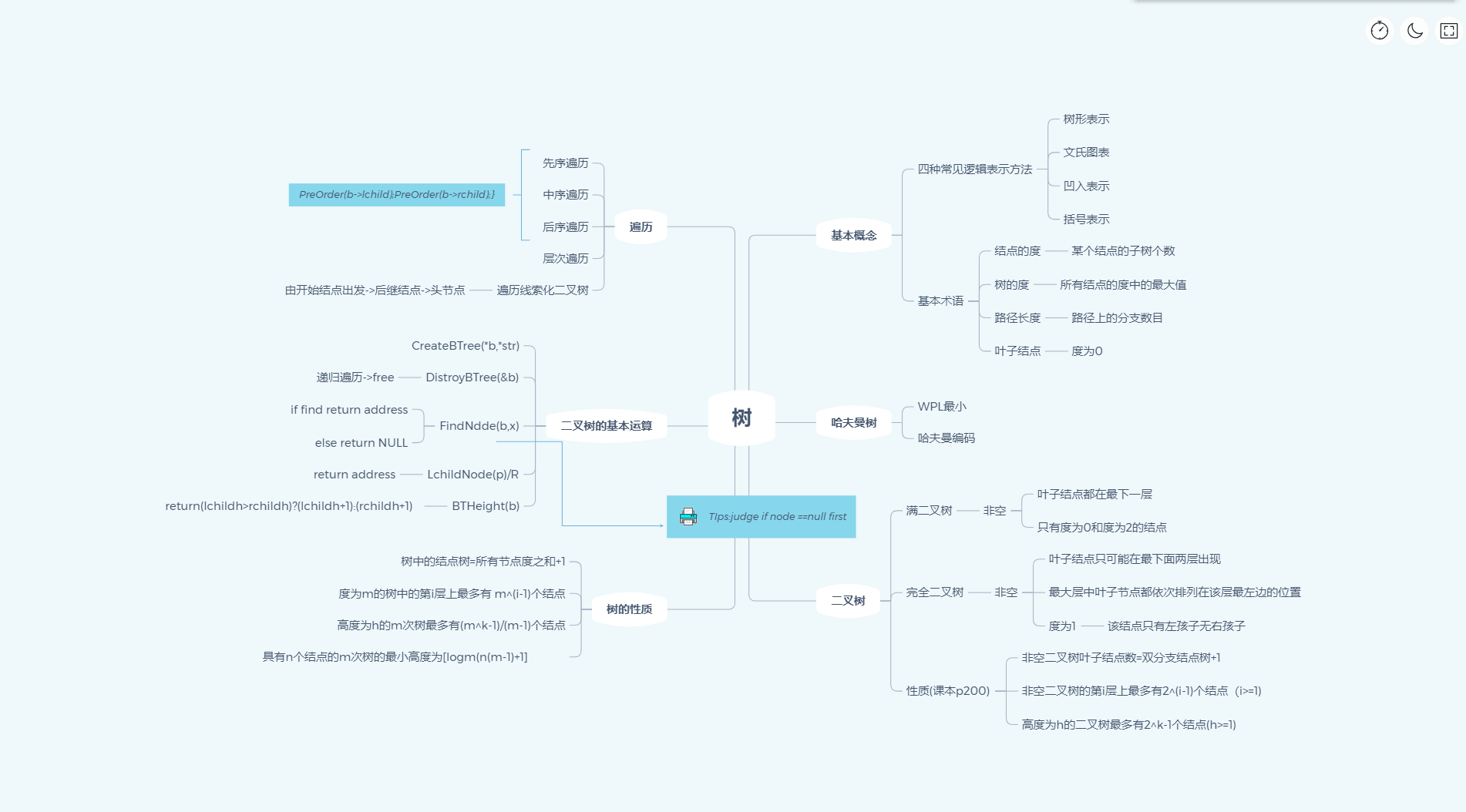
2.谈谈你对树结构的认识及学习体会

• 树结构主要是多分支结构，在建树的过程中更经常用到递归的写法，而在初步的时候学习还是比较抽象的。如果采用非递归的方式进行建树，就有些繁琐。(研究表明，到现在为止离开课本也不能写出个正经非递归代码）1对多的模式使数据的储存模式更加多元化，pta题目中对于我们常用的二叉树进行了一定的训练。另一方面大作业当中再让我们对哈夫曼树深入了解。
• emmmm其实没有很深的学习，最大的体会大概就是心慌慌。因为这两周没有上课还有杂七杂八的原因，所以这块还是很薄弱。看了同学的博客有讲到老师上课讲到的一些写法，正在自己补上。

---

2.PTA实验作业

---

2.1.题目1：表达式树

输入一行中缀表达式，转换一颗二叉表达式树，并求解.
表达式只包含+，-，x，/，（，）运算符，操作数只有一位，且为整数(有兴趣同学可以考虑负数小数，两位数做法)。按照先括号，再乘除，后加减的规则构造二叉树。
如图所示是"1+(2+3)*2-4/5"代数表达式对应二叉树，用对应的二叉树计算表达式的值。 转换二叉树如下：

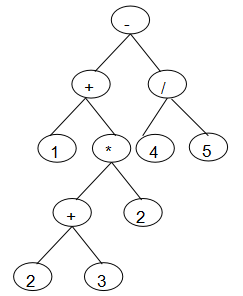
2.1.1设计思路（伪代码）

void InitExpTree(BTree& T, string str)
{
	定义符号栈，数字栈;
	定义 len=str.size();							
	for i = 0 to len
		ch = str.at(i);
	if ch是符号
		判断符号与栈顶符号优先级;
		if < T入栈,op栈顶出栈;
		if > ch入栈;
		if = 栈顶出栈;
	end if;
	if ch是数字
		入栈;
	end if;
	end for;
	逐个出栈;
}
double EvaluateExTree(BTree T)
{
	定义 left,right;
	if T为叶子结点
		return T;
	left = EvaluateExTree(T->lchild);
	right = EvaluateExTree(T->rchild);
	switch (ch)
		answer = left ch right;
	return answer;//得到最终计算结果
}

2.1.2代码截图

2.1.3本题PTA提交列表说明

• Q：除数为0时，输出错误。
• A：在判断除数为0的情况下，直接输出，没有结束程序。此时程序还是在递归的过程当中，没有中止。在这里加上“exit （0）"语句直接退出即可。
• Q：出现各种错误。
• A：对于new的位置处理。如果位置放置错误，将会出现各种错误。

---

2.2.题目2：二叉树层次遍历

层次遍历树中所有节点。 输入一行字符串表示二叉树的顺序存储结构，比如字符串“#ABCD#EF#G##H##I”,#代表空节点。第一个#不使用。
代表二叉树如图所示：

2.2.1设计思路（伪代码）

BTree CreateBTree(string str,int i)
{
   BTree bt;
   bt=new TNode;
   if i超出了字符串长度范围||i=0 return NULL;
   end if;
   if str[i]==# 
	   return NULL;
   end if;
   bt->data =str[i];
   递归建立左子树和右子树; 
   return bt;
}
void LevelOrder(BTree T)
{
	定义队列 q;
	BTree p=T;
	if 树为空
		cout<<"NULL";
		return ;
	while p!=null||队列q!=空		//当p存在或者队列q不为空 
		if p!=null					//注意空格控制
			cout<< p;	
			左右孩子入队;
		end if;
	end while;
	}
}

2.2.2代码截图

2.2.3本题PTA提交列表说明

• Q：当二叉树为空时，答案错误。
• A：在输出内容上出现错误，重新看题目才发现问题所在。

---

2.3.题目3：输出二叉树每层节点

层次遍历树中所有节点。输出每层树节点。
树结构按照树的先序遍历递归建树，比如先序遍历字符串“ABD#G###CEH###F#I##”#代表空节点。对应树结构如下图,

2.3.1设计思路（伪代码）

Tree TreeBuild(string str, int i)
{
	Tree T = new TREE;
	if i超出str范围 || str[i]== '#'
		return NULL;
	end if;
	T->data = str.at(i);
	递归建立左右子树; 
	return T;
}
void LevelOrder(Tree T)
{
	if 树空
		cout NULL;
		return;
	end if
	定义 queue q;
	定义 p 并置空;
	q.push(T);
	for h = 1 to q空 
		输出h和符号':';  
		while q!=空 && 未全部输出		
			PopQueue(p,q);
			if p!=NULL
				cout <<p;
				if child != null 入队；
				else 记录于nullnum; 
			end if；
		end while;
	end for;
		求出下一层的最多可容纳结点数量levelnum; 
		effecient_num = levelnum - nullnum;						//用这一层的最大结点个数-空结点的个数，得到这一层要输出多少结点 
}

2.3.2代码截图

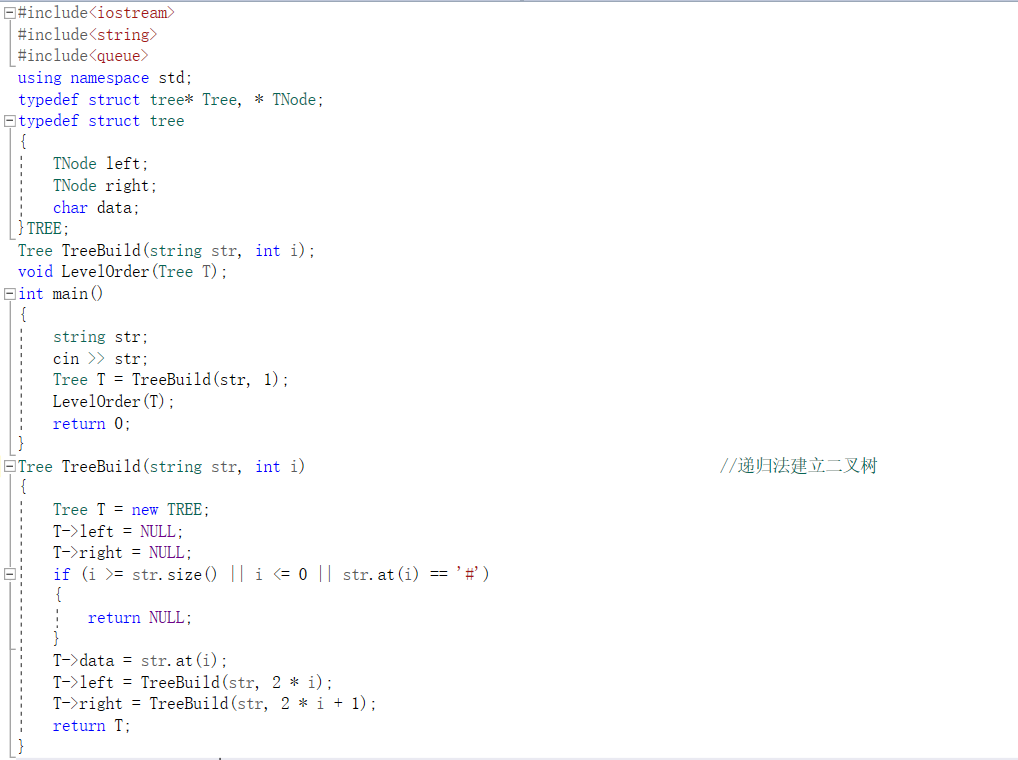
2.3.3本题PTA提交列表说明

• Q：在建树上与题目要求有所出入。原代码如下

Tree TreeBuild(string str, int i)
{                 
	Tree T = new TREE;
	T->left = NULL;
	T->right = NULL;
	if (i >= str.size() || i < 0 || str.at(i) == '#')
	{
		return NULL;
	}
	T->data = str.at(i);
	T->left = TreeBuild(str, 2 * i);
	T->right = TreeBuild(str, 2 * i + 1);
	return T;
}

• A：模仿题目给出的先序遍历的样例作出修改，使得非空情况能够正常运行。
• Q：第一层输出后出现各种错误。
• A：每遍历一层，需要将nullnum重新初始化为0

---

3.阅读代码

3.1 题目

给定一个二叉树，判断其是否是一个有效的二叉搜索树。

• 假设一个二叉搜索树具有如下特征：
  • 节点的左子树只包含小于当前节点的数。
  • 节点的右子树只包含大于当前节点的数。
  • 所有左子树和右子树自身必须也是二叉搜索树。
    

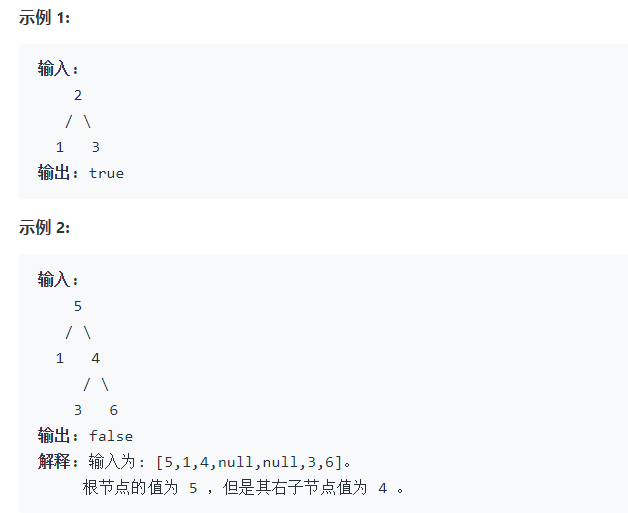
3.2 解题思路

利用Morris算法进行中序遍历； 遍历的同时将当前输出的值与之前输出的值进行比较，如果当前值小于或等于之前的输出值，则直接返回false

• 参考1：https://www.cnblogs.com/AnnieKim/archive/2013/06/15/MorrisTraversal.html

• 参考2：http://blog.csdn.net/mxw976235955/article/details/39829973

• Morris算法

  • 其时间复杂度仍然是O(n)，但是空间复杂度却只有O(1)。O(1)空间复杂度，即只能使用常数空间
  • 二叉树的形状不会被破坏（中间过程允许改变其形状）。

3.3 代码截图

3.4 学习体会

• 在整个数据结构的过程当中，会更加偏向于算法的学习。而树的学习当中更加注重递归的用法。
• 而Morris算法，则可以很大程度上使空间复杂度降低。要使用O(1)空间进行遍历，最大的难点在于，遍历到子节点的时候怎样重新返回到父节点。Morris方法用到了线索二叉树的概念。在Morris方法中不需要为每个节点额外分配指针指向其前驱和后继节点，只需要利用叶子节点中的左右空指针指向某种顺序遍历下的前驱节点或后继节点就可以了。
• 学习一种比较优化的算法的同时，巩固线索二叉树。[qaq虽然还不太会用啦]