1.自编码器
2.contractive auto-encoder CAE(收缩自编码器)
1.自编码器
内容来源:
https://www.cnblogs.com/klausage/p/12582421.html
https://www.baidu.com/link?url=uWT564giDq14x-JaKmDhQD4JD37sPrVRgi7vNVPA3FsP_S_ffybOAqPDxydGudLbd_e_BAZSr91VbR6-Oz5hx_&ck=5985.7.85.481.274.467.350.561&shh=www.baidu.com&sht=98010089_dg&wd=&eqid=9ed1b3ad000912fe000000055f2b523f
https://www.baidu.com/link?url=riADYY-v58t-18h4AY7XoUcNLPXGcPNoLMt2suLFpKk7bWTEHfjS74cMW7p2PgmWnRc0MR2kmJbgRS2h88VBIdgNdOQUl7UR0KYJxcH533K&ck=6198.9.137.360.298.467.350.181&shh=www.baidu.com&sht=98010089_dg&wd=&eqid=9ed1b3ad000912fe000000055f2b523f
自编码器(autoencoder, AE)是一类在半监督学习和非监督学习中使用的人工神经网络(Artificial Neural Networks, ANNs),其功能是通过将输入信息作为学习目标,对输入信息进行表征学习(representation learning) [1-2] 。
自编码器包含编码器(encoder)和解码器(decoder)两部分 [2] 。按学习范式,自编码器可以被分为收缩自编码器(undercomplete autoencoder)、正则自编码器(regularized autoencoder)和变分自编码器(Variational AutoEncoder, VAE),其中前两者是判别模型、后者是生成模型 [2] 。按构筑类型,自编码器可以是前馈结构或递归结构的神经网络。
自编码器具有一般意义上表征学习算法的功能,被应用于降维(dimensionality reduction)和异常值检测(anomaly detection) [2] 。包含卷积层构筑的自编码器可被应用于计算机视觉问题,包括图像降噪(image denoising) [3] 、神经风格迁移(neural style transfer)等 [4] 。
AE历史:
自编码器在其研究早期是为解决表征学习中的“编码器问题(encoder problem)”,即基于神经网络的降维问题而提出的联结主义模型的学习算法。1985年,David H. Ackley、Geoffrey E. Hinton和Terrence J. Sejnowski在玻尔兹曼机上对自编码器算法进行了首次尝试,并通过模型权重对其表征学习能力进行了讨论 [6] 。在1986年反向传播算法(Back-Propagation, BP)被正式提出后,自编码器算法作为BP的实现之一,即“自监督的反向传播(Self-supervised BP)”得到了研究 [7] ,并在1987年被Jeffrey L. Elman和David Zipser用于语音数据的表征学习试验 [8] 。自编码器作为一类神经网络结构(包含编码器和解码器两部分)的正式提出,来自1987年Yann LeCun发表的研究 [5] 。LeCun (1987)使用多层感知器(Multi-Layer Perceptron, MLP)构建了包含编码器和解码器的神经网络,并将其用于数据降噪。此外,在同一时期,Bourlard and Kamp (1988)使用MLP自编码器对数据降维进行的研究也得到了关注 [9] 。1994年,Hinton和Richard S. Zemel通过提出“最小描述长度原理(Minimum Description Length principle, MDL)”构建了第一个基于自编码器的生成模型 [10] 。
1、什么是生成模型?
概率统计层面:能够在给丁某一些隐含参数的条件下,随机生成观测数据的这样一种模型,称之为“生成模型”。它给观测值和比周数据系列制定一个连和概率分布
机器学习层面:直接对数据进行建模,比如根据某个变量的概率密度函数进行数据采样。在贝叶斯算法中,直接对连和概率分布P(x,y)进行建模,然后利用贝叶斯公式进行求解P(y|x)。
2、生成模型的两大类型
第一类:完全表示出数据确切的分布函数
第二类:没有办法完全表示出确切的分布函数,但是,能够做到的是新的数据的生成,而具体的分布函数是模糊的。
在机器学习中,不管是自编码器AE、变分自编码器VAE、还是生成对抗网路GAN,都是属于第二类。生成新数据,也是大部分生成模型的核心目标。
自编码器是一种无监督学习技术,利用神经网络进行表征学习。也就是说,我们设计一个在网络中施加“瓶颈”,迫使原始输入压缩知识表示的神经网络架构。如果输入特征彼此独立,则该压缩和随后的重构将是非常困难的任务。但是,如果数据中存在某种结构(即输入特征之间存在相关性),则可以学习这种结构,并在强制输入通过网络的瓶颈时使用。
自编码器可以认为是一种数据压缩算法,或特征提取算法。
自编码器的两个重要特征
(1)压缩编码的数据维度一定要比元时输入数据更少。也就是所谓的要具有一定的“瓶颈限制”,如果压缩编码的数据维度更多,那就到不到数据降维的目的了,那编码还有什么意义呢?
(2)不管是编码器,还是解码器,本质上都是神经网络层,神经网络层一定要具有一定的“容量(capacity)”。什么是容量,就是一定要不止一个神经网络层才行,为什么?因为我们知道神经网络层数意味着对数据的隐含特征进行提取(虽然我不知道到底是怎么提取的,但是我知道一定是有隐含关联性的),如果向上面的只有一个中间的压缩编码数据层,此时我们的数据输入层与编码输出层是直接相连接的,如果我在神经元节点上不使用非线性激活函数,我们发现,这会得到和PCA类似的降维效果。所以,最好是多添加剂个网络层,来储存输入数据之间的那些隐含关系,存储它们的潜在特征和关联。
总结起来:自编码器需要“瓶颈+容量”
自编码器指的是试图让输出和输入一样的神经网络。他们通过将输入压缩成一个隐藏空间表示来进行工作,然后通过这种表示重构输出。
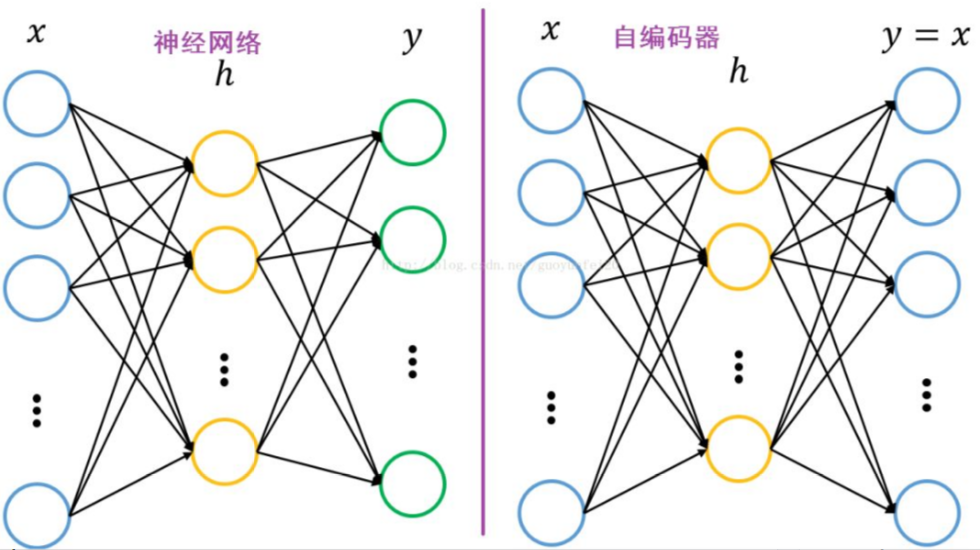
如果autoencoders的唯一目的是将输入复制到输出中,那么它们将毫无用处。 实际上,我们希望通过训练autoencoder将输入复制到输出中,隐藏表示h将具有有用的属性。
这可以通过在复制任务上添加一些限制条件进行实现。从自编码器获得有用特征的一种方法是将h限制为小于x的维度,在这种情况下,自编码器是不完整的。通过训练不完整的表示,我们强制自编码器学习训练数据的最显著特征。如果自编码器的容量过大,自编码器可以出色地完成赋值任务而没有从数据的分布抽取到任何有用的信息。如果隐藏表示的维度与输入相同,或者隐藏表示维度大于输入维度的情况下,也会发生这种情况。在这些情况下,即使线性编码器和线性解码器也可以将输入复制到输出,而无需了解有关数据分配的任何有用信息。理想情况下,自编码器可以成功地训练任何体系结构,根据要分配的复杂度来选择编码器和解码器的代码维数和容量。
当前,数据去噪和数据可视化中的降维被认为是自编码器的两个主要的实际应用。通过适当的维度和稀疏性约束,自编码器可以学习比PCA或其他基本技术更有趣的数据投影。
自编码器通过数据样本自动学习。这意味着很容易训练特定的算法实例,该算法在特定类型的输入中表现良好,并且不需要任何新工程,只需要适当的训练数据。
但是,自编码器在图像压缩方面做得不好。 由于自编码器是在给定的一组数据上进行训练的,因此它将对类似于所用训练集中的数据实现合理的压缩结果,但是作为图像压缩器效果是不好的。 像JPEG这样的压缩技术效果比自编码器效果好很多。
自编码器经过训练,可以在输入通过编码器和解码器后保留尽可能多的信息,但也会接受训练以使新的表示具有各种不错的属性。 不同类型的自编码器旨在实现不同类型的属性。
- 普通自编码器/多层自编码器(欠完备的自编码器)
普通自编码器是三层网络,即具有一个隐藏层的神经网络。 输入和输出是相同的,我们将学习如何重构输入,例如使用adam优化器和均方误差损失函数。
如果一个隐藏层不够用,我们显然可以将自编码器扩展到更多的隐藏层。
现在我们的实现使用3个隐藏层,而不是一个。 任何隐藏层都可以作为特征表示,但我们将使网络结构对称并使用最中间的隐藏层。
adam优化算法:
https://baijiahao.baidu.com/s?id=1668617930732883837&wfr=spider&for=pc
由于神经网络能够学习非线性关系,因此可以认为这是PCA更有力(非线性)的泛化。而PCA试图发现描述原始数据的低维超平面,自编码器则能够学习非线性流形(流形为连续的非交叉的曲面)
欠完备自编码器没有明确的正则化项,只是根据重构损失来训练我们的模型。因此,确保模型不记忆输入数据的唯一方法就是确保我们已经充分限制了隐藏层中的节点数量。
- 正则化的自编码器
还有其他一些方法可以限制自编码器的重构,而不是简单地强加一个维度比输入小的隐藏层。 正规化自编码器不是通过调整编码器和解码从而限制模型容量,而是使用损失函数,鼓励模型学习除了将输入复制到其输出之外的其他属性。 在实践中,我们通常会发现两种正规化自编码器:稀疏自编码器和去噪自编码器。
稀疏自编码器:稀疏自编码器通常用于学习分类等其他任务的特征。 稀疏自编码器必须响应数据集独特的统计特征,而不仅仅是作为标识函数。 通过这种方式,用稀疏性惩罚来执行复制任务的训练可以产生有用的特征模型。
我们可以限制自编码器重构的另一种方式是对损失函数施加约束。 例如,我们可以在损失函数中添加一个修正术语。 这样做会使我们的自编码器学习数据的稀疏表示
注意在我们的正则项中,我们添加了一个l1激活函数正则器,它将在优化阶段对损失函数应用一个惩罚。 在结果上,与正常普通自编码器相比,该表示现在更稀松。
去噪自编码器:我们可以获得一个自编码器,通过改变损失函数的重构误差项来学习一些有用的东西,而不是对损失函数加以惩罚。 这可以通过给输入图像添加一些噪声并使自编码器学会移除噪声从而来进行训练。 通过这种方式,编码器将提取最重要的特征并学习数据的更鲁棒的表示。
压缩自编码器:人们会期望对于非常相似的输入,学习的编码也会非常相似。我们可以为此训练我们的模型,以便通过要求隐藏层激活的导数相对于输入而言很小。换句话说,对于输入比较小的改动,我们仍然应该保持一个非常类似的编码状态。这与降噪自编码器相似,因为输入的小扰动本质上被认为是噪声,并且我们希望我们的模型对噪声具有很强的鲁棒性。“降噪自编码器使重构函数(解码器)抵抗输入有限小的扰动,而压缩自编码器使特征提取函数(编码器)抵抗输入无限小的扰动。“
因为我们明确地鼓励我们的模型学习一种编码,在这种编码中,类似的输入有类似的编码。我们基本上是迫使模型学习如何将输入的临近区域收缩到较小的输出临近区域。注意重构数据的斜率(即微分)对于输入数据的局部邻域来说基本为零
- 变分自编码器——VAE
当我们对解码器输入一个训练集中从未出现的编码的时候,我们得到的重构的输出可能是一个完全的乱码或者是噪声,也就是说与手写数字数据毫无关系,很显然,这并不是我们所希望的。我们希望的是“生成模型”能够对任意的输入编码产生有相关意义的数据,这就是“变分自编码器VAE”所要做的事情。
自编码器



2.contractive auto-encoder


Jacobi 方法是求对称矩阵的全部特征值以及相应的特征向量的一种方法
矩阵范数
https://www.jianshu.com/p/4ca905ff47cc



近端梯度算法(Proximal Gradient Method)
variational autoencoders 变分自编码器VAE
generative adversarial networks 生成对抗网络GAN
Restricted Boltzmann Machines 受限玻尔兹曼机RBM
auto-encoder
contractive auto-encoder
under-complete auto-encoder 欠完备自编码器
Principal Component Analysis





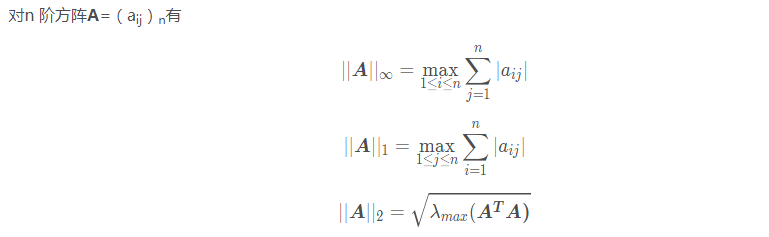

 浙公网安备 33010602011771号
浙公网安备 33010602011771号