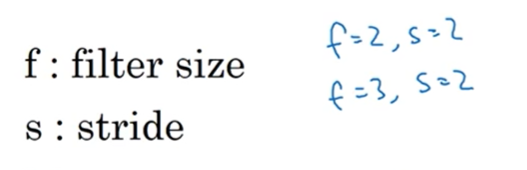- 原理
- 卷积层
- 单通道图
- 俗称灰度图,每个像素点只能有有一个值表示颜色,它的像素值在0到255之间,0是黑色,255是白色,中间值是一些不同等级的灰色。(也有3通道的灰度图,3通道灰度图只有一个通道有值,其他两个通道的值都是零)
- 卷积核(过滤器)(滤波器)(特征提取器)(权重矩阵)
- 卷积核的作用在于特征的抽取,越是大的卷积核尺寸就意味着更大的感受野,当然随之而来的是更多的参数。
- 在达到相同感受野的情况下,卷积核越小,所需要的参数和计算量越小。
- 设计原则
- 卷积核一般形状是奇数的。如3x3,5x5,7x7,这样的原因是保证一定会有个中心点。
- 卷积核的各个元素值一般相加等于1,这样做的原因是保证原图像经过卷积核的作用亮度保持不变(但该原则不是必须)。
- 卷积核的大小确定(filter)
- f通常是奇数
- f是偶数,你只能使用不对称填充,只有f是奇数,same卷积才能使用自然填充
- 奇数过滤器有中心点好确定位置
- 具体来说。卷积核大小必须大于1才有提升感受野的作用,1排除了。而大小为偶数的卷积核即使对称地加padding也不能保证输入feature map尺寸和输出feature map尺寸不变(画个图算一下就可以发现),2排除了。所以一般都用3作为卷积核大小。
- 卷积核里的值
- 卷积核里具体数值(以下用符号W表示)是最终学习所得出的参数,是学习过程计算出来的。
- 目前常用初始化的方法会遵循这样的思路:将其随机初始化为较小的接近0的小数。
- 将3*3过滤器中的九个数设置为九个参数,让神经网络自动去学习,用BP算法反向传播
- 卷积核的作用
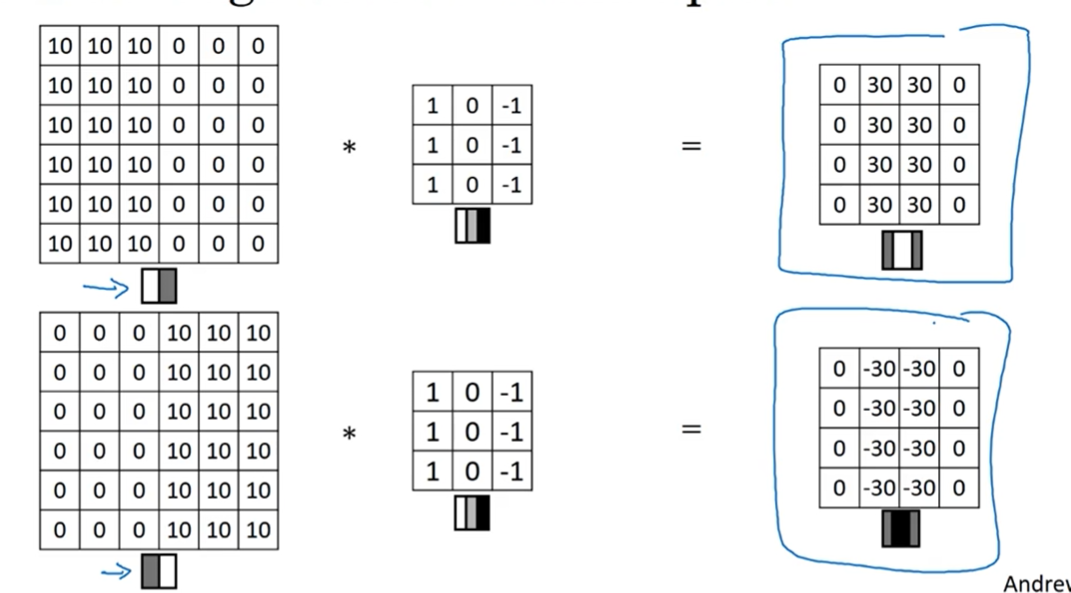
- 特别的垂直边缘检测器
- 边缘检测器
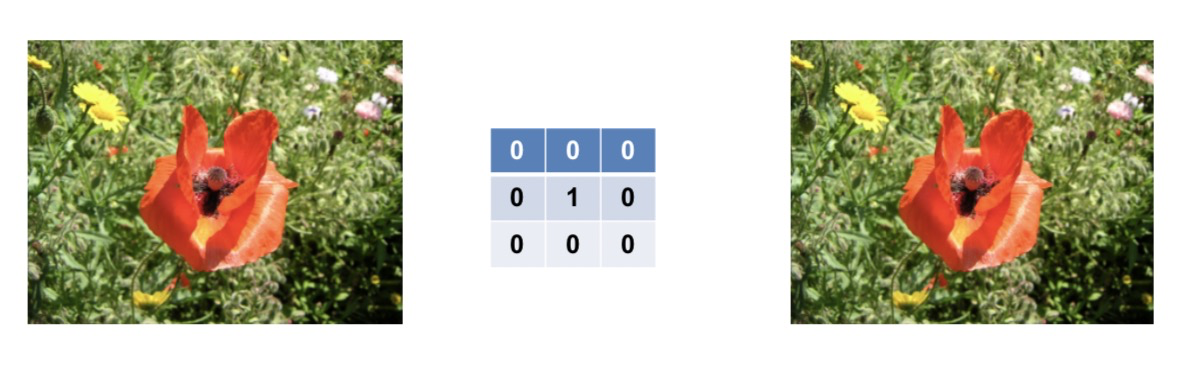
- 与原图像保持不变
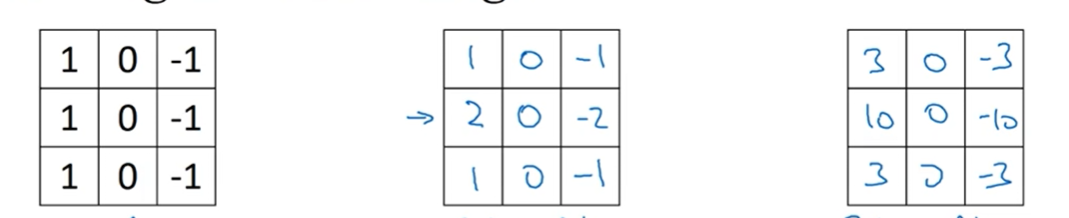
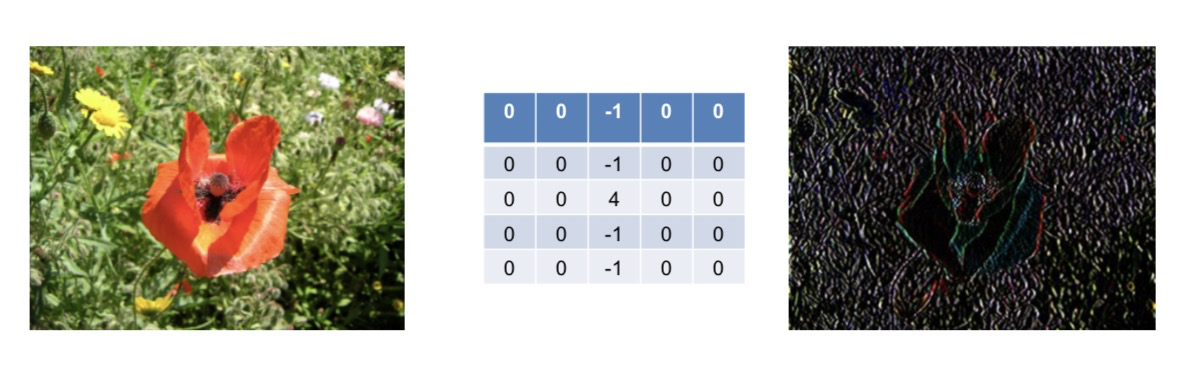
- 刻画原图像的水平边缘
- 原因:
- 假设第一个-1值对应的像素是X0,第二个-1对应的像素是X1,-2对应的像素值是X2,那么因为图像的边缘的像素基本保持一致,所以会有:2X2-X1-X0≈0,那么会将这样的水平线以比较暗的图像展示出来。
- 示例
- 刻画原图像的垂直边缘
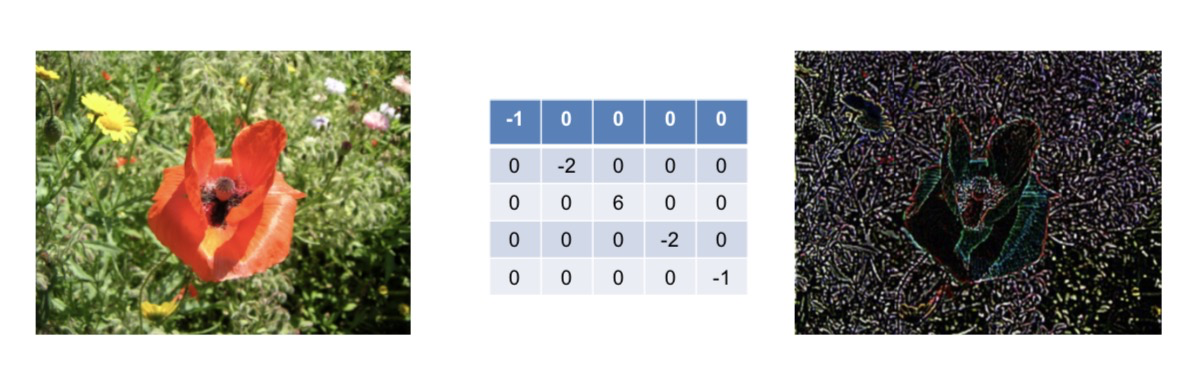
- 刻画原图像45度的边缘
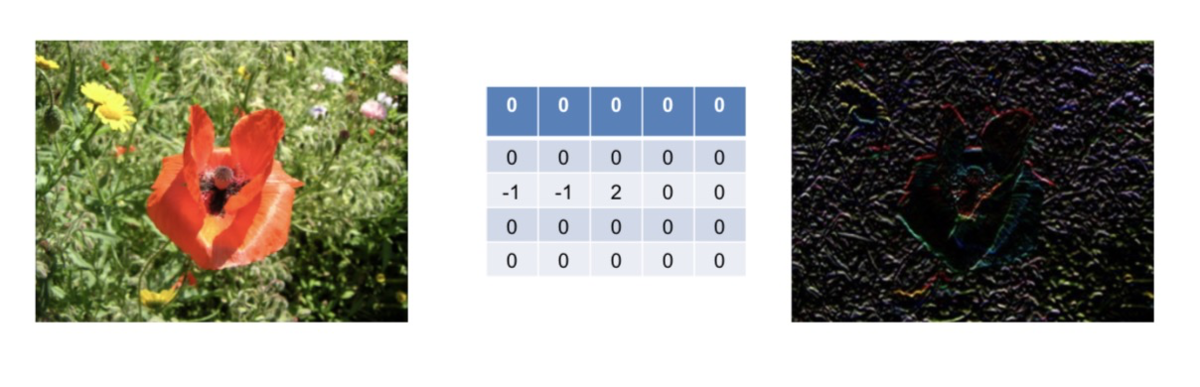
- 锐化效果
- 显示边缘亮
- 浮雕效果
- CNN中卷积核的特点
- CNN 可以看作是 DNN 的一种简化形式,即这里卷积核中的每一个权值就可以看成是 DNN 中的 ,且与 DNN 一样,会多一个参数偏置。
- 一个卷积核在与 Input 不同区域做卷积时,它的参数是固定不变的。放在 DNN 的框架中理解,就是对同一层 Layer 中的神经元而言,它们的 和 是相同的,只是所连接的节点在改变。因此在 CNN 里,这叫做 共享权值偏置。
- 在 CNN 中,卷积核可能是高维的。假如输入是 维的,那么一般 卷积核就会选择为 维,也就是与输入的 Depth 一致。
- 最重要的一点,在 CNN 中,卷积核的权值不需要提前设计,而是跟 DNN 一样利用 GD 来优化,我们只需要初始化。
- 如上面所说,其实卷积核卷积后得到的会是原图的某些特征(如边缘信息),所以在 CNN 中,卷积核卷积得到的 Layer 称作特征图。
- 一般 CNN 中两层之间会含有多个卷积核,目的是学习出 Input 的不同特征,对应得到多个特征图。又由于卷积核中的参数是通过 GD 优化得到而非我们设定的,于是初始化就显得格外重要了。[1]
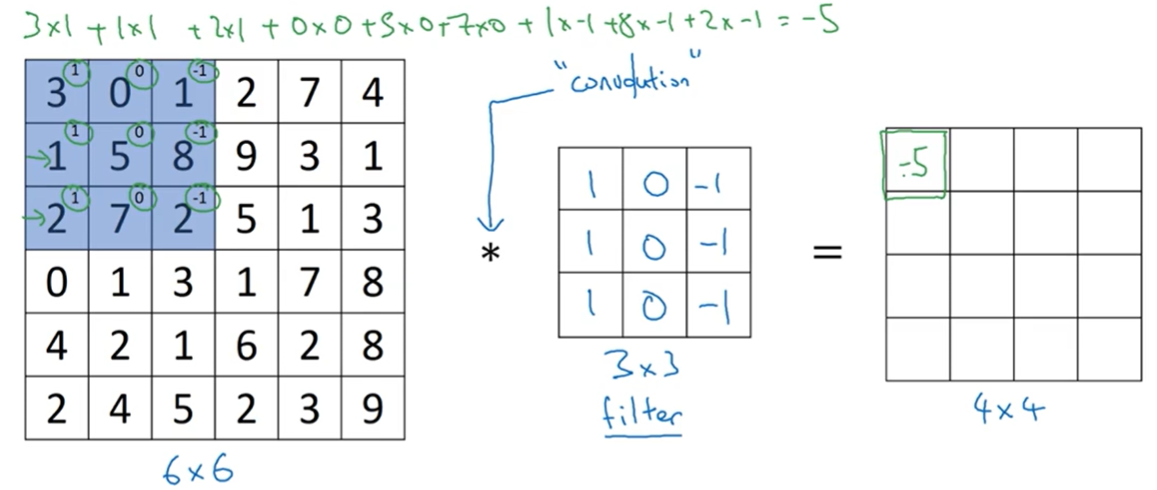
- 卷积计算
- 卷积操作的函数
- tf.nn.conv2d(x, filter=w, strides=[1, stride, stride, 1], padding=padding)
- tf.nn.conv2d(
- input,
- filter,
- strides,
- padding,
- use_cudnn_on_gpu=True,
- data_format='NHWC',
- dilations=[1, 1, 1, 1],
- name=None
- )
- 示例
- 卷积运算的问题
- Padding填充
- 概念
- 在卷积运算之前,进行填充
- Padding=1意为填充一个像素点
- 分类
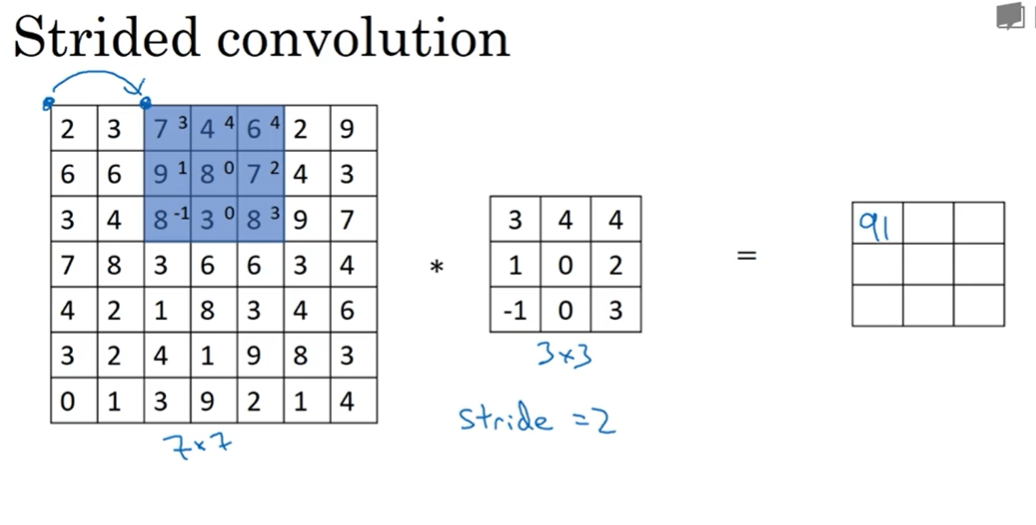
- stride步长
- 回归函数
- 选择取决于类别之间是否互斥
- logic回归:二分类问题,输出层为一个节点
- softmax回归:多分类问题,输出层为K(K>2)个节点
- 池化层
- 池化函数
- pool(input,window_shape,pooling_type,padding,dilation_rate,strides,name,data_format)
- avg_pool(value,ksize,strides,padding,data_format,name)//平均池化
- max_pool(value,ksize,strides,padding,data_format,name)//最大池化
- #ksize 参数提供了过滤器的尺寸,strides 参数提供步长信息
- #padding 提供是否使用全0填充
- padding:VALD 表示不使用全0 填充。 SAME表示使用全0 填充。
- 最大池化和平均池化
- 池化过程中没有需要学习的参数
- 常用过滤器参数
- 全连接层
- 优势
- 参数共享
- 稀疏连接
- 共享权值(卷积核)带来的直接好处是减少网络各层之间的连接,同时又降低了过拟合的风险
- 数据增强
posted on
2020-02-02 20:33
生长的力量
阅读(
619)
评论()
编辑
收藏
举报