题目链接:http://poj.org/problem?id=2585
构图稍微复杂点,根据题目描述得到一个窗口的覆盖关系,根据覆盖关系可以构造一个有向图, 以9个窗口为顶点,如果A号窗口可以覆盖B号窗口,则有一条有向边<A,B>,构造完有向图后,如果是一个正常屏幕,则图为有向无环图(因为不可能存在A覆盖B,B覆盖A),所以该题可以拓扑排序判断环来解决。
例如:题目中给的两个样例,可以构造为
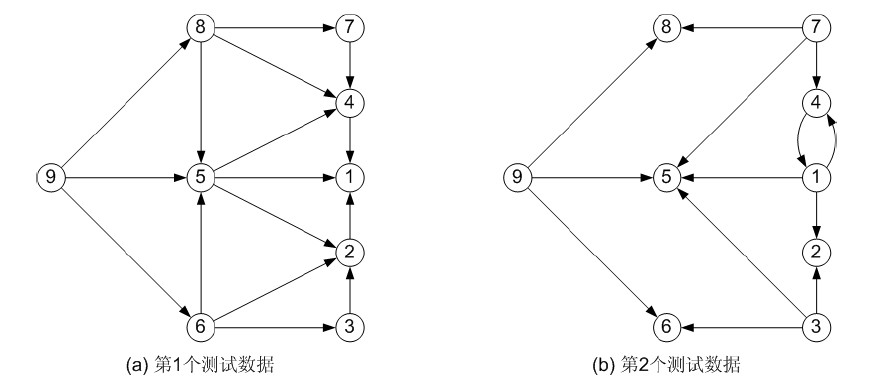
由图可知,第一组样例没有出现环,即屏幕是正常的,第二组样例出现了环,所以屏幕是不正常的。
代码:
1 #include <iostream>
2 #include <cstring>
3 #include <string>
4 #include <cstdio>
5 using namespace std;
6 const int N=5;
7 int map[10][10];//邻接矩阵
8 int screen[N][N];//屏幕最后显示的内容
9 string cover[N][N];//能覆盖(i,j)位置的窗口
10 string s;
11 int vis[10];//标记
12 int id[10];//入度
13 int t;//记录出现的窗口种类数
14
15 void cal()//初始化cover
16 {
17 int k,i,j;
18 for(i=0;i<N;i++)
19 for(j=0;j<N;j++)
20 cover[i][j].erase();
21 for(k=1;k<=9;k++)
22 {
23 i=(k-1)/3;
24 j=(k-1)%3;
25 cover[i][j]+=(char)(k);
26 cover[i][j+1]+=(char)(k);
27 cover[i+1][j]+=(char)(k);
28 cover[i+1][j+1]+=(char)(k);
29 }
30 }
31
32 void build()//构造有向图
33 {
34 int i,j,k;
35 for(i=0;i<N-1;i++)
36 {
37 for(j=0;j<N-1;j++)
38 {
39 for(k=0;k<cover[i][j].length();k++)
40 {
41 if((!map[screen[i][j]][cover[i][j][k]]) && (screen[i][j]!=cover[i][j][k]))
42 {
43 map[screen[i][j]][cover[i][j][k]]=1;
44 id[cover[i][j][k]]++;
45 }
46 }
47 }
48 }
49 }
50
51 int topo()//拓扑排序,判环
52 {
53 int i,j,k;
54 for(i=0;i<t;i++)
55 {
56 k=1;
57 while(!vis[k] || (k<=9&&id[k]>0))
58 k++;
59 if(k>9)
60 return 0;
61 vis[k]=0;
62 for(j=1;j<10;j++)
63 {
64 if(vis[j]&&map[k][j])
65 id[j]--;
66 }
67 }
68 return 1;
69 }
70
71 int main()
72 {
73 int i,j,k;
74 cal();
75 while(cin>>s)
76 {
77 if(s=="ENDOFINPUT")
78 break;
79 memset(id,0,sizeof(id));
80 memset(vis,0,sizeof(vis));
81 memset(map,0,sizeof(map));
82 t=0;
83 for(i=0;i<N-1;i++)
84 {
85 for(j=0;j<N-1;j++)
86 {
87 scanf("%d",&k);
88 if(!vis[k])
89 {
90 t++;
91 vis[k]=1;
92 }
93 screen[i][j]=k;
94 }
95 }
96 build();
97 if(topo())
98 puts("THESE WINDOWS ARE CLEAN");
99 else
100 puts("THESE WINDOWS ARE BROKEN");
101 cin>>s;
102 }
103 return 0;
104 }
2 #include <cstring>
3 #include <string>
4 #include <cstdio>
5 using namespace std;
6 const int N=5;
7 int map[10][10];//邻接矩阵
8 int screen[N][N];//屏幕最后显示的内容
9 string cover[N][N];//能覆盖(i,j)位置的窗口
10 string s;
11 int vis[10];//标记
12 int id[10];//入度
13 int t;//记录出现的窗口种类数
14
15 void cal()//初始化cover
16 {
17 int k,i,j;
18 for(i=0;i<N;i++)
19 for(j=0;j<N;j++)
20 cover[i][j].erase();
21 for(k=1;k<=9;k++)
22 {
23 i=(k-1)/3;
24 j=(k-1)%3;
25 cover[i][j]+=(char)(k);
26 cover[i][j+1]+=(char)(k);
27 cover[i+1][j]+=(char)(k);
28 cover[i+1][j+1]+=(char)(k);
29 }
30 }
31
32 void build()//构造有向图
33 {
34 int i,j,k;
35 for(i=0;i<N-1;i++)
36 {
37 for(j=0;j<N-1;j++)
38 {
39 for(k=0;k<cover[i][j].length();k++)
40 {
41 if((!map[screen[i][j]][cover[i][j][k]]) && (screen[i][j]!=cover[i][j][k]))
42 {
43 map[screen[i][j]][cover[i][j][k]]=1;
44 id[cover[i][j][k]]++;
45 }
46 }
47 }
48 }
49 }
50
51 int topo()//拓扑排序,判环
52 {
53 int i,j,k;
54 for(i=0;i<t;i++)
55 {
56 k=1;
57 while(!vis[k] || (k<=9&&id[k]>0))
58 k++;
59 if(k>9)
60 return 0;
61 vis[k]=0;
62 for(j=1;j<10;j++)
63 {
64 if(vis[j]&&map[k][j])
65 id[j]--;
66 }
67 }
68 return 1;
69 }
70
71 int main()
72 {
73 int i,j,k;
74 cal();
75 while(cin>>s)
76 {
77 if(s=="ENDOFINPUT")
78 break;
79 memset(id,0,sizeof(id));
80 memset(vis,0,sizeof(vis));
81 memset(map,0,sizeof(map));
82 t=0;
83 for(i=0;i<N-1;i++)
84 {
85 for(j=0;j<N-1;j++)
86 {
87 scanf("%d",&k);
88 if(!vis[k])
89 {
90 t++;
91 vis[k]=1;
92 }
93 screen[i][j]=k;
94 }
95 }
96 build();
97 if(topo())
98 puts("THESE WINDOWS ARE CLEAN");
99 else
100 puts("THESE WINDOWS ARE BROKEN");
101 cin>>s;
102 }
103 return 0;
104 }



