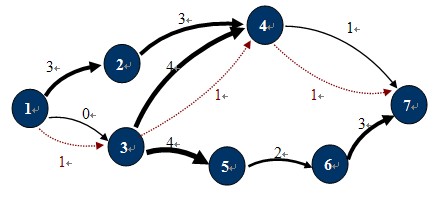
图1
如图-1所示,在这个运输网络中,源点S和汇点T分别是1,7,各边的容量为C(u,v)。图中红色虚线所示就是一个可行流。标准图示法如图-2所示:
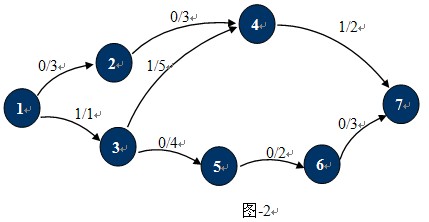
其中p(u,v) / c(u,v)分别表示该边的实际流量与最大容量。
关于最大流
熟悉了什么是网络流,最大流也就很好理解了。就是对于任意的u∈V-{s},使得p(s,u)的和达到最大。上面的运输网络中,最大流如图-3所示:MaxFlow=p(1,2)+p(1,3)=2+1=3。
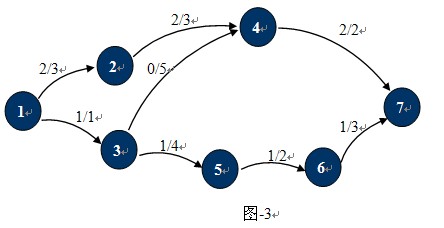
在介绍最大流问题之前,先介绍几个概念:残余网络,增广路径,反向弧,最大流定理以及求最大流的Ford-Fulkerson方法。
残余网络 增广路径 反向弧
观察下图-4,这种状态下它的残余网络如图-5所示:
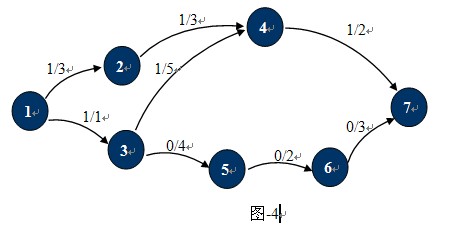
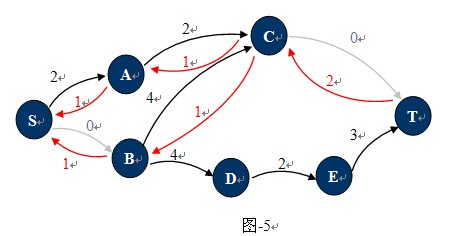
也许现在你已经知道什么是残余网络了,对于已经找到一条从S 到T的路径的网络中,只要在这条路径上,把C(u,v)的值更新为C(u,v)-P(u,v),并且添加反向弧C(v,u)。对应的增广路径Path为残留网络上从S到T的一条简单路径。图-4中1,2,4,7就是一条增广路径,当然还有1,3,4,7。
此外在未做任何操作之前,原始的有向图也是一个残余网络,它仅仅是未做任何更新而已。
最大流定理
如果残留网络上找不到增广路径,则当前流为最大流;反之,如果当前流不为最大流,则一定有增广路径。
Ford-Fulkerson方法
介绍完上面的概念之后,便可以用Ford-Fulkerson方法求最大流了。为什么叫Ford-Fulkerson方法而不是算法,原因在于可以用多种方式实现这一方法,方式并不唯一。下面介绍一种基于广度优先搜索(BFS)来计算增广路径P的算法:Edmonds-Karp算法。
算法流程如下:
设队列Q:存储当前未访问的节点,队首节点出队后,成为已检查的标点;
Path数组:存储当前已访问过的节点的增广路径;
Flow数组:存储一次BFS遍历之后流的可改进量;
Repeat:
Path清空;
源点S进入Path和Q,Path[S]<-0,Flow[S]<-+∞;
While Q非空 and 汇点T未访问 do
Begin
队首顶点u出对;
For每一条从u出发的弧(u,v) do
If v未访问 and 弧(u,v) 的流量可改进;
Then Flow[v]<-min(Flow[u],c[u][v]) and v入队 and Path[v]<-u;
End while
If(汇点T已访问)
Then 从汇点T沿着Path构造残余网络;
Until 汇点T未被访问
模版题:
POJ 1273 Drainage Ditches
代码:
 View Code
View Code 1 #include <iostream>
2 #include <cstdio>
3 #include <cstring>
4 #include <queue>
5 using namespace std;
6 const int N=210;
7 const int INF=0x7FFFFFFF;
8 int n,m,map[N][N],path[N],flow[N],start,end;
9 queue<int> q;
10 int bfs()
11 {
12 int i,t;
13 while(!q.empty())
14 q.pop();
15 memset(path,-1,sizeof(path));
16 path[start]=0,flow[start]=INF;
17 q.push(start);
18 while(!q.empty())
19 {
20 t=q.front();
21 q.pop();
22 if(t==end)
23 break;
24 for(i=1;i<=m;i++)
25 {
26 if(i!=start&&path[i]==-1&&map[t][i])//找到新节点i
27 {
28 //路径上的最小残量
29 flow[i]=flow[t]<map[t][i]?flow[t]:map[t][i];
30 q.push(i);//记录i的父亲,并加入FIFO队列
31 path[i]=t;
32 }
33 }
34 }
35 if(path[end]==-1)
36 return -1;
37 return flow[m];//一次遍历之后的流量增量
38 }
39 int Edmonds_Karp()
40 {
41 int max_flow=0,step,now,pre;
42 while((step=bfs())!=-1)
43 {//找不到增广路径时退出
44 max_flow+=step;
45 now=end;
46 while(now!=start)
47 {
48 pre=path[now];
49 map[pre][now]-=step;//更新正向边的实际容量
50 map[now][pre]+=step;//添加反向边
51 now=pre;
52 }
53 }
54 return max_flow;
55 }
56 int main()
57 {
58 int i,u,v,cost;
59 while(~scanf("%d%d",&n,&m))
60 {
61 memset(map,0,sizeof(map));
62 for(i=0;i<n;i++)
63 {
64 scanf("%d%d%d",&u,&v,&cost);
65 map[u][v]+=cost;
66 }
67 start=1,end=m;
68 printf("%d\n",Edmonds_Karp());
69 }
70 return 0;
71 }
72
2 #include <cstdio>
3 #include <cstring>
4 #include <queue>
5 using namespace std;
6 const int N=210;
7 const int INF=0x7FFFFFFF;
8 int n,m,map[N][N],path[N],flow[N],start,end;
9 queue<int> q;
10 int bfs()
11 {
12 int i,t;
13 while(!q.empty())
14 q.pop();
15 memset(path,-1,sizeof(path));
16 path[start]=0,flow[start]=INF;
17 q.push(start);
18 while(!q.empty())
19 {
20 t=q.front();
21 q.pop();
22 if(t==end)
23 break;
24 for(i=1;i<=m;i++)
25 {
26 if(i!=start&&path[i]==-1&&map[t][i])//找到新节点i
27 {
28 //路径上的最小残量
29 flow[i]=flow[t]<map[t][i]?flow[t]:map[t][i];
30 q.push(i);//记录i的父亲,并加入FIFO队列
31 path[i]=t;
32 }
33 }
34 }
35 if(path[end]==-1)
36 return -1;
37 return flow[m];//一次遍历之后的流量增量
38 }
39 int Edmonds_Karp()
40 {
41 int max_flow=0,step,now,pre;
42 while((step=bfs())!=-1)
43 {//找不到增广路径时退出
44 max_flow+=step;
45 now=end;
46 while(now!=start)
47 {
48 pre=path[now];
49 map[pre][now]-=step;//更新正向边的实际容量
50 map[now][pre]+=step;//添加反向边
51 now=pre;
52 }
53 }
54 return max_flow;
55 }
56 int main()
57 {
58 int i,u,v,cost;
59 while(~scanf("%d%d",&n,&m))
60 {
61 memset(map,0,sizeof(map));
62 for(i=0;i<n;i++)
63 {
64 scanf("%d%d%d",&u,&v,&cost);
65 map[u][v]+=cost;
66 }
67 start=1,end=m;
68 printf("%d\n",Edmonds_Karp());
69 }
70 return 0;
71 }
72










