二叉树以及常见面试题

一、什么是二叉树

　　二叉树是每个结点最多有两个子树的树结构，二叉树是递归定义的，其结点有左右子树之分，通常包含：满二叉树、完全二叉树、霍夫曼树、平衡二叉树、红黑树等。

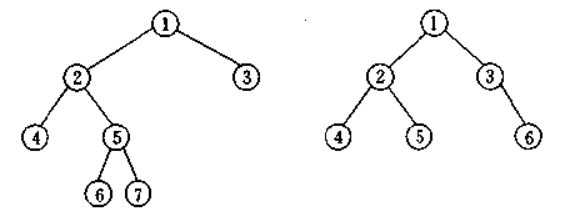
　　满二叉树：如果二叉树中所有分支结点的度数都为2，并且叶子结点都在统一层次上，则二叉树为满二叉树，从图形形态上看，满二叉树外观上是一个三角形；从数学上看，满二叉树的各个层的结点数形成一个首项为1，公比为2的等比数列。如图：

　　完全二叉树：完全二叉树从根结点到倒数第二层满足满二叉树，最后一层可以不完全填充，其叶子结点都靠左对齐。满二叉树一定是完全二叉树，完全二叉树不一定是满二叉树。

　　非完全二叉树：

二、二叉树常见的问题

本文包括：

2.1 二叉树的创建

2.2 二叉树的遍历

2.3 求叶子节点的个数

2.4 求树的深度

2.5 交换树的左右子树

2.6 判断一个节点是否在一棵子树中

2.7 求树中总共的节点个数

2.8 判断两个树是否相同

2.9 判断一个树是否为另一棵树的子树

2.1 二叉树的创建

　　参考代码：https://www.cnblogs.com/BeyondAnyTime/archive/2012/08/27/2659163.html

#include <QCoreApplication>
#include <QDebug>
#include <QTextStream>
//二叉树的节点
class BinTreeNode
{
private:
    int data;
    BinTreeNode *left,*right;
public:
    //利用初始化列表完成data、left、right的初始化
    BinTreeNode(const int &item,BinTreeNode *lPtr = NULL,BinTreeNode *rPtr = NULL):data(item) ,left(lPtr),right(rPtr){}
    void set_data(int item)
    {
        data = item;
    }
    int get_data()const
    {
        return data;
    }
    void set_left(BinTreeNode *l)
    {
        left = l;
    }
    BinTreeNode *get_left() const
    {
        return left;
    }
    void set_right(BinTreeNode *r)
    {
        right = r;
    }
    BinTreeNode *get_right() const
    {
        return right;
    }
};
//二叉树
class BinTree
{
private:
    BinTreeNode *root;
public:
    BinTree(BinTreeNode *t = NULL):root(t){}
    ~BinTree(){delete root;}
    void set_root(BinTreeNode *t)
    {
        root = t;
    }
    BinTreeNode *get_root() const
    {
        return root;
    }

    //创建二叉树
    BinTreeNode * create_tree();

};
BinTreeNode *BinTree::create_tree()
{
    QString item;
    BinTreeNode *t,*t_l,*t_r;
    QTextStream qin(stdin);
    qin>>item;
    int data = item.toInt();

    if(item != "#")
    {
        BinTreeNode *pTmpNode = new BinTreeNode(data);
        t = pTmpNode;
        t_l = create_tree();
        t->set_left(t_l);
        t_r = create_tree();
        t->set_right(t_r);
        return t;
    }
    else
    {
        t = NULL;
        return t;
    }
}

int main(int argc, char *argv[])
{
    QCoreApplication a(argc, argv);

    BinTree tree;
    qDebug()<<"输入二叉树前序序列进行建树，\"#\"代表空节点"<<endl;
    tree.set_root(tree.create_tree());

    return a.exec();
}

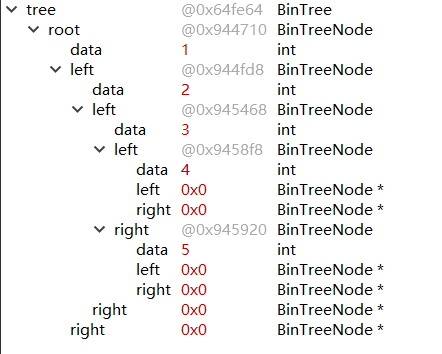
　　由此，可以看到，其实构造一个二叉树并不是一个十分困难的过程，当然我们采用的是先序创建。结合自己的想法很容易写出二叉树：

#include <QCoreApplication>
#include <QDebug>
#include <QTextStream>

class binTreeTest
{
public:
    int data;
    binTreeTest *left,*right;
    void setData(int item)
    {
        data = item;
    }
    int getData()
    {
        return data;
    }
    void set_left(binTreeTest *l)
    {
        left = l;
    }
    binTreeTest * get_left()const
    {
        return left;
    }
    void set_right(binTreeTest *r)
    {
        right = r;
    }
    binTreeTest * get_right()const
    {
        return right;
    }

};
void createBinTree(binTreeTest **r)
{
    QString item;
    QTextStream qin(stdin);
    qin>>item;
    int data = item.toInt();
    binTreeTest *T_l,*T_r;
    if(item != "#")
    {
        (*r)->setData(data);
        T_l = new binTreeTest;
        T_r = new binTreeTest;
        createBinTree(&T_l);
        (*r)->set_left(T_l);

        createBinTree(&T_r);
        (*r)->set_right(T_r);
    }
    else
    {
        *r = NULL;
    }
}
int main(int argc, char *argv[])
{
    QCoreApplication a(argc, argv);

    binTreeTest *tree = new binTreeTest;
    qDebug()<<"输入二叉树前序序列进行建树，\"#\"代表空节点"<<endl;
    createBinTree(&tree);
    return a.exec();
}

　　在使用的过程中，注意C++的使用：https://www.cnblogs.com/pinking/p/9339201.html。

2.2 二叉树的遍历

　　二叉树的遍历分为两种策略：深度优先和广度优先，深度优先又包含：中序遍历、前序遍历、后序遍历。记忆的时候就看中间那个是什么就是什么序的遍历。

　　中序遍历：左子树---> 根结点 ---> 右子树

　　前序遍历：根结点 ---> 左子树 ---> 右子树

　　后序遍历：左子树 ---> 右子树 ---> 根结点

　　层次遍历：仅仅需按层次遍历就可以

　　构造二叉树如图：

　　输入构造二叉树：

　　中序遍历代码：

void middle(binTreeTest *t)
{

    if(t != NULL)
    {
        binTreeTest *l,*r;
        l = t->get_left();
        middle(l);
        qDebug()<<t->getData();
        r = t->get_right();
        middle(r);
    }
}

　　中序遍历输出结果：

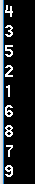
　　同理，前序遍历应该的结果为：1、2、3、4、5、6、7、8、9 。代码如下：

1 void forward(binTreeTest *t)
2 {
3     if(t != NULL)
4     {
5         qDebug()<<t->getData();
6         forward(t->get_left());
7         forward(t->get_right());
8     }
9 }

View Code

　　后序遍历的结果应该为：4、5、3、2、8、9、7、6、1 。代码如下：

1 void backward(binTreeTest *t)
2 {
3     if(t != NULL)
4     {
5         backward(t->get_left());
6         backward(t->get_right());
7         qDebug()<<t->getData();
8     }
9 }

View Code

　　层次遍历，通常采用队列的形式，保持先进先出的方式，层次遍历每一层，结果为：1、2、6、3、7、4、5、8、9 。代码如下：

 1 void level(binTreeTest *t)
 2 {
 3     if(t == NULL)
 4         return;
 5     QQueue<binTreeTest*> queue;
 6     queue.enqueue(t);
 7     while (!queue.empty())
 8     {
 9         binTreeTest *ptem = queue.front();
10         qDebug()<<ptem->getData();
11         queue.pop_front();
12         if(ptem->get_left() != NULL)
13         {
14             queue.push_back(ptem->get_left());
15         }
16         if(ptem->get_right() != NULL)
17         {
18             queue.push_back(ptem->get_right());
19         }
20     }
21 }

View Code

2.3 求叶子节点的个数

　　求叶子节点的个数还是比较好理解的，代码如下：

int get_leaf_num(binTreeTest *t)
{
    if(t == NULL)
        return 0;
    if(t->get_left() == NULL && t->get_right() == NULL)
    {
        return 1;
    }
    return get_leaf_num(t->get_left())+get_leaf_num(t->get_right());
}

2.4 求树的深度

int getTreeHeight(binTreeTest *t)
{
    if (t == NULL)
        return 0;
    if(t->get_left() == NULL && t->get_left() == NULL)
    {
        return 1;
    }
    int l_height = getTreeHeight(t->get_left());
    int r_height = getTreeHeight(t->get_right());
    return l_height>=r_height?l_height+1:r_height+1;
}

2.5 交换树的左右子树

void swap_tree(binTreeTest *t)
{
    if(t == NULL)
        return;
    binTreeTest *temp = new binTreeTest;
    temp = t->get_right();
    t->set_right(t->get_left());
    t->set_left(temp);

    swap_tree(t->get_left());
    swap_tree(t->get_right());
}

2.6 判断一个节点是否在一棵子树中

　　其实思想和遍历是一样的，代码如下：

bool isInTree(binTreeTest *tree,binTreeTest *nodeTree)
{
    //查找的节点为NULL时，代表没有查到
    if(tree == NULL)
        return false;
    else if(tree->getData() == nodeTree->getData())
    {
        return true;
    }
    else
    {
        bool has = false;
        if(tree->get_left() != NULL)
        {
            has = isInTree(tree->get_left(),nodeTree);
        }
        if((has == false) && (tree->get_right() != NULL))
        {
            has = isInTree(tree->get_right(),nodeTree);
        }
        return has;
    }
}

2.7 求树中总共的节点个数

int getNumNode(binTreeTest *t)
{
    if(t == NULL)
        return 0;
    return getNumNode(t->get_left())+getNumNode(t->get_right())+1;
}

2.8 判断两个树是否相同

bool compared(binTreeTest *tree,binTreeTest *tree2)
{
    //两个树都是空
    if(tree == NULL && tree2 == NULL)
        return true;
    if(tree == NULL || tree2 == NULL)//其中有一个为NULL就不用比了
        return false;
    if(tree->getData() == tree2->getData())
    {
        return compared(tree->get_left(),tree2->get_left())&&compared(tree->get_right(),tree2->get_right());
    }
    else
    {
        return false;
    }
}

2.9 判断一个树是否为另一棵树的子树

　　这个需要结合上面的判断两棵树是否相同来判断：

bool compared(binTreeTest *tree,binTreeTest *tree2)
{
    //两个树都是空
    if(tree == NULL && tree2 == NULL)
        return true;
    if(tree == NULL || tree2 == NULL)//其中有一个为NULL就不用比了
        return false;
    if(tree->getData() == tree2->getData())
    {
        return compared(tree->get_left(),tree2->get_left())&&compared(tree->get_right(),tree2->get_right());
    }
    else
    {
        return false;
    }
}
bool judgeNode(binTreeTest *tree,binTreeTest *child)
{
    // 两个都是空树
    if(tree == NULL && child == NULL)
        return true;
    // 空树是任意的子树
    if(child == NULL)
        return true;
    // 空树没有其他非空的子树
    if(tree  == NULL)
        return false;
    //排除空树的情况
    if(tree->getData() == child->getData())
    {
        return compared(tree,child);
    }
    else
    {
        bool result = judgeNode(tree->get_left(),child);
        if(result == false)
            return judgeNode(tree->get_right(),child);
        return result;
    }
}

posted on 2018-07-19 20:52 禅在心中阅读(5177) 评论(0) 编辑收藏举报