参数估计

简单的讨论一下参数估计理论

一、什么是参数估计

　　参数通常用来表示一个量，可以是标量也可以是有值向量。按照时间变化，也可以分为时常参数和时变参数。对于时常参数的估计称为参数估计。对于时变的参数估计称为状态估计，本文不研究。参数估计的包括两个主要的模型以及四个基本估计方法，如下图所示：

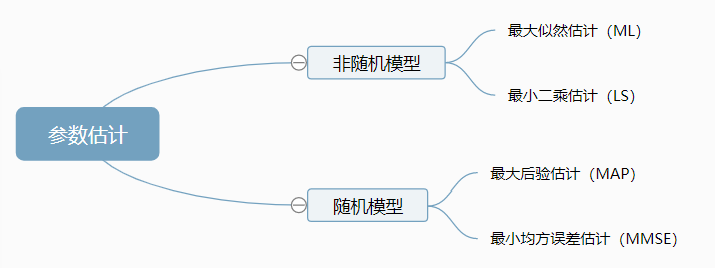
　　贝叶斯学派和频率学派最大的不同、根上的不同，就是在于模型 y=wx+b 其中的 w 和 b 两个参数，频率学派认为参数是固定的、也就是上面的非随机模型，只要通过不停的采样、不停的观测训练，就能够估算参数 w 和 b，因为它们是固定不变的；而贝叶斯学派相反，他们认为这些参数是变量，它们是服从一定的分布的，也就是上面的随机模型，这是它最根本的差别。通常上面两种也被称为点估计和区间估计。

二、四种基本的估计方法

2.1  最大似然估计

　　使得似然函数达到最大的x即为参数x的ML估计：

2.2  最小二乘估计

（我还是直接抄书吧。。。以下以上都来自《雷达数据处理及应用》）

 

2.3  最大后验估计

　　对于随机参数，由于已知其先验概率p（x），由贝叶斯准则：

　　可以求得其后验概率密度函数，使后验概率密度函数最大的x被称为参数x的最大后验估计，即：

2.4  最小均方误差估计

三、最大似然估计和最小二乘估计的对比

　　当模型是高斯分布时，最大似然估计和最小二乘估计是等价的。