对于条件随机场的学习,我觉得应该结合HMM模型一起进行对比学习。首先浏览HMM模型:https://www.cnblogs.com/pinking/p/8531405.html
一、定义
条件随机场(crf):是给定一组输入随机变量条件下,另一组输出随机变量的条件概率的分布模型,其特点是假设输出随机变量构成马尔科夫随机场。本文所指线性链条件随机场。
隐马尔科夫模型(HMM):描述由隐藏的马尔科夫链随机生成观测序列的过程,属于生成模型。
当然,作为初学者,从概念上直观感受不到两者的区别与联系,甚至感觉两个概念都理解不了了,不过这没啥问题,继续学下去吧。
二、学习CRF包含的知识点
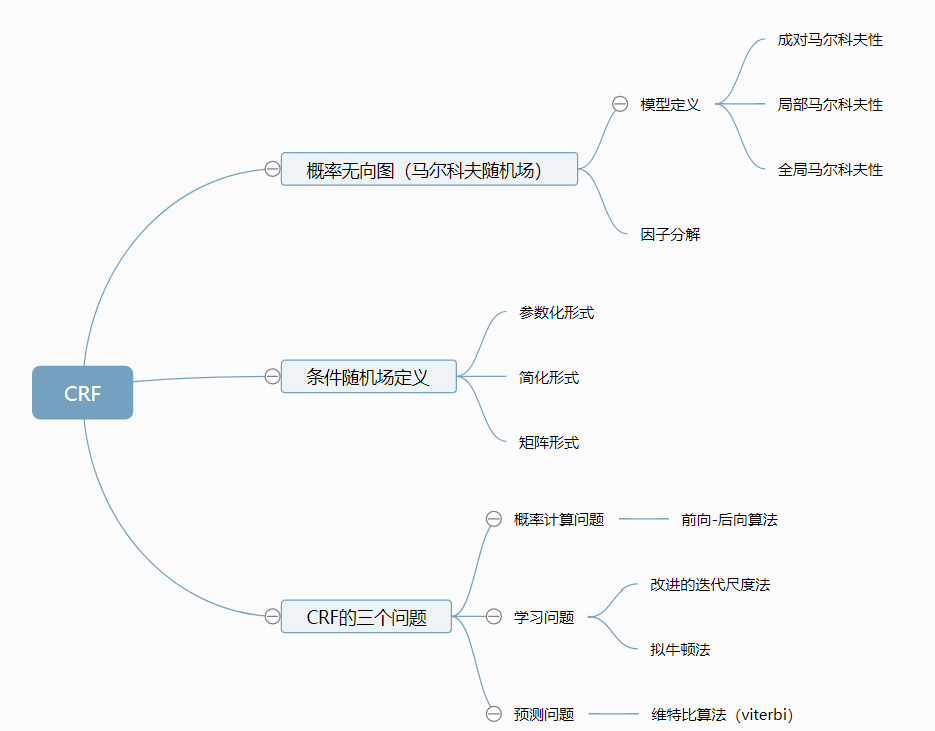
参考李航的统计学习方法,将该部分内容的主要知识点梳理如图,可以看到,CRF和HMM由很多共同点,譬如,都和马尔科夫有关、都有三个问题要解决,解决的方法也有相同的地方。
三、概率无向图
概率无向图,又称马尔科夫随机场,也就是定义中假设输出随机变量构成的。关于模型的构建,其实就是一个由节点(node,记作V)和节点链接关系的边(edge,记作E)组成的图G = (V,E),所谓无向图,就是边没有方向。
随机变量存在的关系包括:成对马尔科夫性、局部马尔科夫性和全局马尔科夫性。假设随机变量的联合概率分布P(Y)和表示它的无向图G,若P(Y)满足上述三种关系,则此联合概率分布为概率无向图或称为马尔科夫随机场。
提出该定义事实上是为了求联合概率分布做铺垫,为了求联合概率,给出无向图中的团与最大团的定义。
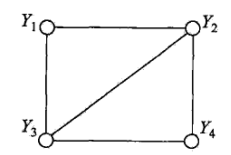
团:{Y1,Y2},{Y1,Y3},{Y2,Y3},{Y2,Y4},{Y3,Y4}
最大团:{Y1,Y2,Y3},{Y4,Y2,Y3}
概率无向图模型的联合概率分布表示为其最大团上的随机变量的函数的乘积的形式的操作。概率无向图模型的链和概率分布P(Y)可以表示为如下形式:

C为无向图的最大团,Yc是C的结点对应的随机变量,Ψ就是一个函数,暂且不用管是什么,就是一个转换关系。
看到这里,其实对于CRF的结果的图的理解已经有了铺垫,实际上,CRF就是将输入X,经过变换,获得输出Y的过程,当然这个Y就满足了上面所画的无向图。但是这个概率是干什么的呢?
继续看CRF的内容,等看完再第四章返回来看该处内容,我相信会有进一步了解,知道概率是怎么求的了吧。
四、条件随机场的定义
突然来的一点感悟,和内容无关:虽然这一章和第一章内容有点重合,但是我觉得作为初学者,最应该的是一个循序渐进的过程,有很多书都是为了内容的连续性,而忽略初学者的接受能力,事实上很多东西需要不断学习,不断深入的过程,这个在很多教程并不能体现出来,而且有时候,网上查问题找资料,总是一搜一大堆,一打开都是一样的,可能是很多人看到别人的博客,学习完了,理解了然后就复制粘贴上了,也懒得再改改或者加点自己的东西。我觉得是可以理解的,最好百度能做一个机制,相同的东西别都索引上了。
条件概率模型:P(Y|X),Y为输出变量,表示标记的序列,X为输入变量,表示需要标注的观测序列(再HMM中也称为状态序列)。
- 学习问题中,利用极大似然估计,估计P^(Y|X)
- 预测问题中,利用给定的序列x,求出条件概率P^(Y|X)最大的输出序列y^
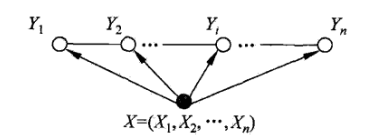
一般的线性链条件随机场表示如图,通常假设X和Y有相同的结构,那么表示图就如下所示:
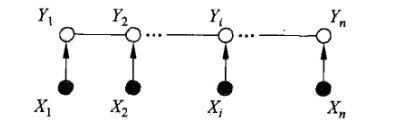
而此时,最大团,就是相邻两个结点的集合。可以引出公式:
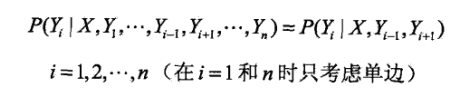
当然,后续会有CRF的参数化形式、简化形式等表示形式,但实际上都是第三章求概率的表达。
五、CRF的三个需要解决的问题
5.1 概率计算问题
条件随机场的概率计算问题,就是给定x,y,求它的P(Yi = yi | x),P(Yi-1 = yi-1 ,Yi = yi | x)以及相应的数学期望的问题。其解决手段用的是HMM那样的前向-后向算法。
前向-后向算法:
定义前向向量:ai(x):
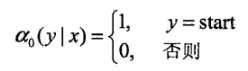
递推公式表示为:
![]()
ai(yi|x)表示在位置i的标记为yi并且到位置i的前部分标记序列的非规范化概率,yi可取m个,所以ai(x)是m维列向量。同理也可以定义后向算法。其中M的定义是在上述条件随机场的矩阵形式中定义的,本文中未介绍,直接给出定义:
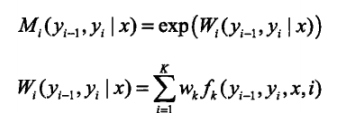
Mi表示的是随机变量Y取值为yi的非规范化的条件概率,这个概率依赖于当前和前一个位置。
对于此处的理解,我觉得如果非要和HMM中类比的化,a类似于前向概率,只不过此处叫做:前向向量,两者的不同就是在CRF中,a的求法没有状态转移矩阵;而M类似于HMM中状态转移概率位置。并且,CRF的这个式子中,没有观测矩阵。总之虽然都叫前向求法,但是里面参数意义是不一样的,不好对比,CRF中,并不是依赖状态转移矩阵和观测矩阵的过程,而是一个依赖于前一时刻生成结果的概率的预测概率。因为我们要计算的是一个已知yi排列的概率嘛,所以是一个连乘的关系,按序列顺序将概率相乘(i时刻的概率依赖于i-1时刻的概率)。
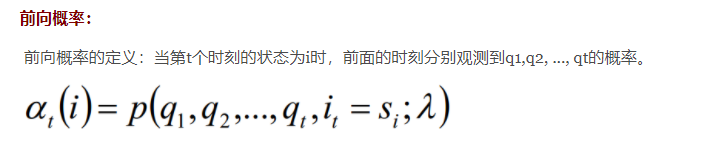
后向向量,表示在位置i的标记为yi并且从i+1到n的后部分标记序列的非规范化概率。
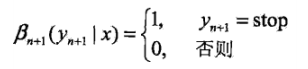
![]()
当然,前向向量是从前往后扫描,扫到头的化,就和后向向量第一个值相同了。。。
![]()
概率计算:
按照前向-后向向量的定义,可知,αi表示位置i处标记为yi,从1到i-1处为某一排列的概率,βi表示位置i处标记为yi,从i+1到n处为某一排列的概率。因此,得到条件概率:
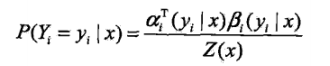
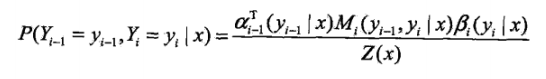
对于下面一个式子的理解:事实上,这两个概率都是根据定义直接列出来的,αi-1表示i-1标记为yi-1时,以及之前排序为某一序列的概率,因为yi-1与yi并不是独立的,所以联合概率就表示成上面的式子了。
期望值的计算:
利用前向-后向算法,可以求出特征函数fk关于P(X,Y)和P(Y|X)的数学期望。不过要求P(X , Y)的话,需要假设经验分布P^(X)。该期望值的计算公式此处略过,就是一个求期望的公式嘛。
5.2 条件随机场的学习算法
该节研究的是给定训练数据集估计CRF模型参数的问题。参数估计通常用极大似然估计,HMM中,如果隐层状态未知的话,也是用极大似然估计。
具体的优化实现算法有改进的迭代尺度法IIS、梯度下降法以及拟牛顿法。直接给出优化函数吧:
![]()
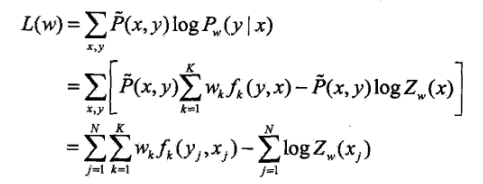
其实就是一个EM算法,道理和HMM中的一样,先对权值w进行优化,优化完求状态特征和转移特征的期望,然后再根据期望再迭代优化w,最后满足概率最大就可以了。
5.3 条件随机场的预测算法
条件随机场的预测问题,是给定CRF和输入x,求输出y的问题。这个求法就是使用viterbi算法。求法同HMM一样,只不过HMM中反推的时候,利用的是上一时刻某一状态转移到当前时刻状态概率最大的那个上一时刻的状态。
此处,结合序列标记问题,定义为δi(l),表示在位置i标记l各个可能取值(1,2...m),递推公式:
![]()
![]()
其中,![]() 就是非规范化的P(yi|x),因此,这里采用了相加的方法。反推的时候,选择上一时刻某一Ψ,在李航书中那个例子的观察方法如下,其中画黄框的是取值大的那一项。
就是非规范化的P(yi|x),因此,这里采用了相加的方法。反推的时候,选择上一时刻某一Ψ,在李航书中那个例子的观察方法如下,其中画黄框的是取值大的那一项。
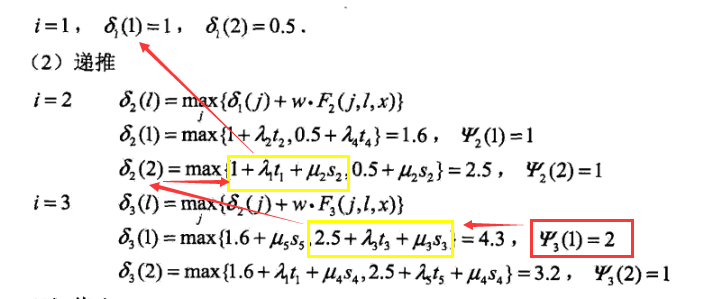
六、CRF与HMM的区别联系
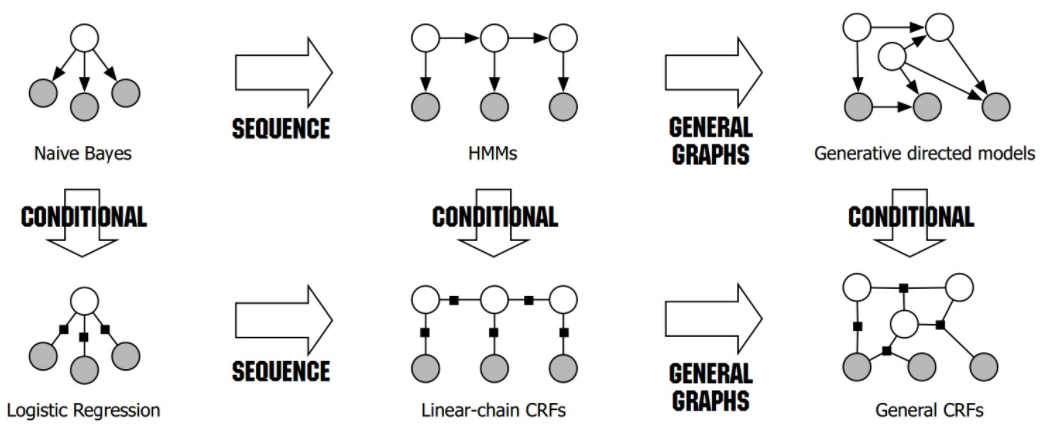
来自:Sutton, Charles, and Andrew McCallum. "An introduction to conditional random fields." Machine Learning 4.4 (2011): 267-373.
虽然网上这个图都在抄,不过我感觉都解释的不够详细啊。首先从HMM看,白色圆代表状态,黑色代表观测值,可以看到,他们之间有一个顺序的依赖关系;而采用CRF的话,状态和观测值(或者说用词性和词语表示),可以看到没有这种顺序的依赖关系。HMM中的状态只与前一个有关,而CRF综合考虑了前后的依赖关系。
判别式模型和生成式模型
HMM是生成式模型,CRF是判别式模型,首先介绍两种模型。判别模型是给定输入序列 X,直接评估对应的输出Y ;生成模型是评估给定输出 Y,如何从概率分布上生成输入序列 X。其实两者的评估目标都是要得到最终的类别标签Y, 即Y=argmax p(y|x)。判别式模型直接通过解在满足训练样本分布下的最优化问题得到模型参数,主要用到拉格朗日乘算法、梯度下降法,常见的判别式模型如最大熵模型、CRF、LR、SVM等;而生成式模型先经过贝叶斯转换成Y = argmax p(y|x) = argmax p(x|y)*p(y),然后分别学习p(y)和p(x|y)的概率分布,常见的如n-Gram、HMM、Naive Bayes。
判别模型和生成模型只是描述一种问题的两种方式,在理论上,它们是可以互相转换的。 对于上述HMM和CRF的区别,最主要的就是对于HMM,需要加入状态概率分布的先验知识,即:
![]()
在HMM中有这样一个过程,但是CRF就不需要了。
最大后验估计 vs最大似然估计
- 频率学派:最大似然估计(MLE):在进行推论时,我们只关心似然度,并选择给出所最大化 p(data|hypo) 的假设作为预测。
- 贝叶斯学派:最大后验估计(MAP):我们也需要把先验 p(hypo) 纳入计算,不仅是似然度,还要选择给出最大 p(data|hypo) * p(hypo) 的假设作为预测。
- 如果我们认为所有假设都服从均匀分布,那么MAP = MLE 。
可以看到,HMM和CRF是两种思路,CRF是频率学派,而HMM是贝叶斯学派的。
七、CRF与Softmax
对于序列标注问题,可以简单的理解为分类问题,既然是分类,为什么NLP中通常不直接用softmax等分类器,而使用CRF\HMM呢?这是因为目标输出序列本身会带有一些上下文关联,而softmax等不能体现出这种联系。当然,CRF体现的不仅仅是上下文的联系,更重要的是利用viterbi算法,体现的是一种路径规划的概率。
另外,通常在NLP中,输入每个batch的语句长度是不一样的(单个batch语句长度可以通过padding补齐),如果用CNN做特征提取的话,batch之间的结果的维度是不同的。而采用CRF的话,就不用考虑这个维度不同的问题了。
softmax在tf中的接口:
@tf_export("nn.sampled_softmax_loss")
def sampled_softmax_loss(weights,
biases,
labels,
inputs,
num_sampled,
num_classes,
num_true=1,
sampled_values=None,
remove_accidental_hits=True,
partition_strategy="mod",
name="sampled_softmax_loss",
seed=None):
#num_sampled则是Sample Softmax时候用到的一个超参数,确定选几个词来对比优化
'''
weights: A `Tensor` of shape `[num_classes, dim]`, or a list of `Tensor`
objects whose concatenation along dimension 0 has shape
[num_classes, dim]. The (possibly-sharded) class embeddings.
biases: A `Tensor` of shape `[num_classes]`. The class biases.
labels: A `Tensor` of type `int64` and shape `[batch_size,
num_true]`. The target classes. Note that this format differs from
the `labels` argument of `nn.softmax_cross_entropy_with_logits`.
inputs: A `Tensor` of shape `[batch_size, dim]`. The forward
activations of the input network.
num_sampled: An `int`. The number of classes to randomly sample per batch.
num_classes: An `int`. The number of possible classes.
'''
而crf的接口:
def crf_log_likelihood(inputs,
tag_indices,
sequence_lengths,
transition_params=None):
"""Computes the log-likelihood of tag sequences in a CRF.
Args:
inputs: A [batch_size, max_seq_len, num_tags] tensor of unary potentials
to use as input to the CRF layer.
tag_indices: A [batch_size, max_seq_len] matrix of tag indices for which we
compute the log-likelihood.
sequence_lengths: A [batch_size] vector of true sequence lengths.
transition_params: A [num_tags, num_tags] transition matrix, if available.
"""
可以看到,虽然两者都是实现分类的功能,但是实际上是不一样的,基于seq2seq的时候用softmax判断字典中是哪一个字,其softmax的输入是一个固定维度的向量,因为整个seq2seq是基于序列的。而CRF输入就需要句子的长度做内部处理,它本身是基于序列的。
八、条件随机场的tensorflow代码实现
参考:https://mp.weixin.qq.com/s/1KAbFAWC3jgJTE-zp5Qu6g
作者以骰子为例,假设了每次掷骰子之间会有一个相互依赖的关系,参考代码:https://www.cnblogs.com/pinking/p/9362966.html 的基础上进行修改即可:
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
TIME_STEPS = 15#20 # backpropagation through time 的time_steps
BATCH_SIZE = 1#50
INPUT_SIZE = 1 # x数据输入size
LR = 0.05 # learning rate
num_tags = 2
# 定义一个生成数据的 get_batch function:
def get_batch():
xs = np.array([[2, 3, 4, 5, 5, 5, 1, 5, 3, 2, 5, 5, 5, 3, 5]])
res = np.array([[0, 0, 1, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 0, 1]])
return [xs[:, :, np.newaxis], res]
# 定义 CRF 的主体结构
class CRF(object):
def __init__(self, n_steps, input_size, num_tags, batch_size):
self.n_steps = n_steps
self.input_size = input_size
self.num_tags = num_tags
self.batch_size = batch_size
self.xs = tf.placeholder(tf.float32, [None, self.n_steps, self.input_size], name='xs')
self.ys = tf.placeholder(tf.int32, [self.batch_size, self.n_steps], name='ys')
#将输入 batch_size x seq_length x input_size 映射到 batch_size x seq_length x num_tags
weights = tf.get_variable("weights", [self.input_size, self.num_tags])
matricized_x_t = tf.reshape(self.xs, [-1, self.input_size])
matricized_unary_scores = tf.matmul(matricized_x_t, weights)
unary_scores = tf.reshape(matricized_unary_scores, [self.batch_size, self.n_steps, self.num_tags])
sequence_lengths = np.full(self.batch_size,self.n_steps,dtype=np.int32)
log_likelihood,transition_params = tf.contrib.crf.crf_log_likelihood(unary_scores,self.ys,sequence_lengths)
self.pred, viterbi_score = tf.contrib.crf.crf_decode(unary_scores, transition_params, sequence_lengths)
# add a training op to tune the parameters.
self.cost = tf.reduce_mean(-log_likelihood)
self.train_op = tf.train.AdamOptimizer(LR).minimize(self.cost)
# 训练 CRF
if __name__ == '__main__':
# 搭建 CRF 模型
model = CRF(TIME_STEPS, INPUT_SIZE, num_tags, BATCH_SIZE)
sess = tf.Session()
sess.run(tf.global_variables_initializer())
# matplotlib可视化
plt.ion() # 设置连续 plot
plt.show()
# 训练多次
for i in range(150):
xs, res = get_batch() # 提取 batch data
#print(res.shape)
# 初始化 data
feed_dict = {
model.xs: xs,
model.ys: res,
}
# 训练
_, cost,pred = sess.run(
[model.train_op, model.cost, model.pred],
feed_dict=feed_dict)
# plotting
x = xs.reshape(-1,1)
r = res.reshape(-1, 1)
p = pred.reshape(-1, 1)
x = range(len(x))
plt.clf()
plt.plot(x, r, 'r', x, p, 'b--')
plt.ylim((-1.2, 1.2))
plt.draw()
plt.pause(0.3) # 每 0.3 s 刷新一次
# 打印 cost 结果
if i % 20 == 0:
print('cost: ', round(cost, 4))
得到的结果:
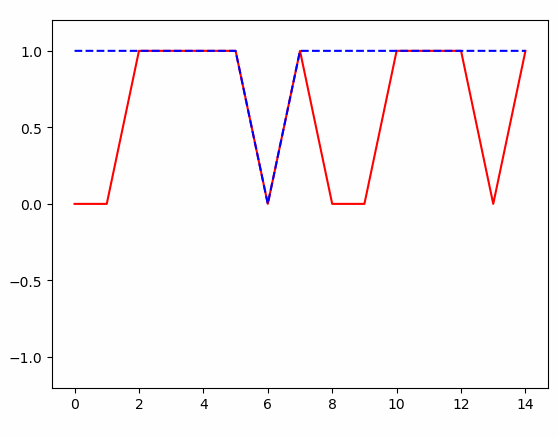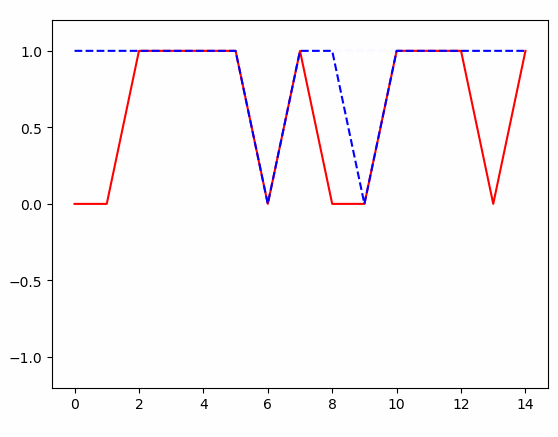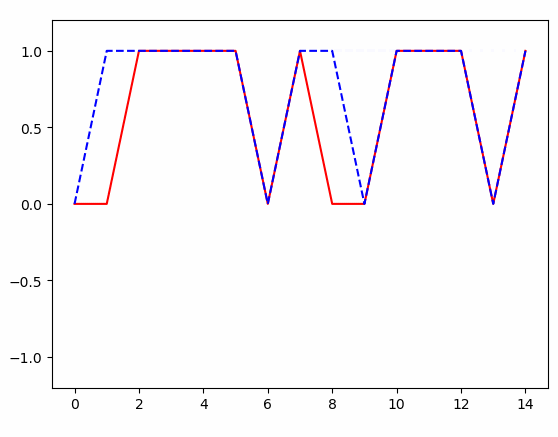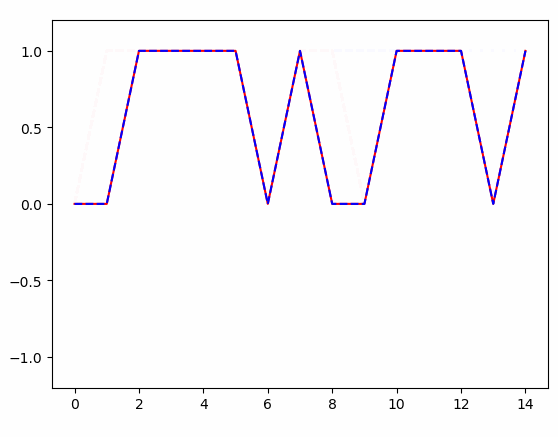
作者:禅在心中
出处:http://www.cnblogs.com/pinking/
本文版权归作者和博客园共有,欢迎批评指正及转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号