决策树（CART）

CART算法全称是分类回归算法，（Classification And Regression Tree），他与ID3、C4.5的不同在于：

1、既可以处理分类问题又可以处理回归问题

2、使用基尼系数作为分类依据，比起使用熵计算简单

3、使用的是二分递归分割的技术，生成二叉树

 

原理不在赘述，基尼系数计算公式：

其中，A表示某一属性，C表示这个属性下共C种特征，Pi表示第i个特征发生的概率

当然，对于公式解释的有点乱，很容易搞混，下面结合实例介绍如何计算：

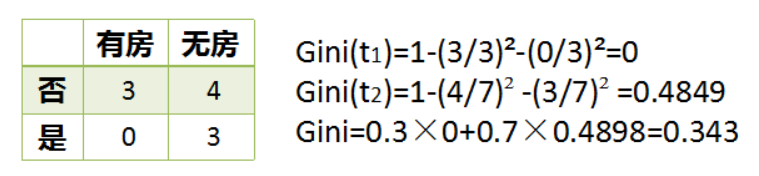
对于上面的属性，基尼系数计算如上所示。

对于信息增益的计算为：Gain(house) = Entropy(S) - 3/10*Entropy(has)-7/10*Entropy(nothas)

Entropy(S)  = -3/10*log(3/10)-7/10*log(7/10)

Entropy(has) = 0

Entropy(nothas) = -3/7*log(3/7)-4/7*log(4/7)

 

说白了，基尼系数和熵一样，也是衡量一个事件的不确定度。

故节点选择小的基尼系数的属性

 

对于Python代码，利用sklearn模块通常可以实现，

#   这里不写输入X和Y了，对应的例子有问题，待解决
from sklearn import tree
from sklearn.externals.six import StringIO
import pydotplus


clf = tree.DecisionTreeClassifier(criterion = 'gini')#算法模型

clf = clf.fit(X, Y)#模型训练
dot_data = StringIO()
tree.export_graphviz(clf, out_file=dot_data)
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
graph.write_pdf("test.pdf")#写入pdf

　　基本的程序如上，但是对于CART算法，输入的特征需要是实数，在这里需要进一步研究，有问题，待解决！！！