深度估计问题
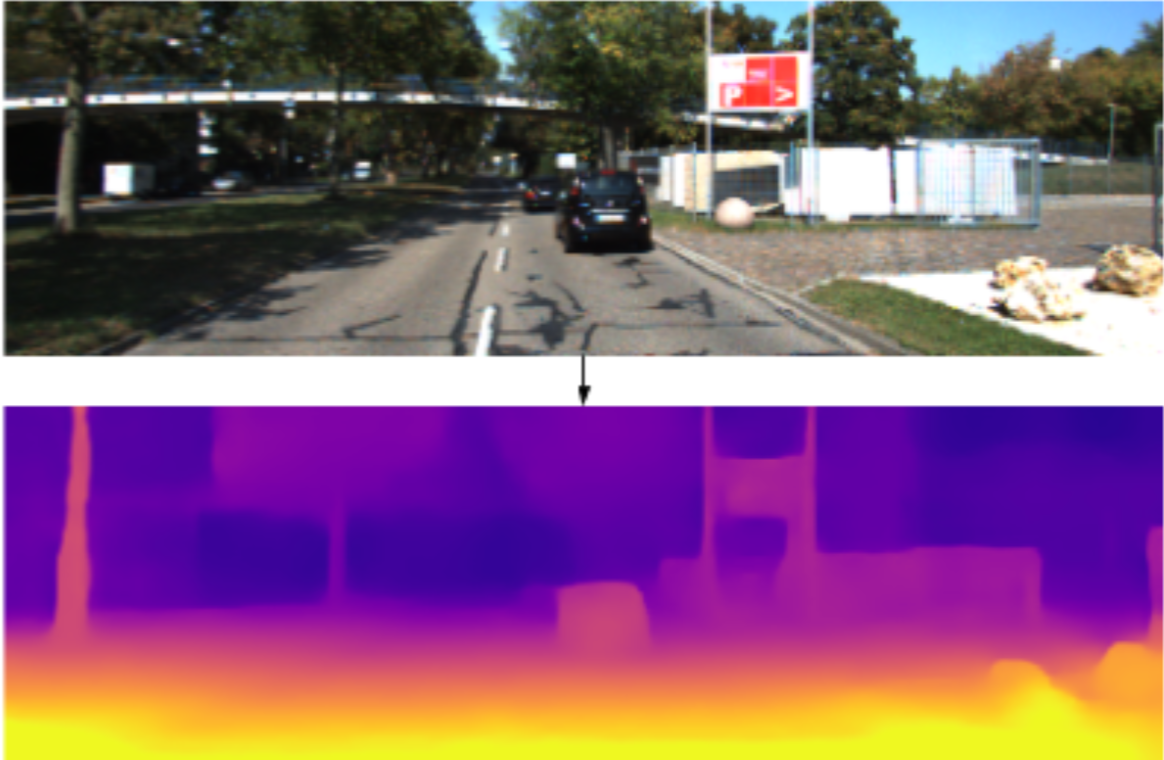
从输入的单目或双目图像，计算图像物体与摄像头之间距离（输出距离图），双目的距离估计应该是比较成熟和完善，但往单目上考虑主要还是成本的问题，所以做好单目的深度估计有一定的意义。单目的意思是只有一个摄像头，同一个时间点只有一张图片。就象你闭上一只眼睛，只用一只眼睛看这个世界的事物一样，距离感也会同时消失。
深度估计与语义分割的区别，及监督学习的深度估计问题
深度估计与语义分割有一定的联系，但也有一些区别。
- 图像的语义分割是识别每个像素的类别，不管这个像素出现在图像的那个位置，是一个分类任务。
- 而深度估计是识别每个像素与当前摄像头的距离，相同的车出现在图像的不同位置，其距离有可能不一样，是一个回归任务。
在深度估计上直接使用语义分割的方案，是可以达到一定的效果，但因为以上的区别，所以要把深度估计做好还是值得探讨。另外，
深度估计有监督学习的方案，但深度估计的监督学习存在两个问题：
- 监督学习所需要的label，制作上的代价比较大，不利于把方案应用到更多情境或验证；
- 如果以激光雷达的数据作为label，但激光雷达的探测距离比视觉近，一些超越探测距离的区域无法训练。
基于这些问题，本论文提出一种不需要真实深度label的自监督方法。
基本原理
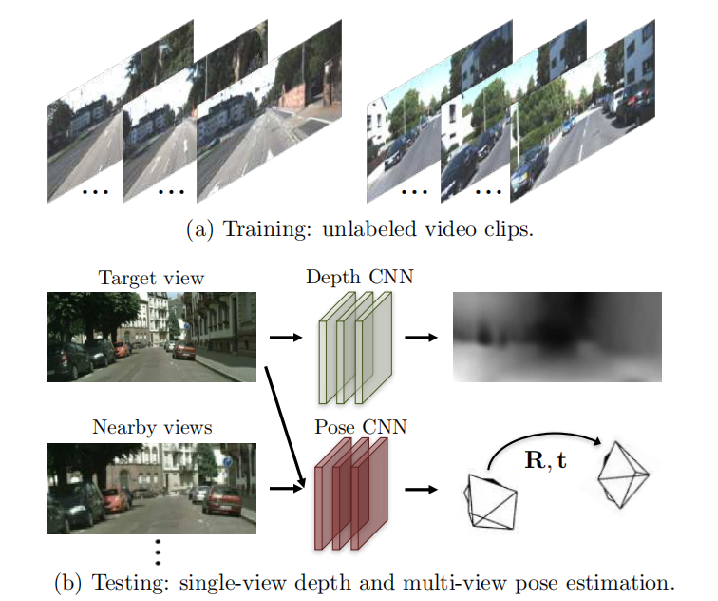
作者巧妙地利用SFM（Structure from motion）原理同时训练DepthNet（深度估计网络）和PoseNet（姿态估计网络），使用它们的输出重构图像$\hat I$与原图像$I$进行比较，免除真实深度label的需要。
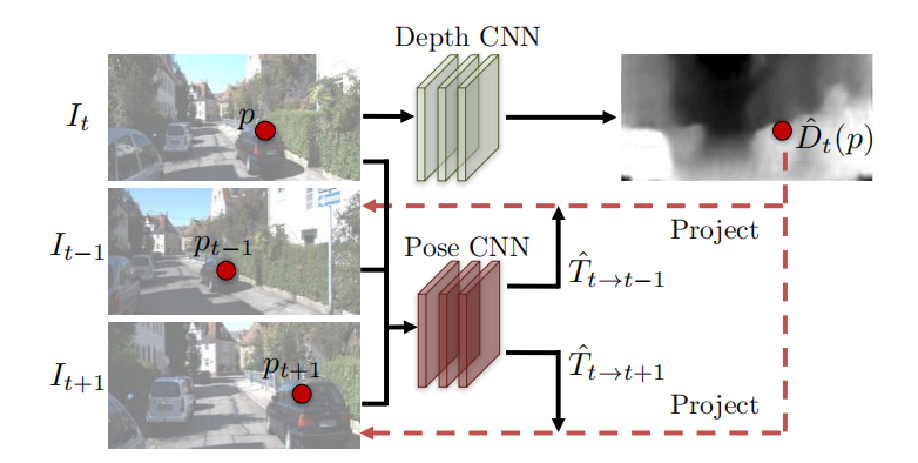
选择从时间上连续的三张图像，分别是$I_{t-1}$，$I_t$，$I_{t+1}$。DepthNet学习$I_t$的深度并输出深度图$\hat D_t$，PoseNet从$I_t$分别到$I_{t-1}$和$I_{t+1}$学习转换矩阵$\hat T_{t \to t-1}$和$\hat T_{t \to t+1}$，如上图，图像$I_t$里的$p$点可以通过对应的深度值$\hat D_t(p)$和转换矩阵$\hat T_{t \to t-1}$投影到$I_{t-1}$上对应位置$p_{t-1}$。
$p_s \sim K \hat T_{t \to s} \hat D_t(p_t)K^{-1}p_t$
其中，$K$是摄像头的内参矩阵（出厂时进行标定或自己标定）。
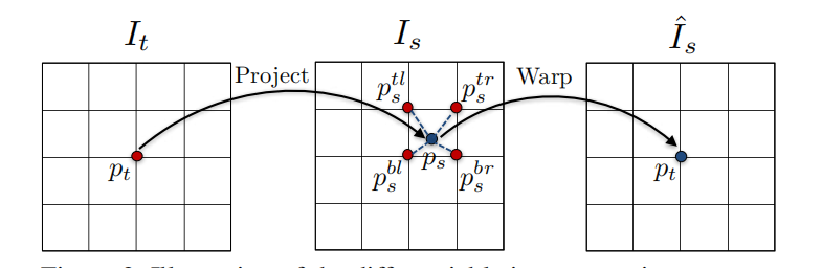
投影到的位置后使用相邻像素进行双线性插值进行图像重建，以光度重建缺失同时训练两个网络。
$L_{vs} = \sum_s{\sum_p | I_t(p) - \hat I_s(p)|}$
局限性
应用在视频时，方案包含了三个假设前提
1. 依赖于SFM，如果图像里的物体是“静止”，其实是该物体和本身的运动速度一致，那个该物体在不同时间上的视图里，不会发生变化，固“静止”。
2. 不考虑遮挡，是先把要处理的问题简单化。
3. 重建损失的前提。
局限性解决
1. 解决静止和遮挡
增加一个可解释性预测网络，该网络为每个目标-源对输出每个像素的软掩码$\hat E_s$，表明网络信任那些目标像素能进行视图合成。基于$\hat E_s$后的损失函数为
$L_{vs} = \sum_{<I_1,...,I_N> \in S}{\sum_p{\hat E_s(p)|I_t(p) - \hat I_s(p)|}}$
由于不能对$\hat E_s$直接监督，使用上述的损失进行训练将导致网络总是预测$\hat E_s$为零（就最小化了损失）。为了解决这个问题，添加一个正则项$L_{reg}(\hat E_s)$，通过在每个像素位置上使用常数标签1最小化交叉熵损失来鼓励非零预测。
2. 克服梯度局部性
上述的学习方式还有一个遗留问题，梯度主要来自$I(p_t)$和它4个邻居之间的像素强度差，如果像素位于低纹理区域或远离当前估计，则会抑制训练。解决这个问题有两个方案：
1. 使用总面积encoder-deconder架构，深度网络的输出隐含地约束全局平滑，并促进梯度从有意义的区域传播到附近的区域。
2. 明确的多尺度和平滑损失，允许直接从更大的空间区域导出梯度。
作者选择第二种方案，原因是它对架构选择不太敏感。为了平滑，作者最小化预测深度图的二阶梯度的L1范数。最终的损失函数为：
$L_{final} = \sum_l{L_{vs}^l} + \lambda_s L_{smooth}^l + \lambda_e \sum_s{L_{reg}(\hat E_s^l)}$
总结
在作者提出该方案前，已经存在基于深度值的监督学习和基于姿态的监督学习，他的出发点是以多种有相关性的任务同时学习，从而融合它们的学习结果可以回归到原图像，这使一方面同时训练多个相关模型，另一方面能起到自监督的效果。从这篇论文开始，单目深度估计进入自监督学习的阶段。
