四叉树 - pb2016

四叉树

小Ho：朴素的想法是我用一个二维数组来把整个平面图表示出来。假设坐标的范围是L，那么就需要一个L*L的数组。

对于(a,b)和r，我就检查a-r到a+r行的b-r列到b+r列，看其中是否存在有点，并且点到(a,b)的距离是小于等于r的。

对于L超过10000的情况就没有办法实现了。

小Hi：没错，在坐标范围和点数都很大的情况下，确实会有这样的问题。

小Ho：我在想能不能把整个区域分割成若干的小区域，每次都在附近的小区域去找临近的点呢。

小Hi：小Ho你这个想法很棒，我们不妨来试试吧？

小Ho：那应该怎么分割呢？

小Hi：你还记得线段树么？在线段树的处理中，我们将一个区间从中点分成两段。这里我们也用同样的方法，将一个区域分割为4块好了：

从上到下，从左到右，分别标记为1234。

我们将所有的点放进这些区域中，为了让一个区域中点数不过多，我们设定一个区域的点数上限。

若一个区域的点数过多，我们就将这个区域四分，把新的点放到子区域中去。

小Ho：听上去好像很有道理。

小Hi：当然有道理了，这种数据结构叫做"四叉树(Quadtree)"。其每个基本单元为：

QuadtreeNode:
	const NODE_CAPACITY; // 每个节点包含的点数限制，常量
	boundary; // 该节点的范围，包含4个参数，区域的上下左右边界
	points; // 该区域内节点的列表
	childNode; // 包含4个参数，分别表示4个子区域

假设NODE_CAPACITY=1，那么我们可以把整个区域分割为：

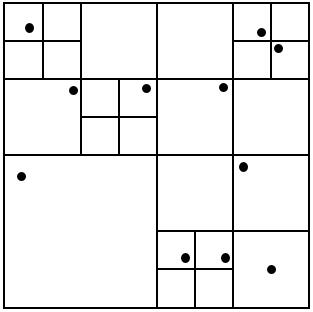
小Ho：恩，这个我理解了，因为跟线段树差不多，那么也就是同样存在插入和查询操作了？

小Hi：没错。

四叉树的插入操作：将新的节点(x,y)插入时，若不在当前区域内，退出；否则将其加入该区域的节点列表points，若当前区域的节点列表已经满了。那么将该区域进行四分，同时将节点加入子区域中。

insert(QuadtreeNode nowNode, point p):
	If (p not in nowNode.boundary) Then
		Return 
	End If
	If (nowNode.points.length < NODE_CAPACITY) Then
		nowNode.points.append(p)
	Else
		nowNode.divide() // 将区域四分
		For each childNode of nowNode
			insert(childNode, p)
		End For
	End If

四叉树的查询操作一般是求一个范围内的点，因此带入的参数也是一个区域range：

query(QuadtreeNode nowNode, range):
	If (QuadtreeNode.boundary does not intersect range) Then
		//该节点的区域与查询区域不相交
		Return empty
	End If
	For each p in nowNode.points
		If (p in range) Then
			pointsInRange.append(p)
		End For
	End For
	If (nowNode.isDivide) Then
		// 如果该区域有分割过，那么子区域中的节点也有可能在其中
		For each childNode of nowNode
			query(childNode, range)
		End For
	End If
	Return pointsInRange

题目：

描述

小Ho：下个周末我们打算去隔壁城市玩吧？

小Hi：反正来回也挺近的，好啊。

小Ho：那么我先来规划一下游玩路线吧。

小Ho打开了手机中的地图APP，把坐标移动到了隔壁的城市。各种各样的店铺显示在了街道的地图上。

小Hi：小Ho，你知道地图APP是怎么计算出你周围的店铺么？

小Ho：哎？没有想过哎。

小Hi：其实这也是个很有意思的问题呢。我们先把模型简化一下，假设有一张平面图，上面分布了N个点，第i个点的坐标为(x[i],y[i])。

小Ho：用点来代表店铺么？

小Hi：是的，然后假如我们所在的坐标为(a,b)，那么以我们为中心半径为r的范围内(包含边上)，有多少个点呢？

小Ho：感觉是个很有意思的问题呢，让我想一想。

提示：四叉树(Quadtree)

输入

第1行：2个整数N,M。1≤N≤50,000,0≤M≤5,000。

第2..N+1行：每行2个整数x,y，第i+1行表示第i个点的坐标，保证没有重复的点。0≤x,y≤30,000

第N+2..N+M+1行：每行3个整数a,b,r，表示询问的中心坐标(a,b)，以及半径r。0≤a,b,r≤30,000

输出

第1..M行：每行1个整数，第i行表示以第i个询问的(x,y)为中心所包含的点数。

样例输入

样例输出

1
2

ac代码：

  1 #include<cstdio>
  2 #include<cstring>
  3 #include<algorithm>
  4 #include<iostream>
  5 #include<cmath>
  6 using namespace std;
  7 
  8 struct Area{
  9     int l,r,t,d;
 10 };
 11 
 12 struct Point{
 13     int x,y;
 14 };
 15 
 16 struct Node{
 17     Node *lt,*rt,*ld,*rd;
 18     Area A;
 19     int ct;
 20     Node(Area a){
 21         lt=rt=ld=rd=NULL;
 22         A.l=a.l;
 23         A.r=a.r;
 24         A.t=a.t;
 25         A.d=a.d;
 26         ct=0;
 27     }
 28 };
 29 
 30 void inser(Node *&T,Area a,Point p){
 31     if (T==NULL) T=new Node(a);
 32     if ((T->A).l>p.x) return ;
 33     if ((T->A).r<p.x) return ;
 34     if ((T->A).d>p.y) return ;
 35     if ((T->A).t<p.y) return ;
 36     (T->ct)++;
 37     if (a.l==a.r&&a.t==a.d) return ;
 38     int x=(a.l+a.r)/2;
 39     int y=(a.t+a.d)/2;
 40     Area w;
 41     if (a.l==a.r){
 42         w.l=w.r=a.l;
 43         w.t=a.t;
 44         w.d=y+1;
 45         inser(T->lt,w,p);
 46         w.t=y;
 47         w.d=a.d;
 48         inser(T->ld,w,p);
 49     }
 50     else if (a.t==a.d){
 51         w.t=w.d=a.t;
 52         w.l=a.l;
 53         w.r=x;
 54         inser(T->lt,w,p);
 55         w.l=x+1;
 56         w.r=a.r;
 57         inser(T->rt,w,p);
 58     }
 59     else{
 60         w.l=a.l;
 61         w.t=a.t;
 62         w.d=y+1;
 63         w.r=x;
 64         inser(T->lt,w,p);
 65         w.l=x+1;
 66         w.t=a.t;
 67         w.d=y+1;
 68         w.r=a.r;
 69         inser(T->rt,w,p);
 70         w.l=a.l;
 71         w.t=y;
 72         w.d=a.d;
 73         w.r=x;
 74         inser(T->ld,w,p);
 75         w.l=x+1;
 76         w.t=y;
 77         w.d=a.d;
 78         w.r=a.r;
 79         inser(T->rd,w,p);
 80     }
 81 }
 82 
 83 int Find(Node *T,Point p,int r){
 84 
 85     if (T==NULL) return 0;
 86     if (T->ct==0) return 0;
 87     int flag=0;
 88     if (r*r-pow(p.x-(T->A).l,2)>=pow(p.y-(T->A).t,2)) flag++;
 89     if (r*r-pow(p.x-(T->A).l,2)>=pow(p.y-(T->A).d,2)) flag++;
 90     if (r*r-pow(p.x-(T->A).r,2)>=pow(p.y-(T->A).t,2)) flag++;
 91     if (r*r-pow(p.x-(T->A).r,2)>=pow(p.y-(T->A).d,2)) flag++;
 92     if (flag==0){
 93         if ((T->A).r<p.x-r) return 0;
 94         if ((T->A).l>p.x+r) return 0;
 95         if ((T->A).t<p.y-r) return 0;
 96         if ((T->A).d>p.y+r) return 0;
 97         if ((T->A).r<p.x){
 98             if ((T->A).d>p.y) return 0;
 99             if ((T->A).t<p.y) return 0;
100         }
101         if ((T->A).l>p.x){
102             if ((T->A).d>p.y) return 0;
103             if ((T->A).t<p.y) return 0;
104         }
105     }
106     if (flag==4) return T->ct;
107     return Find(T->lt,p,r)+Find(T->ld,p,r)+Find(T->rt,p,r)+Find(T->rd,p,r);
108 }
109 
110 
111 int main(){
112     Area a;
113     a.l=a.d=0;
114     a.r=a.t=30000;
115     Node *root;
116     root = new Node(a);
117     int n,m;
118     scanf("%d%d",&n,&m);
119     Point p;
120     while (n--){
121         scanf("%d%d",&p.x,&p.y);
122         inser(root,a,p);
123     }
124     while (m--){
125         int r;
126         scanf("%d%d%d",&p.x,&p.y,&r);
127         printf("%d\n",Find(root,p,r));
128     }
129 }

posted on 2016-11-13 14:26 pb2016 阅读(1394) 评论(0) 编辑收藏举报