协同过滤推荐(Collaborative Filtering Recommendation)
User-based CF: 基于User的协同过滤,通过不同用户对Item的评分来评测用户之间的相似性,根据用户之间的相似性做出推荐;
基于用户的协同过滤分为两个步骤:
1. 找到与目标用户兴趣相似的用户集合
2. 找到这个集合中用户喜欢的、并且目标用户没有听说过的物品推荐给目标用户
计算两个用户的兴趣相似度:
设 N(u) 为用户 u 喜欢的物品集合,N(v) 为用户 v 喜欢的物品集合:
Jaccard 公式:

余弦相似度:

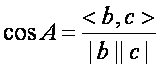

其中分母表示两个向量b和c的长度,分子表示向量的内积。

在本例中,用户A对物品{a,b,c}有过行为,用户B对物品{a,c}有过行为,利用余弦相似度公式计算用户A和用户B的兴趣相似度,以及A和C、D的相似度:

向量A = {1,1,0,1,0};
向量B = {1,0,1,0,0};

如果两两用户都利用余弦相似度计算相似度。这种方法的时间复杂度是O(|U|*|U|),这在用户数很大的情况下十分耗时。事实上,很多用户相互之间并没有相同的物品产生行为,即很多时候N(u)和N(v)的交集为0。那么,一种高效的算法就是首先计算出交集不为0的用户对{u,v},然后再对这种情况除以分母|N(u)UN(v)|(或者另一种根号形式)。
为此,可以首先建立物品到用户的 倒查表 ,对于每个物品都保存对该物品产生过行为的用户列表。令系数矩阵C[u][v]=|N(u)并N(v)|。那么,假设用户u和用户v同时属于倒排表中K个物品对应的用户列表,就有C[u][v]=K。从而,可以扫描倒查表中每个物品对应的用户列表,将用户列表中的两两用户对应的C[u][v]加1,最终就可以得到所有用户之间不为0的C[u][v]。
建立的倒查表:

建立一个4*4的 用户相似度矩阵W ,对于物品a,将W[A][B]和W[B][A]加1,对于物品b,将W[A][C]和W[C][A]加1,以此类推。扫描完所有物品后,我们可以得到最终的W矩阵。这里的W是余弦相似度中的分子部分,然后将W除以分母可以得到最终的用户兴趣相似度。

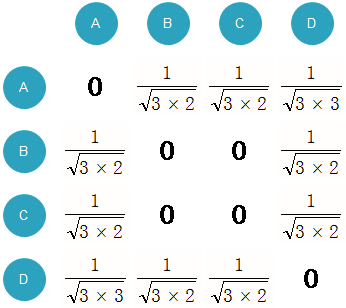
推荐物品:
首先需要从矩阵中找出与目标用户 u 最相似的 K 个用户,用集合 S(u, K) 表示,将 S 中用户喜欢的物品全部提取出来,并去除 u 已经喜欢的物品。对于每个候选物品 i ,用户 u 对它感兴趣的程度用如下公式计算:

其中 rvi 表示用户 v 对 i 的喜欢程度,在本例中都是为 1,在一些需要用户给予评分的推荐系统中,则要代入用户评分。
举个例子,假设我们要给 A 推荐物品,选取 K = 3 个相似用户,相似用户则是:B、C、D,那么他们喜欢过并且 A 没有喜欢过的物品有:c、e,那么分别计算 p(A, c) 和 p(A, e):


用户 A 对 c 和 e 的喜欢程度是一样的,在真实的推荐系统中,只要按得分排序,取前几个物品就可以了。





