| 先来复习一下概率论的基础知识： n 个数，从中取 m 个进行进行排列，有多少中排法。 如果不同位置可以重复： 第 1 个位置有 n 种选法 第 2 个位置有 n 种选法 ...... 第 m 个位置有 n 种选法 根据乘法原理：总共 n**m 种排法 如果不能重复 第 1 个位置有 n 种选法 第 2 个位置有 n-1 种选法 ...... 第 m 个位置有 n-m+1 种选法 根据乘法原理： 总共 n*(n-1)*....*(n-m+1)种排法 全排列就是 n! 种排法 |
如果我们要编程生成所有的排列，基本上都是嵌套循环
假如 list 有 n 个元素，从中选 2 个进行排列，伪代码基本如下
for i=0 to list.length-1
for j=0 to list.length-1{
//找到一种排列方法
temp=list[i,j]
//根据情况排除重复
..
}
for j=0 to list.length-1{
//找到一种排列方法
temp=list[i,j]
//根据情况排除重复
..}
问题是上面的例子，我们知道选 2 个元素排列，所以循环是 2 层。
但是，如果我们求得是 P(list,n)，n 并不确定，我们不知道循环是几层，要想写一个通用的函数，只能借鉴上面的思想，但是不能使用上面的形式
我的想法是：
1、用一个数组 repeat[] 来保存每层的循环变量：repeat[0] 保存第 0 层循环变量的位置，repeat[1] 保存第 1 层循环变量的位置......repeat[n-1] 保存第 n-1 层循环变量的位置
2、标记当前正在第几层循环：layer
3、集合长度已知 ：size = list.length
4、临时数组：temp[]，长度为 n
3、算法描述如下：
循环体（layer == 0 且 repeat[0]== size 则退出循环）
{
如果（前 n-1 层）
{
取出该层循环变量：pos=repeat[layer]
如果 (pos 到达该层末尾，即 pos==size)
{
temp[layer]=null
repeat[layer]=0//该层循环变量归零
layer--//回到上一层
continue
}
否则
{
temp[layer]=list[pos]
repeat_count[layer]++//该层循环变量增加1
layer++//层数增加 1
continue
}
否则（在最内层）
{
不停改变 temp 最后一个元素，每改变一次，就得到一种新的组合，该层循环变量增加1
当最内层也到达 List 末尾：将该层循环变量归零，回到上层
}
}
下面是我用 Python 编写的 permutation 函数，接受三个参数
第一个参数：如果数字则返回排列数；如果是集合，则返回排列的集合
第二个参数：选几个数排列，默认全排序
第三个参数：是否允许重复，默认不允许
例子：
print permutation(10),'\n' #全排列数
print permutation(10,2),'\n' #10 选 2 排列数
print permutation(10,duplicate=True),'\n' #允许重复的全排列
li=['a','b','c']
print '全排列：',permutation(li),'\n'
print '选2 ：',permutation(li,2),'\n'
print '允许重复 ：',permutation(li,duplicate=True),'\n'
print permutation(10,2),'\n' #10 选 2 排列数
print permutation(10,duplicate=True),'\n' #允许重复的全排列
li=['a','b','c']
print '全排列：',permutation(li),'\n'
print '选2 ：',permutation(li,2),'\n'
print '允许重复 ：',permutation(li,duplicate=True),'\n'
运行结果：
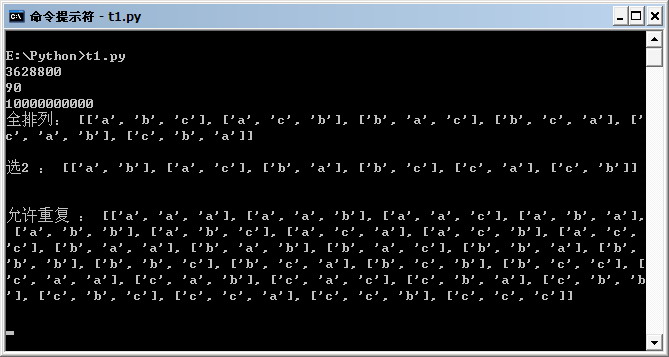
下面给出源代码：
排列
