题目：
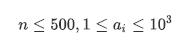
分析：
定义dp[ i ] [ j ]为原序列中第i个元素，在归并后放在了j这个位置的概率
最后的答案是概率乘上每一个可能的位置。
考虑怎么转移：
在归并排序中，遇到相同的就将对应的区间提出来，模拟两两相同元素比较的过程，统计贡献。
对于上一层的一个元素k，它通过一堆相同的比较后，放入位置 t 的概率是：C(t-1,k-1)/2^t
它原来位于位置k，就有k-1个元素在它前面，而它放入了位置t，要比较t次，所以是2^t 。
左边放的k-1个，总共放了t-1个，所以有C(t-1,k-1)的可能。
最后的答案就是枚举每一个元素的可能的位置以及期望去统计即可。
#include<bits/stdc++.h> using namespace std; #define ll long long #define N 505 #define mid ((l+r)>>1) #define ri register int const ll mod = 998244353; ll fac[N],invfac[N],inv2[N],f[N],dp[N][N],ans[N]; int a[N],b[N],c[N],n; ll quick_pow(ll a,ll k) { ll anss=1; while(k) { if(k&1) anss=anss*a %mod; a=a*a %mod; k>>=1; } return anss; } void init() { fac[0]=1; for(ri i=1;i<=n;++i) fac[i]=fac[i-1]*i %mod; invfac[n]=quick_pow(fac[n],mod-2); for(ri i=n;i>=1;--i) invfac[i-1]=invfac[i]*i %mod; inv2[1]=quick_pow(2,mod-2); inv2[0]=1; for(ri i=2;i<=n;++i) inv2[i]=inv2[i-1]*inv2[1] %mod; } ll C(int n,int m) { if(n<m) return 0; return fac[n]*invfac[n-m] %mod *invfac[m] %mod; } void work(int l1,int r1,int l2,int r2)//统计概率 { for(ri j=l1;j<=r1;++j){//枚举左区间每一个点统计贡献 for(ri k=1;k<=r1-l1+1;++k){//枚举左边的第k个元素放入t这个位置 for(ri t=k;t<=r2-l2+k;++t)//枚举这个点k放在下一个序列里面的位置t f[t]=(f[t] + dp[b[j]][k]*C(t-1,k-1) %mod *inv2[t] %mod) %mod;//计算：C(t-1,k-1)/2^t //特殊处理左边的全部放入，右边只能顺着放的情况，那么右边顺着放就不会产生贡献 for(ri t=r2-l2+1;t<=r2-l2+k;++t)//这里的t枚举的是右边全部放完 最后一个位置放的地方 //因为只有知道它放的地方 才知道从哪里开始已经不产生贡献 f[r2-l2+1+k]=( f[r2-l2+1+k] + dp[b[j]][k]*C(t-1,r2-l2) %mod *inv2[t] %mod) %mod; //因为k固定，右区间放多少元素也固定 所以这里的r2-l2+1+k是固定的 } for(ri k=1;k<=r1-l1+1+r2-l2+1;++k) dp[b[j]][k]=f[k],f[k]=0;//用f临时记录，可以减少一维dp，减少了层数那一维 } for(ri j=l2;j<=r2;++j){//和上面的一样 for(ri k=1;k<=r2-l2+1;++k){ for(ri t=k; t<=r1-l1+k; ++t) f[t]=(f[t] + dp[b[j]][k]*C(t-1,k-1) %mod *inv2[t] %mod ) %mod; for(ri t=r1-l1+1; t<=r1-l1+k; ++t) f[r1-l1+1+k]=( f[r1-l1+1+k] + dp[b[j]][k]*C(t-1,r1-l1) %mod *inv2[t] %mod ) %mod; } for(ri k=1;k<=r1-l1+1+r2-l2+1;++k) dp[b[j]][k]=f[k],f[k]=0; } } void merge_sort(int l,int r) { if(l==r) { dp[b[l]][1]=1; return ; }//自己在自己本来的位置 概率是1 merge_sort(l,mid); merge_sort(mid+1,r); int p=l,q=mid+1; for(ri i=l;i<=r;++i){ if(p<=mid && a[b[p]]<a[b[q]] || q>r) c[i]=b[p++]; else if(q<=r && a[b[p]]>a[b[q]] || p>mid) c[i]=b[q++]; else{ int l1=p,r1=p,l2=q,r2=q; while(r1<mid && a[b[r1+1]]==a[b[l1]]) r1++; while(r2<r && a[b[r2+1]]==a[b[l2]]) r2++; work(l1,r1,l2,r2);//找到左边连续的一段 和 右边连续的一段 当合并他们的时候要统计贡献 for(ri k=l1;k<=r1;++k) c[i]=b[k], i++; for(ri k=l2;k<=r2;++k) c[i]=b[k], i++; i--; p=r1+1; q=r2+1; } } for(ri i=l;i<=r;++i) b[i]=c[i]; } int main() { freopen("sort.in","r",stdin); freopen("sort.out","w",stdout); scanf("%d",&n); for(ri i=1;i<=n;++i) scanf("%d",&a[i]),b[i]=i;//不能对a直接排序，将a的下标b拿去排序 init(); merge_sort(1,n); for(ri l=1,r;l<=n;l=r+1){ r=l; while(r<n && a[b[r+1]]==a[b[l]]) r++;//跳连续的相同区间统计贡献 for(ri i=l;i<=r;++i)//这一段相同的里面 每一个数都有其可以放的位置 位置再乘上概率就是期望 for(ri j=1;j<=r-l+1;++j) ans[b[i]]=( ans[b[i]] + dp[b[i]][j]*(j+l-1) %mod ) %mod;//bi是i这个元素 在原来数组中的下标 这时的dp是最后一层的dp } for(ri i=1;i<=n;++i) printf("%lld ",ans[i]); return 0; }
